$\def\ket#1{\mid #1\rangle}$
1. Security System of the Classical Computer
Quantum computers can show amazing performance for not only speed but also security.
Exaggeratedly speaking, it has a “theoretically perfect security system”.
Security System of the Classical Computer
There is a simple and famous example when handling the security problem: ABE situation. Alice(A) wants to send some messages to Bob(B), but Eve(E) tries to steal the messages.
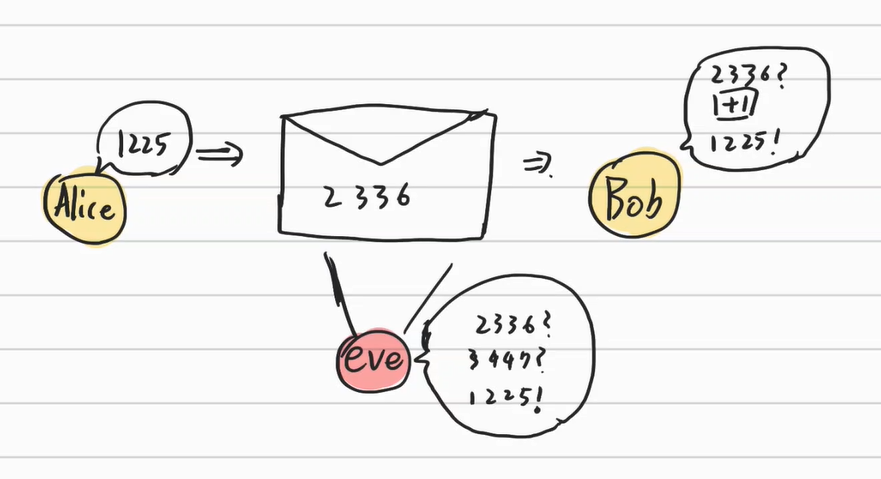
For example, suppose that Alice is going to send a message “1225” to Bob to see him at Christmas. Alice is going to write 1225 on a paper, but she is worried that her rival Eve will steal the message. Therefore, Alice sends the message in a way that Bob can understand but Eve cannot.
The most general way is sharing the way to interpret the message with Bob. For example, encode 1225 as 2336 with addition 1 to each element. If Bob knows the encoding method, he can easily interpret the message but Eve cannot interpret it.
This way, the information shared by the communication party is called a Key. This procedure is used more or less for almost every cryptography.
But there is a problem with this method. If Eve is an expert on cryptography, then she can infer the method of encoding and can interpret the message.
RSA Cryptosystem (Rivest/Shamir/Adlemam cryptosystem)
Therefore, we need some problems hard to be inferred for outsiders but easy to be solved for the party. This can be called an NP-hard problem. NP-hard problem is a concept used at Algorithm which means that the problem needs exponential time to derive some solutions but takes polynomial time to confirm the solutions. The simplest and hardest problem which meets the conditions is a factorization problem. In general, it is hard to find the factor but easy to confirm it.
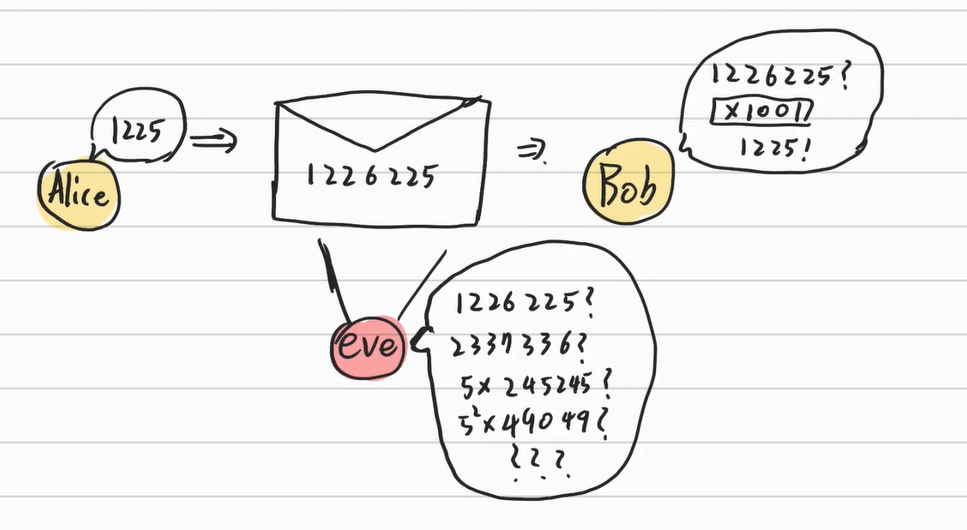
For example, when Alice send the number 1225, they can share a specific number like 1001 and multiply it to the message. In this time, Alice will send the number $1226225(1225\times 1001)$. Bob can understand the number intended by Alice is 1225 by dividing 1226225 with 1001.
To figure out the number 1001, Eve has to do factorization. She has to see the result of dividing the number with prime numbers and examine whether the remainder is zero or not and it takes a lot of time. When the problem becomes complex, then it is almost impossible to solve the problem.
In reality, people use a much more complex system based on the RSA system so they protect the message with multiple layers .
2. The Cryptosystem of the Quantum Computer.
Adverse of the Quantum Computer and Neutralization of RSA cryptosystem
The RSA system can be neutralized when the quantum computer becomes commercialized. It is because the quantum computer can solve the factorization problem in polynomial time.
According to the research of Dr. John Martinis in UCSB, to factorize the 2048 bit number, we have to invest $1,000,000 Trillion to make a super computer which is as large as the entire North America and uses 1 Trillion GW for ten years. (Contemporary annual electricity products of world is 3000 GW)
Meanwhile, if we use the quantum computer, we have to invest $100 billion to make a 1cm chip storing 10 million qubit and spend 0.01GW for 16 hours. It takes 0.000001% of money and 0.0003% of electricity and an incomparable size of space.
Therefore, most of the RSA cryptosystem based on the factorization can be destroyed. Fortunately, there is a substitute in the quantum algorithm.
The cryptosystem of the Quantum Computer
Like the classical cryptosystem, quantum systems also share some keys. The shared key is not numbers but the direction of measurement. By the direction of the qubit and measurement, the interpretation is changed. (Reference- https://hgmin1159.github.io/quantum/quantum1_eng/)
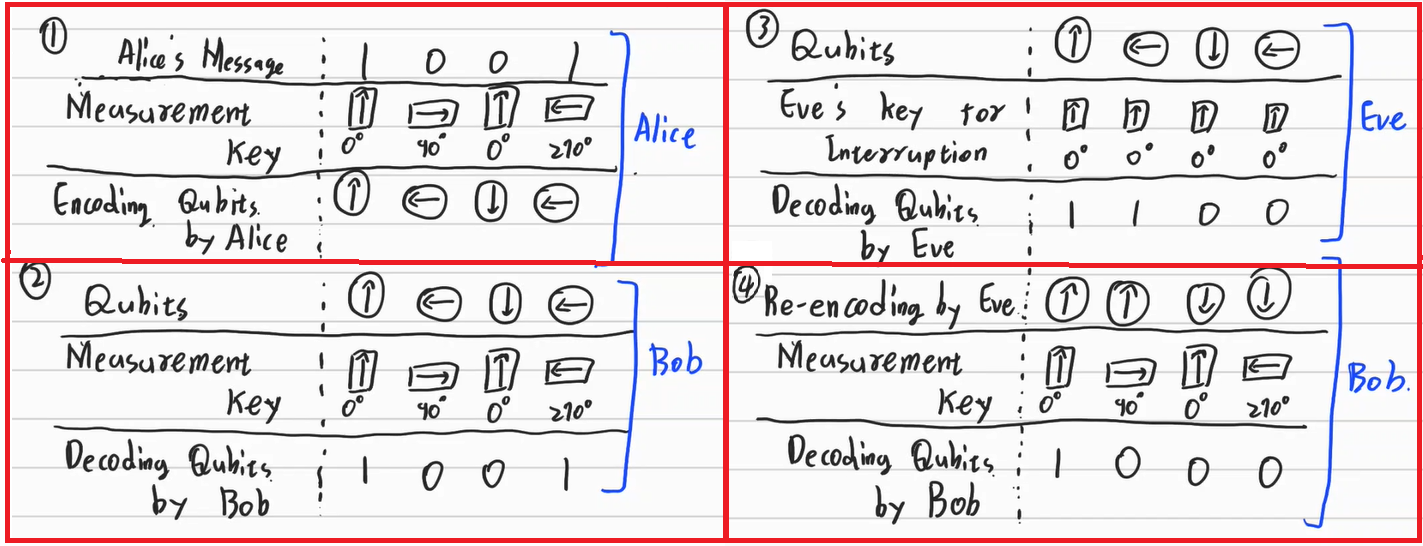
First of all, let’s assume Alice wants to deliver binary numbers 1001 to Bob. Alice and Bob share some measurement directions as 0’,90’,0’,270’. Alice encodes her value with predetermined directions. (figure-1)
Bob can interpret the number with shared key and can know the Alice’s number is 1001(figure-2)
Assume that Eve wants to steal the message. Eve has to interpret the qubit with her own key. Suppose that Eve measures the qubit with the direction of 0’,0’,0’,0’. Of course, Eve cannot interpret the number because it is different from the Alice’s one. (figure-3)
The important difference between the classical computer and quantum computer is, Eve distorts the entire message which Alice wants to deliver to Bob. Therefore, Eve cannot reverse the state of qubit before she measures them. (figure-4)
The advantages of this system are as follows.
- Infinitely many cases - we have seen the measurement key of 0,90,180,270 but the measurement degree can be any number between 0~360. If we consider the dimension and entanglement, then the fidelity of the number can be more. The number of the key means when solving the cryptosystem, Eve has to consider the cases as many as the number.
- Restricted Trial - In classical cryptography, people can do some trial and error to capture the exact key. This means that they can try to divide some numbers with prime numbers several times. However, in the quantum computer, they cannot do that because the whole information would disappear with just one trial.
- Capture the interference of 3rd person - If 3rd person tries to do interference, then the information becomes directly distorted. This means that we cannot see origin information and Alice and Bob can directly know that someone else tries to steal their messages.
With the above advantage, we can say that quantum computers cannot be hacked theoretically. Of course the above procedure is not realized yet and there might be a lot of obstacles to deal with problems.
3. Quantum Protocol
Exchanging quantum information between quantum computers is not yet practical. Therefore, there are detours to exchange the information. Most famous one of them is Superdense Code and Quantum Teleportation which are called Quantum Protocol.
Superdense Code
Superdense Code is an algorithm to deliver two bit by delivering one qubit.
Basic code of the superdense code is above.
Phase 1.
-
First input $\ket{q_0q_1}$ is $\ket{00}$. By passing these qubits to Bell’s circuit, we can make totally entangled qubits.
$\ket{00} \Rightarrow \frac{1}{\sqrt 2}(\ket{0}+\ket{1})\otimes\ket{0} \Rightarrow \frac{1}{\sqrt{2}}(\ket{00}+\ket{11})$
-
And Alice and Bob share these qubits one by one.
Phase 2.
- Alice can deliver the information by manipulate the qubit
The total information represented by one qubit is 2 bits and it is one of the 00,01,10,11. Below table shows manipulating gates and its corresponding result bits.
| Gate | Result bit |
|---|---|
| I | 00 |
| X | 01 |
| Z | 10 |
| Z - X | 11 |
If we pass through X, then qubit turns to follow.
$ \frac{1}{\sqrt{2}}(\ket{00}+\ket{11}) \Rightarrow \frac{1}{\sqrt{2}}(\ket{10}+\ket{01})$
Phase 3.
- Bob then passes inverse Bell’s circuit with a shared qubit and his own qubit. In this time, the qubit becomes as follows.
$\frac{1}{\sqrt{2}}(\ket{10}+\ket{01}) \Rightarrow \frac{1}{\sqrt{2}}(\ket{11}+\ket{01}) \Rightarrow \ket{01}$
Phase 4.
- If we measure such qubit, then we can get 01 with 100%
If we use this circuit, then we have to deliver N qubits to deliver 2N bits
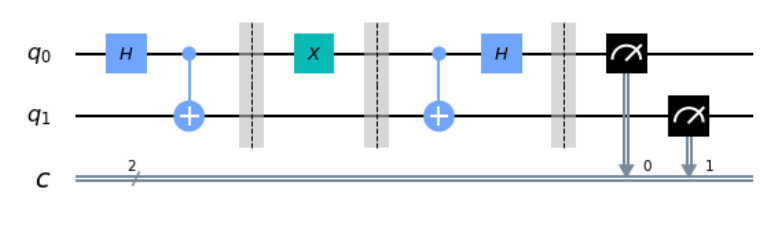
We can do them in actuality by using qiskit and python like below.
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
circ = QuantumCircuit(2,2)
circ.h(0)
circ.cx(0,1)
circ.barrier()
circ.x(0)
circ.barrier()
circ.cx(0,1)
circ.h(0)
circ.barrier()
circ.measure([0,1],[0,1])
circ.draw(output='mpl',justify='none')
Circuit is above. If we learn the circuit at the QASM simulator, then we can get the following result.
job_result = execute(circ, Aer.get_backend('qasm_simulator'))
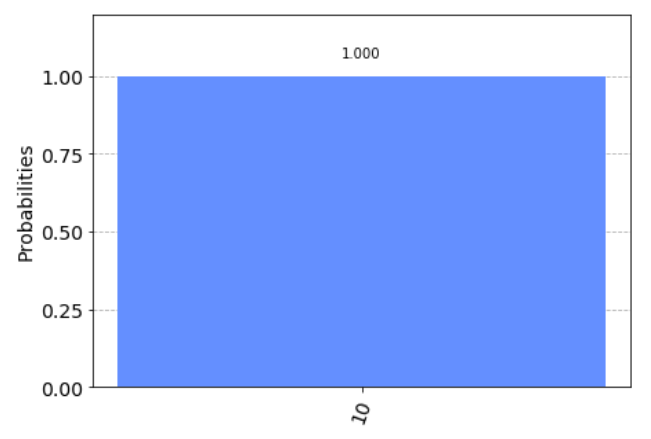
plot_histogram(job_result.result().get_counts(circ))
We can see that it returns 10 with 100%
Quantum Teleportation
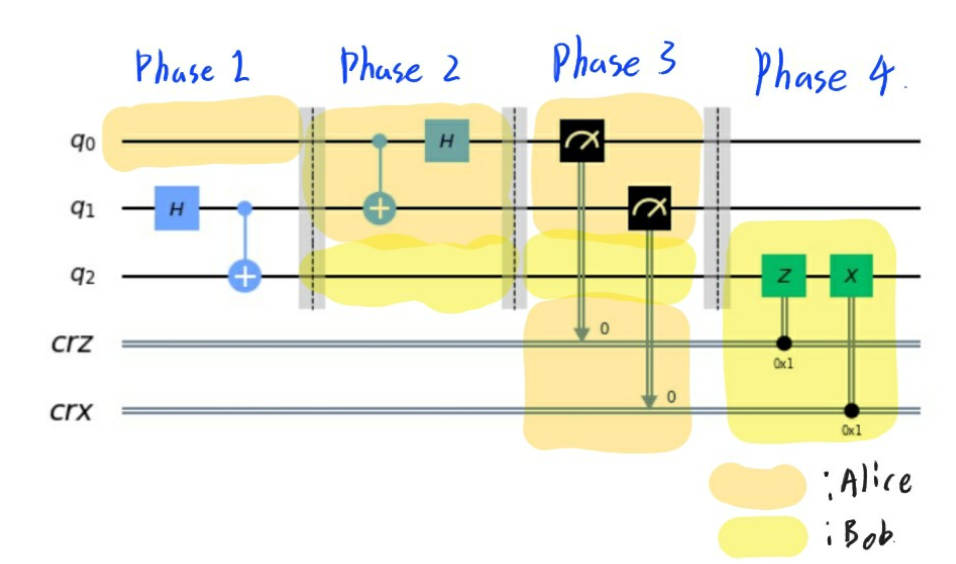
Quantum Teleportation is an algorithm to deliver the qubit of Alice to Bob. It has following circuit
Phase 1
-
$\ket{q_0}$ is the target qubit that Alice wants to deliver. Let’s represent it as follow $\ket{q_0} = a\ket{0}+b\ket{1}$
-
Alice and Bob share two perfectly entangled qubits with each other as follows.
$\ket{q_0}\otimes\ket{00} \Rightarrow \ket{q_0}\otimes\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{0} \Rightarrow \ket{q_0}\otimes\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})$
Phase 2
- Alice passes her qubit and shared qubit into inverse Bell’s circuit. In this time, the following qubit is below.
$\ket{q_0}\otimes\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})\ \Rightarrow \frac{a}{\sqrt{2}}\ket{0}\otimes(\ket{00}+\ket{11})+\frac{b}{\sqrt{2}}\ket{1}\otimes(\ket{11}+\ket{01})\ \Rightarrow \frac{1}{2}[\ket{00}(a\ket{0}+b\ket{1})+\ket{01}(b\ket{0}+a\ket{1})+\ket{10}(a\ket{0}-b\ket{1})+\ket{11}(-b\ket{0}+a\ket{1})]$
- In this time, the hadamard gate makes the qubit as follows.
$\ket{0} \rightarrow \frac{1}{\sqrt 2}(\ket{0}+\ket{1}),\ket{1} \rightarrow \frac{1}{\sqrt 2}(\ket{0}-\ket{1})$
Phase 3
- Alice sends the result of measuring the qubit to Bob. If the result is 00, then Bob have to takes I gates to $\ket{q_2}$ and if 01 then X, if 10 then Z and if 11,then takes ZX gates to $\ket{q_2}$
- That is, if the result is 00, then Bob’s qubit is $(a\ket{0}+b\ket{1})$, so remain unchanged and if it is 01, then Bob’s qubit is $(b\ket{0}+a\ket{1})$, so takes X gate.
- With above procedure, Bob can change his qubit into $\ket{q_0} = a\ket{0}+b\ket{1}$
Let’s do this.
To implement it, we need the c_if method. To use them we have to use the ClassicalRegister() function as below.
from qiskit import QuantumRegister, ClassicalRegister
qr = QuantumRegister(3, name="q")
crz = ClassicalRegister(1, name="crz")
crx = ClassicalRegister(1, name="crx")
And then let’s make a random state as below. There is a function in qiskit to experiment.
from qiskit_textbook.tools import random_state
from qiskit.extensions import Initialize
from qiskit.visualization import plot_bloch_multivector
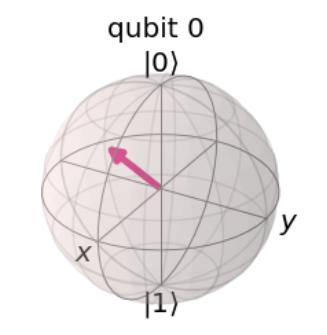
psi = random_state(1)
init_gate = Initialize(psi)
init_gate.label = "init"
plot_bloch_multivector(psi)
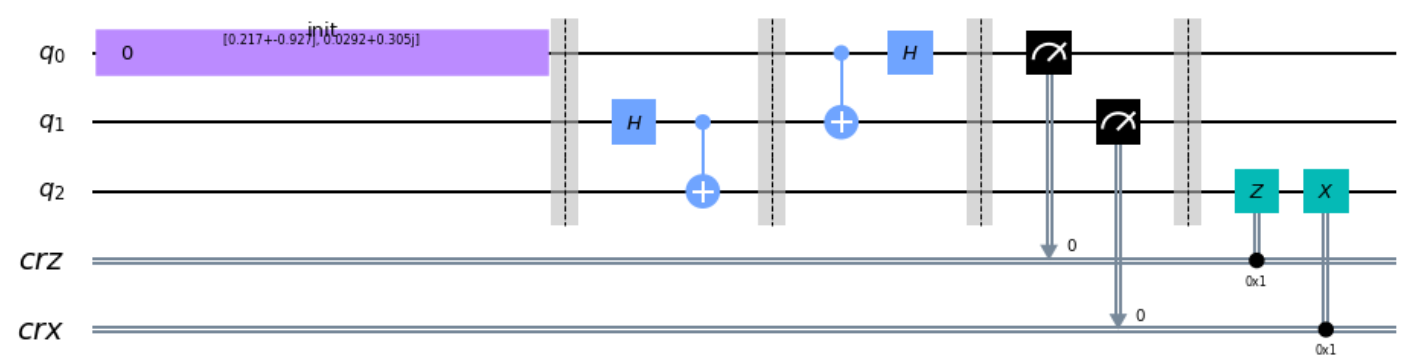
Now let’s make a circuit with them.
circ = QuantumCircuit(qr,crz,crx)
circ.append(init_gate, [0])
circ.barrier()
circ.h(1)
circ.cx(1,2)
circ.barrier()
circ.cx(0,1)
circ.h(0)
circ.barrier()
circ.measure(0,crz)
circ.measure(1,crx)
circ.barrier()
circ.z(qr[2]).c_if(crz,1)
circ.x(qr[2]).c_if(crx,1)
circ.draw(output='mpl',justify='none')
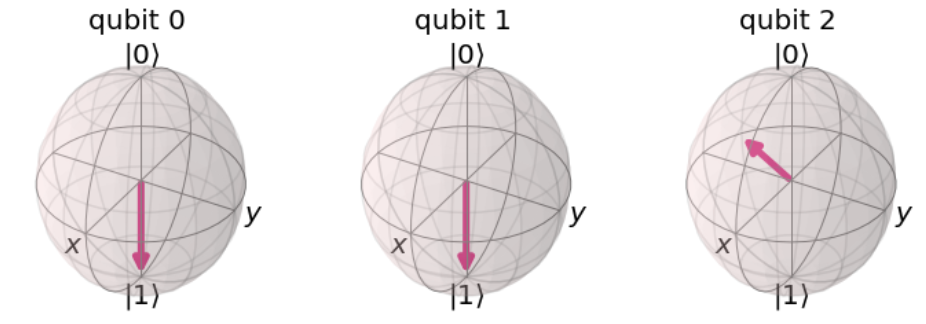
We need a Statevector Simulator to check the state of the qubit. And let’s use the Bloch sphere to see the exact state of it.
backend= Aer.get_backend('statevector_simulator')
result = execute(circ, backend).result()
psi = result.get_statevector()
plot_bloch_multivector(psi)
We can see that the state of the third qubit is exactly the same as the state of the first random qubit.
Sutor, R. (2019). Dancing With Qubits. Birmingham,UK:Packt
Bernhardt, C. (2019). Quantum computing for everyone. Boston, Massachusetts:The MIT Press