$\def\ket#1{\mid #1 \rangle}$
1. 양자 알고리즘의 기본
고전 컴퓨터에 비해 양자 컴퓨터가 빠른 이유는 하드웨어가 아니라 소프트웨어인 양자 알고리즘에서 기인한다. 그런데 거의 대부분의 양자 알고리즘은 확률증폭을 이용해서 문제를 풀어낸다. 이번 포스팅에서는 이 확률증폭에 대해서 알아보고 몇가지 기본적인 양자알고리즘에 대해서 적어보려고 한다.
a. 오라클(Oracle)
오라클(Oracle)은 함수의 일종으로 고대 그리스의 신탁에서 따온 명칭이다.
오라클은 입력값으로는 숫자나 문자 등 어떤 것이든 정해줄 수 있지만 출력값은 오직 1과 0만 반환해주는 함수이다. 이때, 1과 0은 Boolean Function의 일종으로 보아 True나 False를 반환한다고도 해석할 수 있다.
오라클을 다룰때는 함수가 입력값을 어떠한 처리를 해준 후에 1과 0을 반환하는 지에 대해서는 관심이 없다. 결과는 알지만 과정은 알지 못하는 것이다. 따라서 오라클을 블랙박스(Black Box)라고도 부른다.
또한, 컴퓨터에서는 모든 것을 1과 0의 bit로 처리할 수 있으므로 결국에는 다음과 같은 형태를 가질 것이다.
Oracle $f : {0,1}^n \rightarrow {0,1}$
양자 컴퓨터에서는 모든 연산은 Unitary Matrix하에서 이뤄진다. 따라서 이러한 오라클 함수도 Unitary Matrix의 형태로 표현된다. 구체적으로 다음을 만족하도록 짜여진다.
$U_f(\ket x) = \begin{cases} -\ket x \quad \mbox{ if } f(\ket x) = 1 \\ \ket x \qquad \mbox{ if } f(\ket x) = 0 \end{cases}$
이는 결과물의 확률 진폭만 Flip 시켜준다고 말할 수 있다.
예를 들어 다음과 같다.
3 큐빗짜리 큐빗을 생각해보자.
$\ket \psi = a_1\ket{000} + a_2 \ket{001} + a_3 \ket{010} + a_4 \ket{100} + a_5 \ket{011} + a_6 \ket{101} + a_7 \ket{110} + a_8 \ket{111}$
여기서 만약 오라클이 $\ket{010}$만 1로 반환하고 나머지는 0으로 반환할시 이에 대한 Unitary Matrix는 다음을 만족시켜주면 된다.
$\ket \psi = a_1\ket{000} + a_2 \ket{001} - a_3 \ket{010} + a_4 \ket{100} + a_5 \ket{011} + a_6 \ket{101} + a_7 \ket{110} + a_8 \ket{111}$
우리의 목표는 오라클이 True라고 말하고 있는 큐빗 상태($\ket 3 = \ket {010}$)를 모른다고 가정하고 찾아내는 것이다. 이때 목표로 해야하는 것이 바로 확률증폭이다.
b.확률증폭
$\psi$가 다중 Hadamard Gate(Kronecker Gate)를 통해 모든 상태가 나올 확률이 동일한 큐빗이라고 생각해보자.
즉 $\ket \psi = \sum_{j=1}^{8} \frac{1}{\sqrt 8} \ket j$이다.
이를 $U_f$에 통과시키면 다음과 같다.
$U_f \ket \psi = \frac{1}{\sqrt 8}\ket{000} +\frac{1}{\sqrt 8} \ket{001} - \frac{1}{\sqrt 8} \ket{010} + \frac{1}{\sqrt 8}\ket{100} +\frac{1}{\sqrt 8} \ket{011} + \frac{1}{\sqrt 8} \ket{101} + \frac{1}{\sqrt 8} \ket{110} + \frac{1}{\sqrt 8} \ket{111}$
이때 각 상태가 나올 확률은 같다. 하지만 베이시스(측정 방향)를 바꿔줌으로써 $\ket{010}$이 나올 확률만 증폭시켜줄 수 있다. 이를 진폭 증폭이라고 부르며 영어로는 amplitude amplification이다. (진폭 증폭은 직관적이지 않으므로 임의로 확률 증폭으로 부르자.)
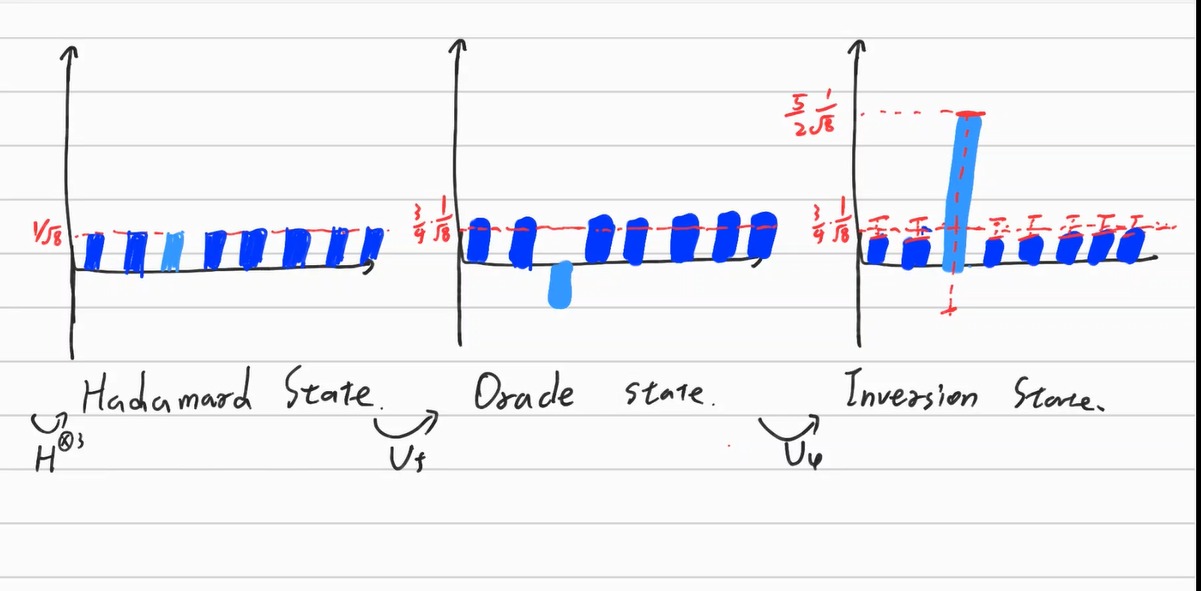
이에 대한 여러가지 테크닉이 있지만 이 경우에는 “inversion about the mean” 테크닉을 사용해 줄 수 있다.
Inversion about mean은 말그대로 평균을 중심으로 대칭이동 시켜주는 것이다. 8개의 확률진폭을 각각 평균 대칭이동 시켜줄 경우 혼자 확률진폭이 음수로 변한 $\ket {010}$만 매우 높아지게 되며 다른 것이 나올 확률은 극도로 낮아지게 된다. 아래의 그림을 살펴보자.
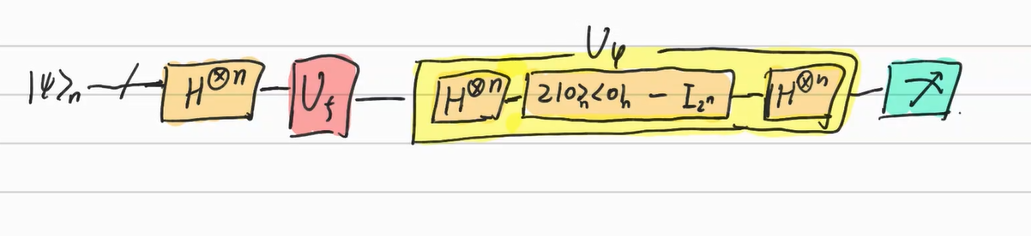
이 확률증폭을 시켜주는 Operator $U_\psi$는 다음과 같다.
$U_\psi = 2\ket \psi \langle \psi \mid - I_{2^n} \quad (\ket \psi \mbox{ is hadamard state}) \\ \quad = H^{\otimes n} (\mid 0 \rangle^{\otimes n} \langle 0 \mid ^{\otimes n} - I^{\otimes n})H^{\otimes n}$
이를 Grover diffusion operator라고 말한다.
결론적으로 다음과 같다.
이는 확률이 증폭되는 가장 간단한 예시라고 말할 수 있다.
이를 적절하게 짜면 좀 더 실용적인 예시들에 적용할 수 있다.
2. Grover’s Searching Algorithm
고전 컴퓨터의 검색 알고리즘
이러한 확률증폭은 컴퓨터의 다양한 분야에서 사용할 수 있다. 그 중 한 분야는 검색이다. 우선 고전 컴퓨터에서 저장된 데이터를 찾을때 어떤 알고리즘으로 진행되는 지에 대해서 알아보자.
100개의 상자에 초콜릿이 들어있다고 생각해보자. 그 중 한 군데에는 민트 초콜릿이 들어있고 나는 이 민트 초코를 찾아서 먹고 싶다. 상자를 하나씩 열어보는 상황을 가정할때, 시간이 가장 적게 걸리는 케이스는 처음 연 상자에 민트 초코가 들어 있을 때이고, 시간이 가장 많이 걸리는 케이스는 99개를 열어도 들어있지 않아 마지막 상자에 초코가 들어있는 경우이다.
따라서 최소 1번, 최대 100번의 시간이 걸린다. 이를 일반화하면 상자의 집합을 S, 이 집합의 크기를 n이라고 두며 검색의 시간 복잡도 함수는 $O(n)$이라고 말할 수 있다. 각각의 상자를 연 후 이 데이터가 필요로 하는 데이터인지 아닌지에 대한 검정이 필요하며 이것을 수행하는 것이 곧 오라클이라고 말할 수 있다. 즉, 오라클 f를 최소 n번 수행하는 것이라고 말할 수 있다.
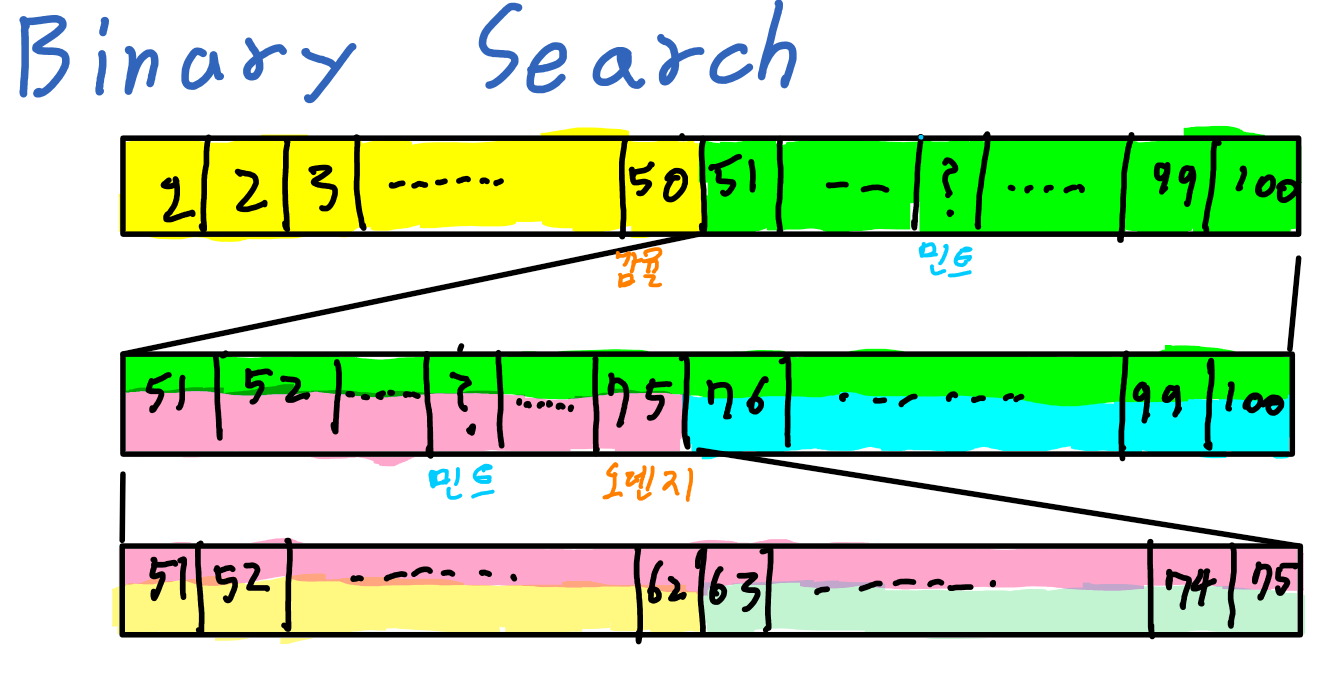
만약 이 상자의 집합에 대한 추가적인 정보가 있다면 좀 더 빠른 시간내에 찾을 수 있다. 예컨데 상자들이 초콜릿의 이름 순으로 정렬되어 있다고 가정하자. 100개의 상자 중 중간인 50번째 상자를 열어 봤을때 들어있는 초콜릿이 감귤 초콜릿 이면 감귤<민트 이므로 민트 초콜릿은 51~100번째에 들어있다고 생각할 수 있다.
그 다음 51~100번째의 75번째 상자를 열어봤을때 오렌지 초콜릿이 있었다면 민트<오렌지 이므로 민트 초콜릿은 51~75번째에 있다고 생각할 수 있다. 이런 방식으로 상자를 두개씩 분류해서 찾아나가는 기법을 Binary Search라고 말한다. 이 경우 $m-1< \log_2 n < m$ 인 m만큼의 상자를 열어보면 되므로 시간 복잡도 함수는 $O(\log n)$이다. 이 경우 정렬이 되지않은 데이터 셋에 비해 Exponentialy Improvement가 있다고 말하며 따라서 효율이 매우 높다고 말할 수 있다. 그러나 정렬이 되어있어야 한다는 전제조건이 있으므로 Binary Search가 사용이 불가능한 경우가 존재하기 마련이다.
그런데 Grover가 개발한 양자컴퓨터의 검색 알고리즘은 정렬이 되지 않은 열에 대해서 $O(\sqrt n)$만큼의 효율을 보인다. 이는 Quadratic Improvement라고 말하며 Exponentially Improvement만큼은 아닐 지라도 효율이 매우 높다고 말할 수 있다. 이에 대해서 구체적으로 알아보자.
Grover’s Algorithm
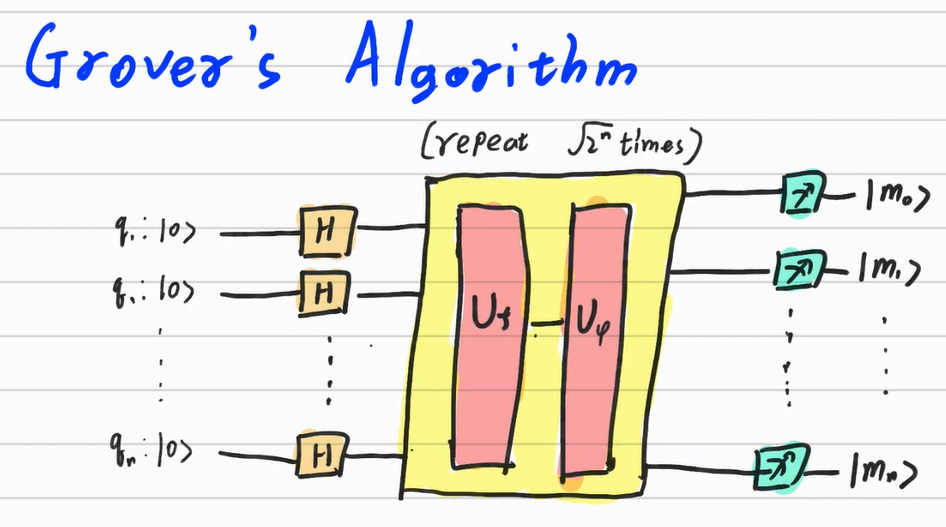
Grover’s Algorithm의 대략적인 과정은 다음과 같다.
- 집합 S의 크기 N을 파악하여 $2^{n-1} \leq N\leq2^n$인 n을 찾자.
- 찾고자 하는 Basis Ket의 확률 진폭을 뒤집는 오라클 행렬 $U_f$를 설계하거나 가져오자. 이는 사전에 주어질 수도 있고 데이터베이스에서 추출할 수도 있다.
- $U_fU_\psi$를 $\sqrt {2^n}$번 시행한 후 측정하자. 측정된 상태가 찾고자 하는 데이터의 위치를 의미한다.
-
일반적인 Searching Algorithm은 상자에서 꺼낸 후 데이터가 원하는 데이터인지 아닌지에 대한 검정, 즉 각각의 상자마다 오라클을 시행해야 했다면 Grover’s Algorithm은 상자 전체 (케이스 전체)에 대해 한꺼번에 오라클을 시행해본 후($ U_f$) 결과물을 확인하는 것이라고 말할 수 있다.
-
사실 1번에서 소개한 확률증폭에 대한 알고리즘을 여러번 시행한 것이다. 여러번 시행한 이유는 1번의 케이스에서는 큐빗이 3개이고 상태가 8개이므로 한번의 시행으로도 확률이 비교적 빠르게 수렴했지만 127:1,255:1 같은 케이스에서는 한번으로는 부족하기 때문이다.
-
결과물로 나온 큐빗이 데이터의 위치를 의미한다. 물론 확률이 0이 아닌 이상 오류는 존재하며 오류의 확률은 $O(\frac{1}{N})$이다.
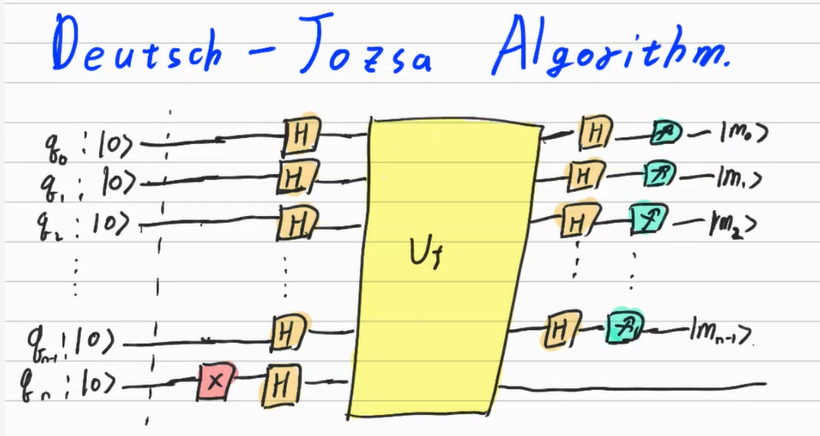
3. Deutsch - Jozsa Algorithm
Deutsch(도이치) 알고리즘은 퀀텀 컴퓨터의 초창기에 제안된 알고리즘이다. 비록 실용성은 떨어지지만 양자컴퓨터를 이용해 고전 컴퓨터보다 천문학적으로 앞서는 효율을 낼 수 있음을 보여준 첫번째 사례이기도 하다. Deutsch - Jozsa Algorithm(도이치 - 조자 알고리즘)은 이 Deutsch Algorithm을 다중 큐빗으로 확장시킨 사례이다.
이 알고리즘이 푸는 문제는 다음과 같다.
함수 $f:{0,1}^n \rightarrow {0,1}$는 Balanced 함수인가? Constant 함수인가?
Balanced 함수라고 함은 정의역 원소의 절반은 0으로, 나머지는 1로 맵핑되는 함수를 의미하고, Constant 함수라 함은 모든 정의역이 1 혹은 0 으로 매핑되는 함수를 의미한다. 이 또한 오라클의 일종으로 볼 수 있다.
고전 컴퓨터에서 인풋의 총개수 $2^n$개에 대해서 확인할때 최고의 경우에는 첫번째 시행에 0이 나오고 두번째 시행에서 1이 나와 constant가 아님을 바로 알게되는 경우이다. 반대로 최악의 경우에는 $2^{n-1}$까지 시행에서 모두 0 혹은 1이 나와 $2^{n-1}+1$번째 시행에서야 balance인지 constant인지 확인할 수 있는 경우이다. 물론 함수가 constant일때는 무조건 $2^{n-1}+1$번째 까지 검사를 해봐야한다. Deutsch - Jozsa Algorithm의 경우, 시간복잡도 함수는 무려 O(1)이다.
Hadamard Math
이러한 압도적인 효율은 Hadamard Gate의 수학적 특징에서 기인한다.
$H \ket 0 = \frac{\sqrt 2}{2}(\ket 0 + \ket 1)$
$H \ket 1 = \frac{\sqrt 2}{2}(\ket 0 - \ket 1)$
즉, $u \in {0,1}$에 대해 다음과 같이 쓸 수 있다.
$H \ket u = \frac{\sqrt 2}{2} (\ket 0 +(-1)^u \ket 1) = \frac{\sqrt 2}{2} \underset{v \in {0,1}}{\sum} (-1)^{uv} \ket v$
(-1)을 곱해주는 것은 제곱 항인 확률에는 영향을 미치지 않지만 페이즈에는 영향을 미친다. 물리학자들은 이를 일컬어 phase change라고 부른다.
큐빗이 여러개로 확장될 경우는 다음과 같이 일반화 할 수 있다.
$H^{\otimes n} \ket u = H\ket u_1 \otimes H \ket u_2 \otimes … \otimes H \ket u_n= \frac{1}{\sqrt{2^n}} \underset{v \in {0,1}^n}{\sum} (-1)^{u\cdot v} \ket v$
Deutsch - Jozsa Algorithm에서는 $\ket u = \ket{00…001}$인 n+1 짜리 큐빗을 사용한다. 이 경우 $u \cdot v = v_{n+1}$이 되므로 다음과 같이 적을 수 있다.
$H^{\otimes n +1} \ket {00…01} = \frac{1}{\sqrt{2^{n+1}}} \underset{v \in {0,1}^{n+1}}{\sum} (-1)^{v_{n+1}} \ket v $
$= H^{\otimes n} \ket 0 ^{\otimes n} \otimes H \ket 1$
Deutsch - Jozsa Algorithm
$U_f$ 이전 까지는 위에서 설명한 상황을 표현해주는 회로이다. $U_f$는 다음과 같은 함수이다.
$U_f (\ket x ^{\otimes n} \otimes \ket y) = \ket x ^{\otimes n} \otimes \ket {y \oplus f(x)}$
$\ket x^{\otimes n}$과 $\ket y$는 각각 다음과 같다.
$\ket x^{\otimes n} = H^{\otimes n} \ket 0 ^{\otimes n} = \frac{1}{\sqrt {2^n}}\underset{x \in {0,1}^n}{\sum} (-1)^{f(x)} \ket x$
$\ket{y} = H \ket 1 = \frac{1}{\sqrt 2} (\ket 0 - \ket 1)$
이를 $U_f$에 넣으면 다음과 같다.
$U_f (\ket x ^{\otimes n} \otimes \ket y) = ( \frac{1}{\sqrt {2^n}}\underset{x \in {0,1}^n}{\sum}\ket x) \otimes (\frac{\sqrt 2}{2} \ket{f(x)} - \frac{\sqrt 2}{2}\ket{1\oplus f(x)})$
만약 f(x)가 0이면 $(\frac{\sqrt 2}{2} \ket 0 - \frac{\sqrt 2}{2}\ket{1})$
만약 f(x)가 1이면 $(\frac{\sqrt 2}{2} \ket 1- \frac{\sqrt 2}{2}\ket 0)$
이는 다시 다음과 같이 합쳐서 쓸 수 있다.
$(-1)^{f(x)}\frac{\sqrt 2}{2} (\ket 0 -\ket 1)$
이 확률은 얽힘에 의해서 앞부분으로 전이된다. 따라서 다음과 같이 쓸 수 있다.
$U_f (\ket x ^{\otimes n} \otimes \ket y) = ( \frac{1}{\sqrt {2^n}}\underset{x \in {0,1}^n}{\sum} (-1)^{f(x)} \ket x)(\frac{\sqrt 2}{2} \ket 0 -\frac{\sqrt 2}{2} \ket 1)$
뒷 부분은 일종의 상수이다. 앞 부분에는 오라클 f(x)가 $(-1)^{f(x)}$의 형태로 들어가게 되었다. 이를 phase kickback이라고 한다.
여기에 Hadamard Gate를 다시 적용해보자. 위에서 기술한 Hadamard Gate에 대한 공식을 이용하자.
$H^{\otimes n}(\frac{1}{\sqrt {2^n}}\underset{x \in {0,1}^n}{\sum} (-1)^{f(x)} \ket x) = \frac{1}{2^n}\underset{x \in {0,1}^n}{\sum} (-1)^{f(x)} \underset{v \in {0,1}^n}{\sum} (-1)^{x\cdot v}\ket v$
만약 f(x)가 Constant라면 f(x)=c 이므로 밖으로 빼낼 수 있다.
$=\frac{1}{2^n}(-1)^{f(0)} \underset{v \in {0,1}^n}{\sum} [ \underset{x \in {0,1}^n}{\sum} (-1)^{x\cdot v}]\ket v$
이때 $\ket v = \ket {0}^{\otimes n}$일시 $\forall x, x \cdot v = 0 $이므로 $[ \underset{x \in {0,1}^n}{\sum} (-1)^{x\cdot v}] = 2^n$이며
$\ket v \neq \ket 0^{\otimes n}$일시 x의 조합에 대해 $x \cdot v$의 절반은 0이고 절반은 1이므로 $[ \underset{x \in {0,1}^n}{\sum} (-1)^{x\cdot v}] = 0$이다.
따라서 v와 x의 조합에 대해 다음의 결과물이 된다.
$H^{\otimes n}(\frac{1}{\sqrt {2^n}}\underset{x \in {0,1}^n}{\sum} (-1)^{f(x)} \ket x) = (-1)^{f(0)}\ket{0}^{\otimes n}$
이를 측정하면 100%확률로 $\ket 0 ^{\otimes n}$이 된다.
만약 f(x)가 Balanced라면 다음과 같다.
$=\frac{1}{2^n}\underset{v \in {0,1}^n}{\sum} [ \underset{x \in {0,1}^n}{\sum}(-1)^{f(x)} (-1)^{x\cdot v}]\ket v$
이때 $\ket v = \ket 0^{\otimes n}$의 케이스에서는 $(-1)^{x \cdot v} =(-1)^0=1$이 되므로 다음과 같이 쓸 수 있다.
$=\frac{1}{2^n}\underset{v \in {0,1}^n}{\sum} [ \underset{x \in {0,1}^n}{\sum}(-1)^{f(x)} ]\ket v$
그리고 이중 절반은 0이므로 $(-1)^{f(x)} =(-1)^0 =1$이고, 1이므로 $(-1)^{f(x)} =(-1)^1 =-1$이다.
따라서 $[ \underset{x \in {0,1}^n}{\sum} (-1)^{f(x)}] = 0$이므로 $\ket 0 ^{\otimes n}$이 측정될 확률은 0이다.
정리하면 f(x)가 Constant일시 $\ket 0 ^{\otimes n}$가 측정될 확률이 100%이며 f(x)가 Balanced일시 $\ket 0 ^{\otimes n}$가 측정될 확률은 0%이다. 따라서 Deutsch - Jozsa Algorithm을 통해 측정된 큐빗을 관찰함으로써, f(x)가 Balanced인지 Constant인지 알 수 있다.
지금까지 Grover’s Algorithm과 Deutsch’ Algorithm을 살펴보았다. 이 두 알고리즘은 양자 알고리즘의 기본이라고 볼 수 있으며 확률전이와 확률증폭이 어떤 식으로 이뤄지는 지 공부할 수 있는 좋은 사례이다. 어떻게 이뤄지는 지 확실히 숙지해두자.
Sutor, R. (2019). Dancing With Qubits. Birmingham,UK:Packt
Bernhardt, C. (2019). Quantum computing for everyone. Boston, Massachusetts:The MIT Press