Chapter 2. Quantum Gate and Basic Circuit
1. Quantum Gate
Boolean Function이란 19세기 후반 George Boole이 고안해낸 함수로, True 혹은 False 라는 논리값의 모음을 입력값으로 받아서 True 혹은 False를 함수값으로 내보내도록 고안된 함수의 종류이다.
이때 True와 False를 1과 0으로 대체하면 컴퓨터의 Bit에서도 사용할 수 있고 이러한 함수들을 여러개 조합함으로써 복잡한 연산까지 할 수 있다. 이것이 컴퓨터의 가장 기초가 되는 원리이다.
이렇게 컴퓨터의 기본적인 설계에서 사용하는 논리 함수를 Logical Gate라고 한다. 이러한 Gate의 대표적인 예시는 And,Or,Not Gate,Nand Gate 등이 있다
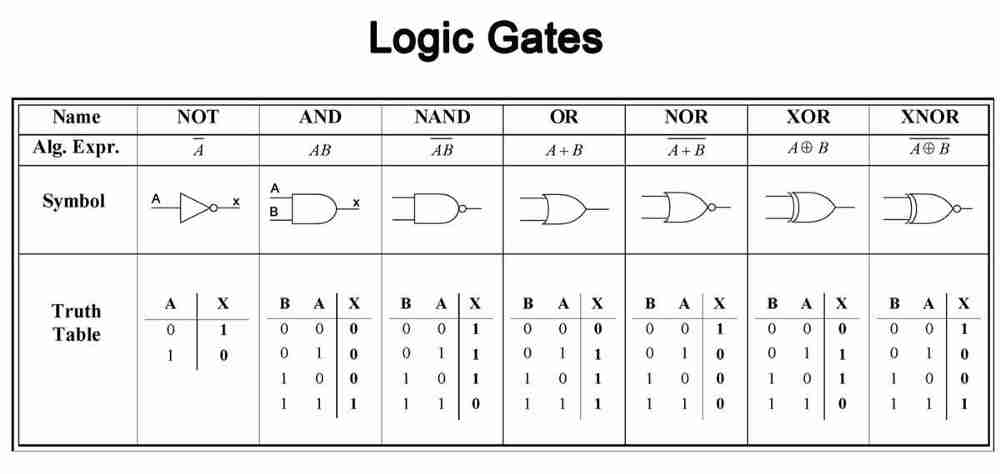
물론 양자컴퓨터에서는 기본 단위로 Bit가 아니라 Qubit를 사용하므로 기존의 Gate와는 다른 Gate를 사용한다.
저번 포스팅에서 이야기 했듯, 양자컴퓨터에서는 하나의 Qubit을 2차원 벡터로 표현하고 선형대수학을 이용해서 계산한다. 따라서 Gate는 n차원 벡터를 인풋으로 받아서 n 차원 벡터를 반환하는 함수이며 그렇기 때문에 벡터와 행렬의 곱셈을 이용해서 표현할 수 있다.
하나의 Input을 받는 Gate로는 Pauli Transformation Gate와 Rotation Gate, Hadamard Gate가 있고 두개의 인풋을 받는 Gate는 CNOT Gate와 SWAP Gate, 세개의 인풋을 받는 Gate로는 Toffoli Gate와 Fredkin Gate 등이 있다. 물론 다른 무수히 많은 Gate들이 있지만 일단은 이 6가지만 알아보자.
1. Single Qubit Gates
Pauli Transformation Gates
Pauli Transformation Gates는 총 4개로 이루어져 있고 하나의 Qubit 만 인풋으로 받으므로 $2 \times 2$ 행렬의 형태이다.
$I = \left[ \begin{array}{cc} \ 1 & 0 \\ 0 & 1 \end{array} \right], X = \left[ \begin{array}{cc} \ 0 & 1 \\ 1 & 0 \end{array} \right] , Y = \left[ \begin{array}{cc} \ 0 & -i \\ i & 0 \end{array} \right] , Z = \left[ \begin{array}{cc} \ 1 & 0 \\ 0 & -1 \end{array} \right]$
어떤 임의의 Qubit $\mid \psi \rangle = \alpha \mid 0 \rangle + \beta \mid 1 \rangle$가 이러한 Gate를 거치면 다음과 같이 변한다.
-
$I\mid \psi \rangle = \alpha \mid 0 \rangle + \beta \mid 1 \rangle$
-
$X \mid \psi \rangle = \beta \mid 0 \rangle + \alpha \mid 1 \rangle$
-
$Y\mid \psi \rangle = -\beta i \mid 0 \rangle +\alpha i \mid 1 \rangle $
-
$Z \mid \psi \rangle = \alpha \mid 0 \rangle -\beta \mid 1 \rangle$
각각의 확률이 어떻게 변하는 지 살펴보자. X Gate의 경우 0과 1의 확률이 뒤바뀌며 Z Gate의 경우 확률은 그대로지만 확률 진폭의 방향은 정반대가 되었다. Y 같은 경우는 Phase가 바뀐 것을 볼 수 있다.
X는 이해가 직관적으로 되지만 Y와 Z는 직관적인 이해가 되지않는다. 다행히, Bloch Sphere를 보면 어떤 변환을 했는지 이해를 할 수 있다.
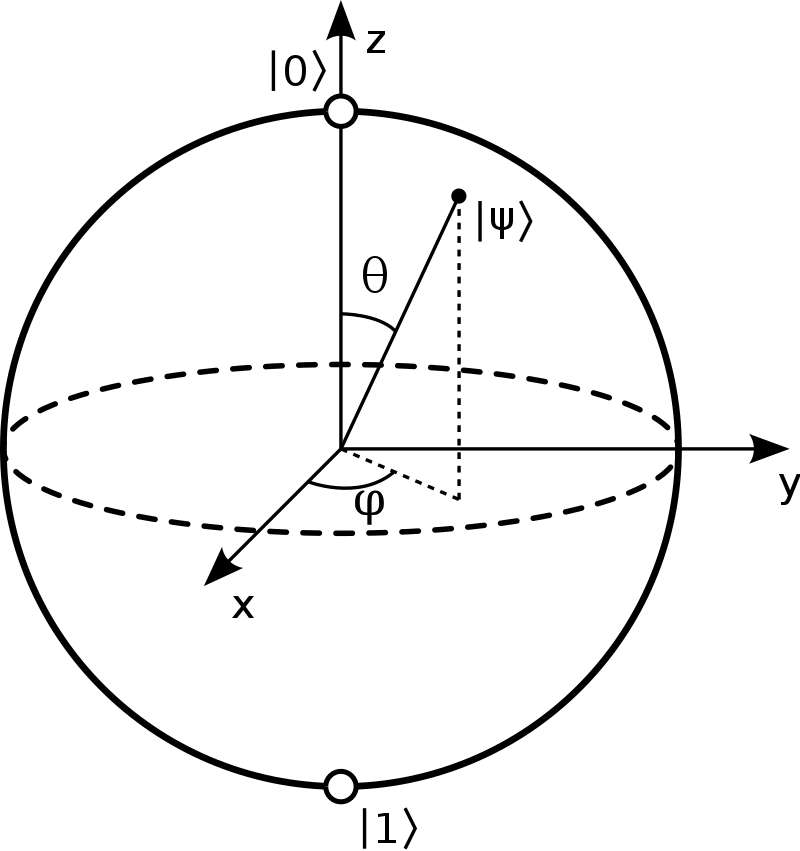
위에서 구한 벡터들과 결과물을 대입해보면 행렬들이 각각 X축, Y축, Z축을 기준으로 180도 회전한 결과물임을 알 수 있다.
Z 축 회전의 경우 수직 방향이 바뀌는 것은 아니므로 확률은 그대로지만 내재되어있는 확률진폭의 방향이 반대가 되는 것을 볼 수 있다.
Y축의 경우 Y=0인 평면에 있는 원형은 $\theta$가 0인, 즉 $e^{i \theta}$가 1인 값들의 집합이고 Phase가 0인 값들이라고 말할 수 있다.
반대로 생각해 $e^{i\theta}$가 1과 0 사이의 값일시, 즉 Phase가 0이 아닐시 y축의 값이 존재 한다는 의미로 이해할 수 있다. 거기에 적절한 i가 곱해짐으로써 y축으로 180도 회전이 된 것이다. 자세한 것은 다른 포스팅에서 다루도록 하겠다.
정리하면 I,X,Y,Z Gate는 Qubit의 상태를 각각의 축에 대해 완전히 반전 시키는 Gate라고 말할 수 있다.
Hadamard Gate
Hadamard Gate는 양자컴퓨터의 핵심이 되는 Gate 중 하나로 다음과 같이 표현된다.
$H = \frac{\sqrt 2}{2}\left[ \begin{array}{cc} \ 1 & 1 \\ 1 & -1 \end{array} \right]$
이 게이트는 완전히 고정된 Qubit인 $\mid 0 \rangle$이나 $\mid 1 \rangle$을 50대 50의 중첩상태로 만들어준다. 즉 아래와 같은 결과물을 갖는다.
-
$H\mid 0 \rangle = \frac{\sqrt 2}{2}\mid 0 \rangle + \frac{\sqrt 2}{2}\mid 1 \rangle = \mid + \rangle$
-
$H \mid 1 \rangle = \frac{\sqrt 2}{2}\mid 0 \rangle - \frac{\sqrt 2}{2} \mid 1 \rangle = \mid - \rangle$
혹은 Y축을 기준으로 90도 꺽어주는 연산이라고 상상할 수 있다.
이외에도 X,Y,Z축을 기준으로 $\psi$도 만큼 회전해주는 Rotation Gate가 있지만 이는 나중에 다시 다루기로 하자.
2. Two and Three Qubit Gates
Qubit 두 개를 한번에 표현할 때는 가능한 모든 경우의 수를 따지는 Tensor Product를 사용한다.
$\mid \Psi_1 \rangle \otimes \mid \Psi_2 \rangle = \left[ \begin{array}{c} \ \psi_{11} \\ \psi_{12} \end{array} \right] \otimes \left[ \begin{array}{c} \ \psi_{21} \\ \psi_{22} \end{array} \right] \\ \qquad \qquad \quad =\left[ \begin{array}{c} \ \psi_{11}\left[ \begin{array}{c} \ \psi_{21} \\ \psi_{22} \end{array} \right] \\ \psi_{12}\left[ \begin{array}{c} \ \psi_{21} \\ \psi_{22} \end{array} \right] \end{array} \right] $
일반적인 선형대수학에서는 Dot Product를 많이 쓰기 때문에 연산자가 생략되어 있으면 Dot Product라고 생각한다. 하지만 양자역학에서는 Tensor Product를 많이 사용하기 때문에 연산자가 생략되어 있다면 Tensor Product라고 보면 된다. 쉽게말해 아래와 같다.
$\mid \Psi_1\rangle \otimes \mid \Psi_2\rangle = \mid \Psi_1 \rangle \mid \Psi_2 \rangle = \mid \Psi_1 \Psi_2\rangle$
이러한 표기하에서 2-Qubit Gates를 살펴보자.
CNOT Gate
CNOT Gate는 Controlled Not Gate의 줄임말로 Quantum Computer에서 Not Gate는 X Gate이므로 CX Gate라고도 불린다.
첫번째 아웃풋은 첫번째 인풋을 그대로 반환하고 두번째 아웃풋은 첫번째 인풋이 1이라면 두번째 인풋에 X Gate를 통과시킨 값을, 0이라면 그대로 통과시킨 값을 반환하는 게이트이다.
행렬로 표기하면 아래와 같다.
$CX = \left[ \begin{array}{cccc} \ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1& 0 \end{array} \right] $
이때, 첫번째 게이트는 두번째 게이트의 작동 유무를 결정하기 때문에 controlled qubit이라고 부른다. CNOT Gate와 유사하게 일부 인풋을 Controlled Qubit으로 설정하는 Gate는 2-Qubit, 3-Qubit에서도 나타난다. CX와 대응되는 CY, CZ Gate도 마찬가지로 생각해볼 수 있다.
CNOT Gate가 특히나 중요한 이유는 나중에 나올 Bell’s Circuit을 구현하는 데 쓰인다는 점에 있다.
나머지는 위의 응용 혹은 쉽게 생각할 수 있는 게이트 들이다.
SWAP Gate
Swap Gate는 말 그대로 두 큐빗의 State를 반전시켜주는 Gate이다. 행렬로 표기하면 다음과 같다.
$SWAP = \left[ \begin{array}{cccc} \ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] $
Toffoli Gate
토폴리 게이트는 CCNOT Gate 혹은 CCX Gate라고도 불리며 세개의 인풋을 받아서 세개의 아웃풋을 보내는 게이트이다.
첫번째와 두번째 큐빗이 모두 1 일때 세번째 큐빗에 NOT Gate를 적용한다.
Fredkin Gate
프레드킨 게이트는 CSWAP Gate라고도 불리며 세개의 인풋을 받아서 세개의 아웃풋을 보내는 게이트이다.
첫번째 큐빗이 1일때 두번째와 세번째 큐빗을 스왑하는 Gate이다.
2. Basic of Quantum Circuit
이제 앞서서 얘기한 Gate들을 조합하면 특수한 역할을 하는 회로를 만들 수 있는데 이를 Quantum Circuit이라고 한다.
IBM에서는 Qiskit이라는 파이썬 모듈을 통해 양자컴퓨터의 회로를 만들고 자기들의 양자컴퓨터에 접속해서 실험할 수 있도록 해주고 있다.
구글이나 마이크로소프트에서도 이러한 양자컴퓨터의 어셈블리 언어를 만들고 있지만 이 부분에서 선구자 역할을 하는 것은 IBM이다. 따라서 Qiskit이 업계의 표준으로써 자리잡고 있다고 볼 수 있다.
이 Qiskit에서는 양자 회로를 다음과 같은 그림으로 표시한다.
왼쪽에서 회로 전체의 인풋이 들어가서 오른쪽으로 흘러가며 Gate를 통과한다. 다른 설정이 없다면 Qubit은 모두 $\mid 0 \rangle$의 상태를 가지며 가장 우측의 계기판 같은 표기는 이를 Measure하라는 것을 의미한다.
Single Qubit Gate의 경우 위에서 적은 영문자들이 그대로 Gate의 상징이 된다. 즉 X가 의미하는 것은 X 게이트이다. 2 - Qubit Gate의 경우 아래와 같은 표기법을 사용한다.
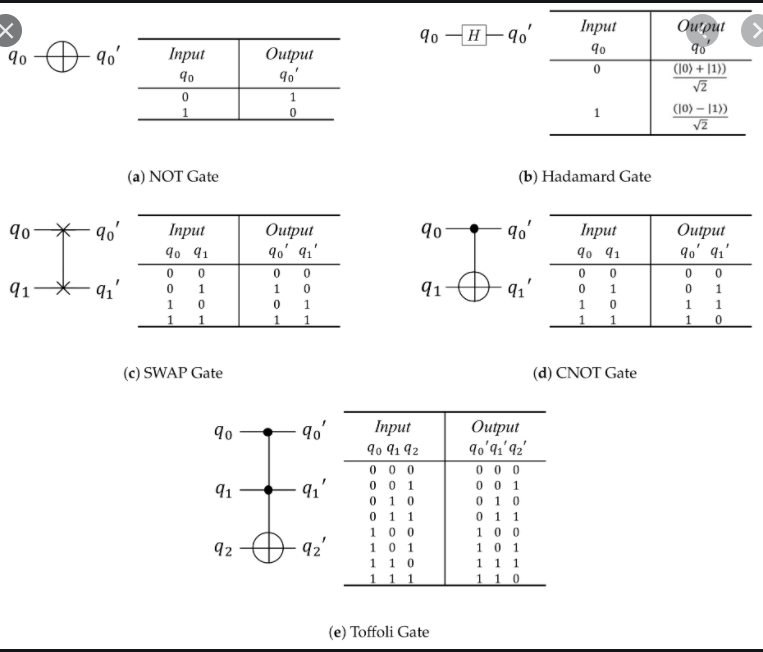
따라서 이를 활용하여 Circuit을 표현할 수 있다.
이제까지는 Quantum Computer의 기초만 다뤘기 때문에 실질적인 역할을 하는것 처럼 보이는 요소는 안했는데, 바로 이 Circuit이 알고리즘의 기본들을 이루며 정말로 어떤 역할을 하게된다.
그러나 내가 관심있는 계산 가속화 부분의 알고리즘인 Shor’s Algorithm이나 Quantum Linear Solver같은 것들은 Phase에 대한 이해가 필수적으로 들어가며 Quantum Fourier Transformation이 다수 사용된다. 따라서 이 부분들은 다음 포스팅에서 복소수와 복소수 공간,Phase와 Fourier Transformation에 대해서 종합적으로 공부를 해본 다음에 다뤄보자.
이번 포스팅에서는 우선 양자 Circuit에서 중요하게 쓰이는 Bell’s Circit과 정보전달 프로토콜인 Superdense Code와 Quantum Teleportation에 대해서 간단하게만 다룰 예정이다.
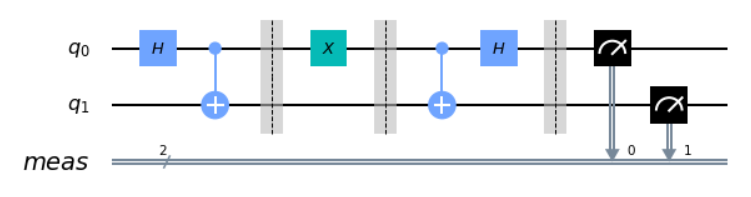
Bell’s Circuit
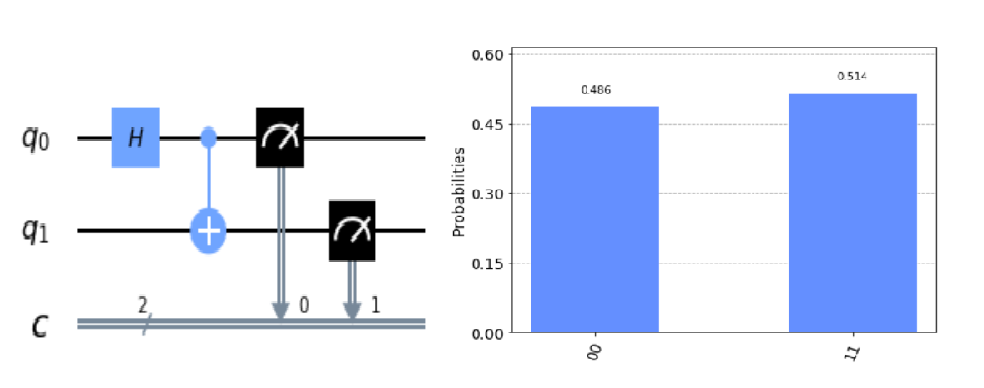
Bell’s Circuit은 위와 같이 Hadamard Gate와 Cnot Gate만 사용되는 단순한 회로이다.
인풋값으로 $\mid 0 0 \rangle $이 들어가니 output으로 50% 확률로 $\mid 00 \rangle$이, 50% 확률로 $\mid 11 \rangle$이 나옴을 확인할 수 있다.
이 결과를 수학적으로 풀어보자.
- Input: $\mid 00 \rangle$
- H 적용 : $(H\mid0 \rangle) \otimes \mid 0 \rangle = \frac{1}{\sqrt{2}}(\mid 0 \rangle + \mid 1 \rangle) \otimes \mid 0 \rangle$
- CNOT 적용: $\frac{1}{\sqrt 2} (\mid 00 \rangle +\mid 11 \rangle)$
00으로 고정된 값을 가지는 Qubit이 Bell’s Circuit을 거친다면 하나가 0이 나오면 나머지도 0이고, 하나가 1이 나오면 나머지도 1인 큐빗이 완전하게 얽혀있는 상태를 얻어낼 수 있다.
이번에는 두번째 Qubit에 X Gate를 적용해서 $\mid 01 \rangle$ Qubit을 Bell’s Circuit에 넣어보자.
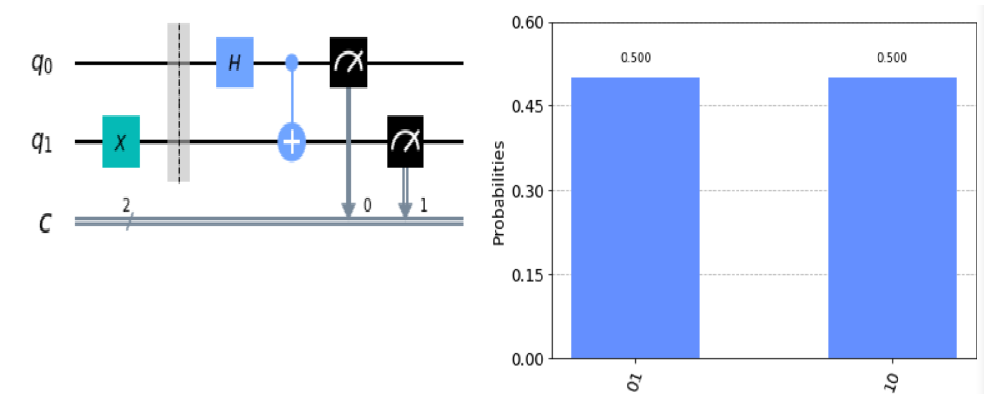
결과물은 대동소이 하지만 이번에는 하나가 0이 나오면 나머지는 1이 나오도록 짜여져있음을 알 수 있다.
즉 Bell’s Circuit은 완전히 얽혀있는 두 큐빗을 만드는데 사용되는 Circuit이다. 특히 이렇게 나올수 있는 4가지 상태를 Bell’s State라고 한다. 이를 이용한 Quantum Computer의 Protocol도 살펴보자.
3. Quantum Protocol
설명은 생략했지만 Qubit는 Circuit을 통해서는 복제가 불가능하다. 물론, 1과 0으로 고정된 Qubit는 bit로 옮겨낸뒤 복제하면 되지만 중첩된 상태에 있는 Qubit은 똑같은 상태를 가지는 Qubit을 만들어낼 수 없다.
이는 COPY($\mid x\rangle, \mid 0 \rangle$)= $\mid x\rangle,\mid x\rangle$이라는 함수가 존재한다고 가정시 모순히 발생하기 때문에 이론적으로도 만들어질수 없음이 증명 되어 있다.
따라서 고전 컴퓨터에서는 정보를 전달할때, 단순히 내가 가지고 있는 비트와 똑같은 비트를 만들어서 전달하면 되지만 양자컴퓨터는 이러한 복제가 불가능하기 때문에 일반적인 정보전달방식을 쓸 수 없다.
그렇기 때문에 양자컴퓨터에서는 특별한 방식의 정보전달방식(프로토콜)을 사용하며 이를 Superdense Code와 Quantum Teleportation이라고 부른다. 이 두 가지 Circuit은 qubit을 bit로, bit를 qubit으로 변환해 줌으로써 정보를 전달할 수 있다.
Superdense Code
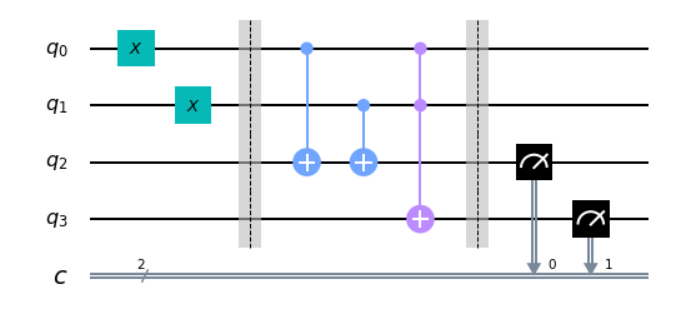
Superdense Code는 하나의 Qubit을 전달함으로써 두개의 Bit를 전달하는 것과 똑같은 효과를 내준다. Superdense Code의 회로는 아래와 같다.
-
점선을 기준으로 첫번째는 전달 이전에 수신자와 발신자가 Bell’s Circuit을 통해 완전히 얽혀있는 두 큐빗을 나눠가지는 상황을 의미한다.
-
두번째는 발신자가 나눠가진 한 Qubit에 대해 전달하고자 하는 Bit에 맞는 Gate를 통과시킨 것이다. 여기서는 X Gate에 통과를 시켰고 0,1의 비트가 전달된다.
-
세번째는 발신자가 자기가 처리한 Qubit을 보내고 수신자가 이제 첫번째에서 가지고 있던 큐빗과 발신자로 부터 받은 큐빗에 Inverse-Bell’s Circuit으로 처리함으로써 bit 정보 2개를 얻을 수 있게 된다.
두 번째에서 과정에서 X 대신 I Gate를 사용할시 00이, X는 01로, Z는 10으로, X에 넣고 다시 Z에 넣으면 11이 최종 결과물로써 반환된다.
따라서 수신자와 발신자가 얽혀있는 두 큐빗을 미리 공유하고 있을때, 발신자는 큐빗 하나를 보냄으로써 비트 두개를 전달한거나 마찬가지인 효과를 낼 수 있다.
Quantum Teleportation
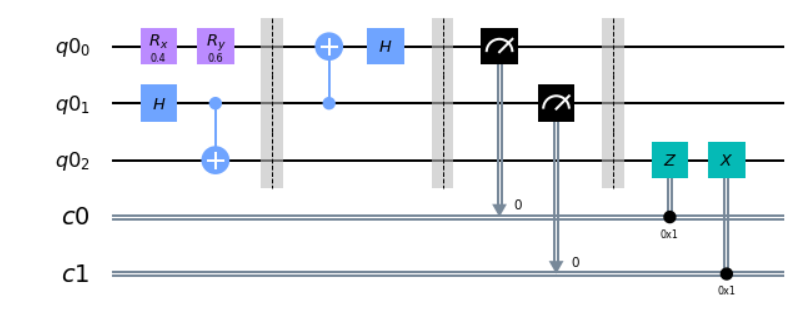
Quantum Teleportation은 역으로 두개의 비트를 보내 한개의 큐빗을 전달하는 방법이다. Quantum Teleportation의 회로는 아래와 같다.
- Superdense Code와 마찬가지로 수신자와 발신자는 Bell’s Circuit에 의해 완전히 얽혀있는 Qubit을 하나씩 나눠가진다. 첫번째 구역의 2,3번째 큐빗이 이를 의미한다. 첫번째 큐빗에서는 발신자가 임의로 상태를 가지는 Qubit을 전달하는 상황을 가정했으므로 아무숫자나 넣어서 Rotate해주는 $R_x$ Gate를 이용해주었다.
- 두번째 구역에서 발신자는 나눠가진 Qubit과 자신이 가지고 있는 임의의 Qubit에 Inverse Bell’s Circuit에 통과시킨다. 그 다음 이 상태들을 측정해서 수신자에게 Bit정보를 보낸다.
- 세번째 구역에서 수신자는 자신이 가지고 있던 Qubit에 대해 발신자로 부터 받은 첫번째 비트가 1일시 Z Gate를, 두번째 비트가 1일시 X Gate를 취해준다. 둘다 1이면 Z와 X 모두 취해준다. 이를 통해 수신자는 발신자가 가지고 있던 Qubit을 전달받을 수 있게 된다.
유의해야할 점은 Qubit은 복제가 안되기에 발신자는 보낸 Qubit에 대한 정보를 잃어버리게 된다. 이를 통해 두가지 비트 정보를 보냄으로써 하나의 Qubit을 전달할 수 있게 된다.
Superdense Code는 납득이 간다 쳐도 Quantum Teleportation은 쉽사리 납득이 가지 않는다. 따라서 실제 수학으로 풀어보자.
첫번째 구역은 문제의 셋팅이므로 두번째 부터 시작하자.
발신자는 자기가 원래 가지고 있던 Qubit이 있다. 이를 $\mid \psi \rangle =\psi_1 \mid 0 \rangle + \psi_2 \mid 1 \rangle$이라고 하자. 이에 대해 두번째 Circuit은 다음과 같은 연산을 한다.
- CNOT Gate
Input : $ (\psi_1 \mid 0 \rangle + \psi_2 \mid 1 \rangle) \otimes (\frac{1}{\sqrt 2} (\mid 0\rangle + \mid 1 \rangle ))$
Output : $\frac{\psi_1}{\sqrt 2} \mid 00\rangle +\frac{\psi_1}{\sqrt 2 }\mid 01 \rangle + \frac{\psi_2}{\sqrt 2 }\mid 11\rangle + \frac{\psi_2}{\sqrt 2} \mid 10 \rangle \\ = \frac{\psi_1}{\sqrt 2}(\mid 00 \rangle + \mid 01 \rangle) + \frac{\psi_2}{\sqrt 2 } (\mid 11 \rangle + \mid 10 \rangle) \\ = \frac{\psi_1}{\sqrt 2}\mid 0 \rangle\otimes (\mid 0 \rangle + \mid 1 \rangle) + \frac{\psi_2}{\sqrt 2 } \mid 1 \rangle \otimes (\mid 1 \rangle + \mid 0 \rangle) $
- H Gate
Input : $\frac{\psi_1}{\sqrt 2}\mid 0 \rangle\otimes (\mid 0 \rangle + \mid 1 \rangle) + \frac{\psi_2}{\sqrt 2 } \mid 1 \rangle \otimes (\mid 1 \rangle + \mid 0 \rangle) $$
Output : $\frac{\psi_1}{\sqrt 2} \frac{1}{\sqrt 2}(\mid 0 \rangle + \mid 1 \rangle) \otimes (\mid 0 \rangle + \mid 1 \rangle) +\frac{\psi_2}{\sqrt 2} \frac{1}{\sqrt 2 } ((\mid 0 \rangle - \mid 1 \rangle)(\mid 0 \rangle + \mid 1 \rangle) \\ =\frac{\psi_1 + \psi_1}{2} \mid 00 \rangle + \frac{\psi_1 + \psi_2}{2}\mid 01 \rangle + \frac{\psi_1-\psi_2}{2}\mid 10\rangle + \frac{\psi_1 - \psi_2}{2}\mid 11 \rangle$
세번째 구역에서는 위의 확률에 따라서 측정을 하게된다. 비트가 00,01,10,11의 확률이 정해지므로 네번째에서 00,01,10,11이냐에 따라 각각 I$\mid b_{00} \rangle$,X$\mid b_{00} \rangle$,Z$\mid b_{00} \rangle$,XZ$\mid b_{00} \rangle$ 네 가지 케이스의 게이트를 연산하는 것 역시 확률적으로 이뤄진다.
결과적으로 네번째 구역을 통해 수신자는 발신자가 가지고 있던 Qubit과 똑같은 Qubit을 얻게된다.
이렇게 기본적인 Quantum Computing의 요소에 대해서 알아봤다. 그러나 양자컴퓨터를 이용한 가속화 알고리즘들을 알려면 Phase와 Fourier Transformation에 대한 이해가 필수적이다. 따라서 다음 포스팅에서는 이 부분만 집중적으로 다룰 예정이다.
Sutor, R. (2019). Dancing With Qubits. Birmingham,UK:Packt
Bernhardt, C. (2019). Quantum computing for everyone. Boston, Massachusetts:The MIT Press