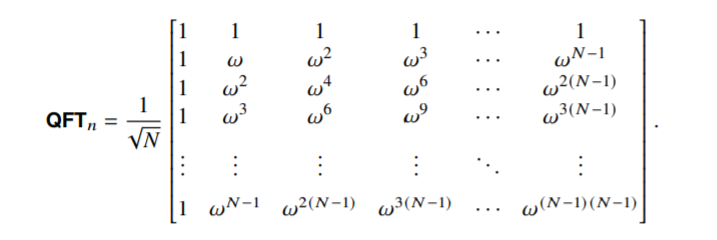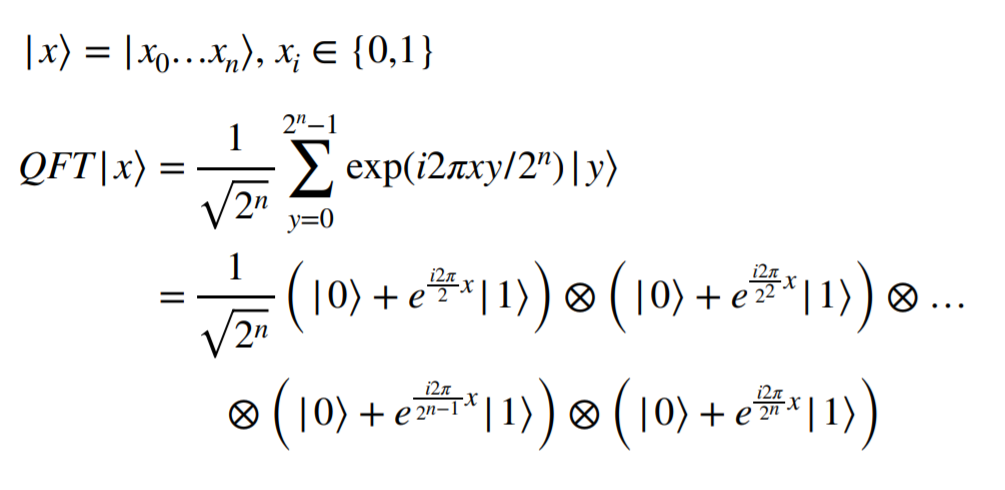Chapter 3. Complex Number and Quantum Fourier Transformation
양자 컴퓨터의 소프트웨어를 구현하기 위해서는 복소수에 대한 이해가 필수적이다. 그러나 통계학에서는 복소수를 그다지 다루지 않기 때문에, 나의 지식은 고등학교 수준에서 멈춰있다.
따라서 더 깊은 양자 컴퓨터를 다루기 위해서 우선 복소수에 대해서 공부를 하고 넘어가자. 이 포스팅의 내용은 “Dancing with Qubits”, Robert S. Sutor를 참고하였다.
1. 복소수의 기본
복소수의 정의
복소수는 실수의 확장판으로 다음과 같이 정의된다.
$C := {z \mid z= a+bi,a,b\in R,i^2=-1}$
여기서 i는 한글로는 허수라고 불리며 영어로는 imaginary number라고 부른다.
이때, a를 실수부(real part)라고 부르며 Re(z)라고 표현하며 b를 허수부(imaginary part)라고 부르며 Im(z)라고 표현한다. 따라서 모든 실수는 허수부가 0인 복소수라고 말할 수 있다.
실수에서는 두 원소간의 order를 정의할 수 있지만 허수에서는 불가능 하다. 따라서 실수는 Ordered Field인 반면 복소수는 Not ordered Field이다.
또한 $z_1=z_2$ iff $Im(z_1)=Im(z_2)$ and $Re(z_1)=Re(z_2)$ 이다. 즉 실수부와 허수부는 섞일 수 없는 단절된 공간이라고 생각할 수 있다.
복소수의 기본 연산
- $0 = 0+0i$
- $1 = 1+0i$
- $-(a+bi)=-a-bi$
- $(a+bi)+(c+di)=(a+c)+(b+d)i$
- $(a+bi) \times (c+di) = (ac-bd)+(ad+bc)i$
- $Re((a+bi)\times(c+di))=ac-bd$
- $Im((a+bi)\times(c+di))=ad+bc$
켤레복소수
켤레복소수는 영어로는 Conjugate Complex Number라고 부르며 복소수 $z=a+bi$에 대해 conjugate of z는 $\bar{z}$라고 쓰며 a-bi로 계산된다.
켤레복소수에는 다음과 같은 성질이 있다.
- $z \bar{z} = a^2+b^2$ ; The product of complex number and its conjugate is non-negative real number
- $z=0$ iff $\bar{z} =0$
- $Re(z)=Re(\bar z) = a$
- $Im(z)=-Im(z)=b$
- If $Im(z)=0$, then $z=\bar{z}$
켤레 복소수는 복소수의 역수를 계산하는데 중요하게 쓰인다.
$z^{-1}=\frac{1}{z}=\frac{\bar z}{\bar z z} = \frac{a-bi}{a^2+b^2} \\ \quad =\frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i$
켤레복소수의 사칙연산은 아래와 같이 정의된다.
- $z = \bar{\bar{z}}$
- $\overline{z^{-1}}=\frac{1}{\bar{z}}$
- $\overline{z+w} = \overline{z}+\overline{w}$
- $\overline{z-w}=\overline{z}-\overline{w}$
- $\overline{z\times w} = \overline{z} \times \overline{w}$
복소수의 측정
복소수의 절대값은 켤레복소수를 이용하여 다음과 같이 정의된다.
$\mid z \mid = \sqrt{z\overline{z}}$
따라서 이를 이용하여 실수에서 쓰는 p-norm을 적용할 수 있다.
$\parallel z \parallel_p = (\sum_{i=1}^n \mid z_i\mid^p)^{1/p} $
Complex Dot Product는 다음과 같이 정의된다.
$\left< z_1,z_2\right>=\sum_{i=1}^n z_{1i}\times \overline{z_{2i}}$
행렬곱을 이용해서 표현할때는 다음과 같이 표기할 수 있다.
$\left< z_1, z_2\right> = z_2^hz_1$ (h means conjugate transpose)
따라서 L2-norm은 아래와 같이 표기할 수 있다.
$\sqrt{z_2^hz_1}$
또한 Norm을 이용하여 Metric까지 확장시킬 수 있다.
$(\parallel z_1-z_2\parallel_p)^{1/p}$
위와 같은 Dot-product를 Inner product로 정의함으로써 자연스럽게 Norm과 Metric을 정의할 수 있게 되고, 이들은 모두 각자의 공리를 만족한다.
또한, $C^n$을 Complete Inner Product Space인 Hillbert Space로 볼 수 있고, Hillbert Space의 성질들을 이용할 수 있다.
2. 복소수의 이해
복소 평면과 Polar Form
복소수의 정의 z=x+yi (x,y는 실수)를 이용하여 2차원 좌표평면 안에서 복소수를 표현할 수 있다.
기존의 2차원 실수 좌표평면에서 (0,1) basis를 (0,i) basis로 바꾼 것이다. 이를 통해 C의 모든 원소를 표현할 수 있다. 그런데 잘 보면 z가 (x,y) 위의 점이므로 각도를 이용해 $(r \cos \theta , r \sin \theta)$로 표현할 수 있음을 알 수 있으며 따라서 $z= x+yi = r\cos \theta +ri \sin \theta$이다.
r을 묶어내면 $\sin \theta + i \cos \theta$이므로 오일러의 공식을 이용해 모든 복소수는 다음과 같이 표현 할 수 있다.
$z= x+yi = r e^{i\theta}$
기존의 $z=x+yi$ Form을 Cartesian Form이라고 하며, $z= re^{i\theta}$ Form을 Polar Form이라고 한다.
위의 그림을 보면 $z$의 conjugate는 $\theta$가 역으로 돌아간 것이므로 다음과 같이 표현할 수 있다.
$\overline{z} = x-yi = re^{-i\theta}$
따라서 이의 절대값을 구해보면 다음과 같다.
$\mid z \mid = \sqrt{z\times \overline{z}} = \sqrt{r^2e^{i \theta-i\theta}}=r$
카르테잔 폼에서 z는 실수부 x와 허수부 y의 2차원의 복잡도를 가진 수 였는데, 폴라 폼에서는 복소수의 크기(Norm)을 표현하는 r과 실수부와 비례한 복소수의 비중을 나타내는 $\theta$의 2차원의 복잡도를 가진 수로 바꿔서 볼 수 있다.
Bloch Sphere
위에서 봤던 기본적인 복소수의 정의를 통해 복소수 한개가 실수차원+ 복소수차원의 2차원 공간을 가짐을 확인했다.
Quantum Computer에서 사용하는 양자는 현실의 3차원에서 구성되어 있으므로 이를 표현을 하기 위해서는 3차원 공간이 필요하다. 양자컴퓨터에서는 허수를 도입한 Bloch Sphere를 사용함으로써 이를 표현한다.
Qubit의 State를 표현하는 notation을 다시보자.
$\mid \psi \rangle = a \mid 0 \rangle + b\mid 1 \rangle ,\quad a,b \in C$
따라서 아래와 같이 표현할 수 있다.
$\mid \psi \rangle = r_0e^{i\phi_0}\mid 0 \rangle + r_1e^{i\phi_1} \mid 1\rangle \\ \quad = e^{i\phi_0}(r_0 \mid 0 \rangle + r_1 e^{i\phi_1-i\phi_0}\mid 1 \rangle )$
양자컴퓨터에서는 0과 1의 계수인 확률진폭이 중요한데 $e^{i\phi_0}$는 이에 대해 영향을 미치지 않으므로 버릴 수 있다.
$\ \quad \approx r_0 \mid 0 \rangle + r_1e^{i\phi}\mid 1 \rangle$
여기서 $\parallel \mid \psi \rangle\parallel_2 =$ 1이므로 하나 더 제약을 걸 수 있다.
$\langle \psi \mid \mid \overline \psi\rangle = r_0^2+r_1^2e^{i\phi-i\phi} \\ \qquad \quad = r_0^2+r_1^2=1$
즉 $r_0,r_1$은 다시 $\cos \theta , \sin \theta$로 표시할 수 있으므로 다음과 같이 적을 수 있다.
$\qquad \ \quad = \cos \frac{\theta}{2} \mid 0 \rangle + \sin \frac{\theta}{2} e^{i\phi} \mid 1 \rangle$
따라서 하나의 Qubit은 $\theta,\phi$에 의존하는 2차원 subspace이며 $\phi_0$는 무시되었으므로 4차원에서 하나를 줄인 3차원에서 다음과 같이 표현 될 수 있다.
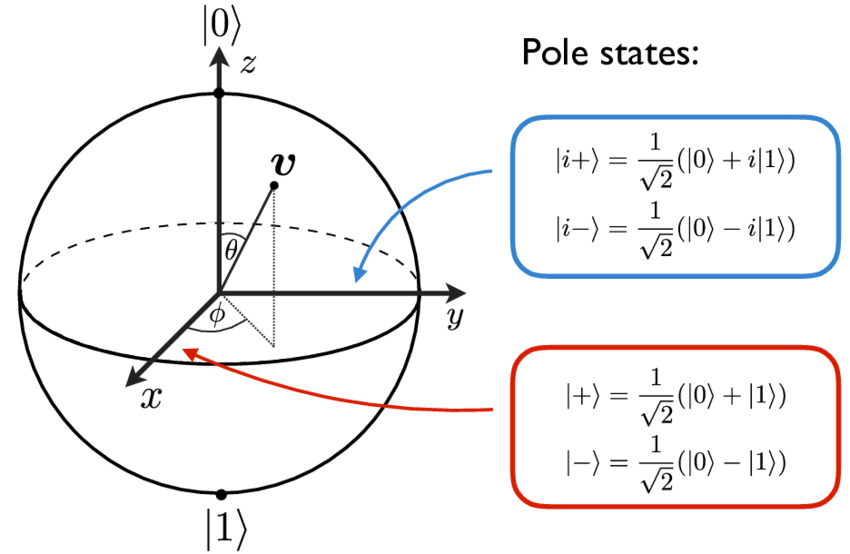
이를 Bloch Sphere라고 한다.
특별히 $e^{i\phi}$부분을 Quantum Phase라고 부른다. Phase는 위상이라고 불리며 물리학에서 여러가지 의미를 가지는 용어인데, 적어도 여기서는 $e^{i\phi}$로 한정짓자. 수많은 양자컴퓨팅 알고리즘이 이 Phase에 대한 추정을 한 후 시작된다.
3. Quantum Fourier Transformation
Fourier Transform
Fourier Transform은 시간에 관한 파동함수를 빈도에 대한 분석의 꼴로 바꿔주는 변형이며 아래와 같은 수식을 가진다.
$\hat{f}(x) = \int_{-\infty}^{\infty} f(t)e^{-2\pi itx} dt$
일반적인 버전에 대해서는 링크에서 매우 직관적으로 설명하고 있으니 참고하면 되겠다.
일단 대략적으로 공부를 해보니 모든 불규칙적인 Signal은 무수히 많은 Sin함수와 Cos함수의 합으로 표현할 수 있는데, Foulier Transform을 이용해서 이 Sin,Cos함수의 진폭과 주기에 대해서 분석할 수 있다는 것이다.
$f(t) = \sum_{i=0}^{N} \eta_i (\cos(2\pi tk_i)+i\sin(2\pi tk_i))$ 여기서 $\eta_i$는 진폭, $k_i$는 주기이다.
이에 대한 fourier transform을 할시
$\hat{f}(x)$가 높게 치솟는 부분의 입력값이 주기이며 치솟는 만큼이 진폭을 표현한다.
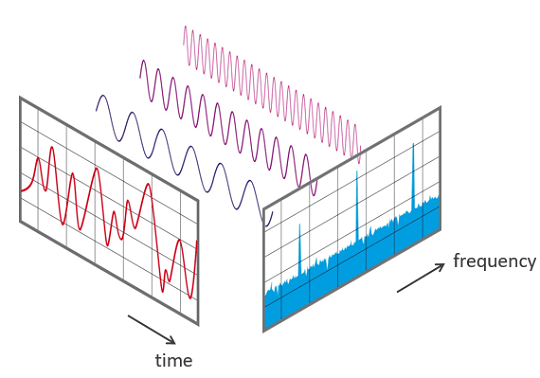
복소수를 사용한 이유는 복소평면에서 주기함수를 더 아름답게 표현하기 위함이라고 한다. 이를 분석함으로써, Signal의 원래 구성을 분석할 수 있다고 한다.
Quantum Fourier Transfrom
물리학에서는 관측되기 전의 양자 상태는 파동이며 그렇기에 파동함수의 형태로 나타낼 수 있다고 한다. 앞에서 정의했던 양자상태를 Dirac Notation으로 표기했던 것은 이것을 위함이었다.
따라서 Quantum Computer에서 Fourier Transform을 하겠다는 것은 양자상태를 분석 하겠다는 것으로 이해할 수 있겠다.
하지만 파동함수는 커녕 관련 내용에 대해서 지식이 전무하고, 또 실제 양자컴퓨터에서 Fourier Transform을 할때는 조금 다른 목적으로 사용하는 것 처럼 보인다. 따라서 수학적인 Notation만 따라가도 충분할 것 같다.
n개의 qubit을 가지는 모든 Qubits는 다음과 같이 표현가능하다.
$\mid \psi \rangle = \underset{j=0}{\overset{2^n-1}{\sum}} a_j \mid j \rangle_n = \underset{j=0}{\overset{N}{\sum}} a_j \mid j \rangle_n$
여기서 $a_j$는 확률진폭이며 $\mid j \rangle_n$는 베이시스이다. n개의 큐빗이 가능한 상태는 $2^n$개이며 $\mid j \rangle_n \in R^{2^n}$이다.
이에 대한 Quantum Fourier Transform of n qubit(aka.$QFT_n$)은 다음과 같이 정의된다.
$QFT_n : \mid \psi \rangle = \underset{j=0}{\overset{N-1}{\sum}} a_j \mid j \rangle _n \rightarrow \underset{j=0}{\overset{N-1}{\sum}} b_j \mid j \rangle_n$
where $b_j = \frac{1}{\sqrt{N}}\underset{k=0}{\overset{N-1}{\sum}} a_k e^{\frac{2\pi jki}{N}} = \frac{1}{\sqrt{N}}\underset{k=0}{\overset{N-1}{\sum}} a_k \omega^{jk} \quad \mbox{where }\omega = e^{\frac{2\pi i}{N}}$
이러한 연산은 인풋의 선형 변환으로만 이루어져 있으므로 행렬을 통해서 표현할 수 있다.
1개의 Qubit에 대한 QFT는 Hadamard Gate와 같다.
n개의 Qubit에 대한 QFT 변환의 결과는 아래와 같다.
이를 잘 살펴보면 $\mid 0 \rangle, \mid 1\rangle$의 확률은 같게 유지되면서 Phase만 변화한다. 구체적으로 n번째 qubit의 phase가 $2\pi i \frac{x}{2^{n}}$만큼 이므로 $\phi = \frac{x}{2^n}$만큼 회전한다고 볼 수 있다. Bloch Sphere에서 보면 z=0을 유지하면서 z방향으로 $\frac{1}{2^n}$만큼 로테이팅한다고 해석할 수 있다.
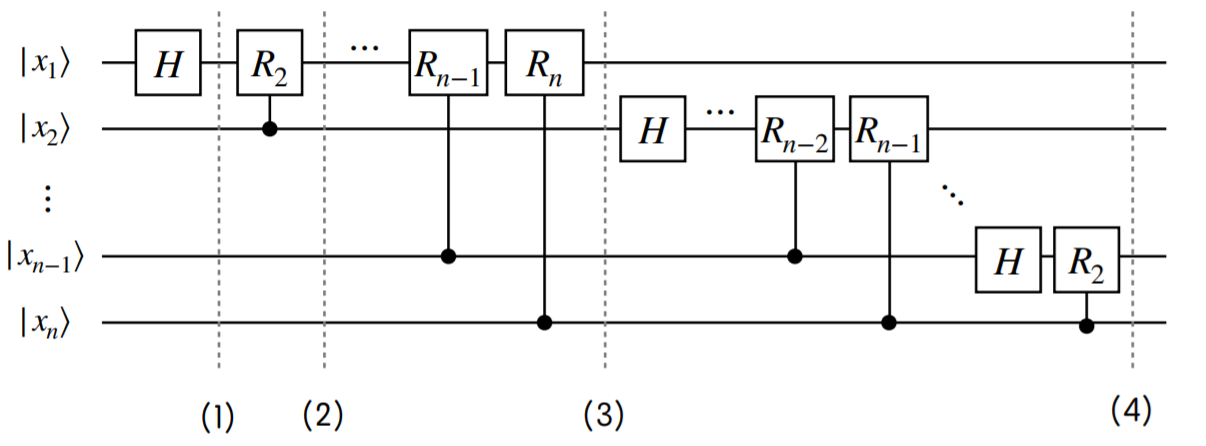
Circuit으로는 아래와 같이 표현할 수 있다. 이때, $CR_k$ gate는 Controlled $Z^{1/k}$ Gate이다. Z Gate가 Z방향으로 180도 회전이므로 $Z^{1/k}$ Gate는 Z방향으로 $180/2^k$도 회전이다.
즉 QFT를 통해서 0 혹은 1 방향 Qubit을 50:50의 확률로 만들고 phase를 $2^n$만큼 쪼갠 것을 표현할 수 있다.
이러한 Quantum Fourier Transform은 양자컴퓨터의 여러가지 알고리즘에 적용해서 사용할 수 있다. 다음 포스팅에서는 이러한 Phase를 이용한 여러가지 알고리즘들에 대해서 알아보도록 하겠다.
Sutor, R. (2019). Dancing With Qubits. Birmingham,UK:Packt
Bernhardt, C. (2019). Quantum computing for everyone. Boston, Massachusetts:The MIT Press