H.G Min

H.G Min

Yonsei University,Korea Mar.14-present
- M.A. expected in applied statitstics
- B.A. in applied statistics

0. Generative Model

우리가 통계학의 기본에서 배우는 대부분의 모델들은 Discriminant Model이다. 통계학적으로 표현하자면 $Pr(Y \mid X)$이며 이것이 가정하는 상황은 X 데이터를 알때 Y 데이터의 확률을 구하는 것이라고 말할 수 있다.

그러나 이와는 다르게 Generative Model이라는 개념을 이야기 할 수 있다. 이를 통계학적으로 표현하자면 $Pr(Y,X)$이며 X와 Y 간의 정보에 대한 위계가 없는 상황을 가정하는 것이라고 말할 수 있다. 이는 인풋 데이터에도 자연 확률적인 요소를 넣은 개념이라고 볼 수 있고, Data Generating Process 그 자체를 추정하고자 하는 개념이라고 생각할 수 있다.
더욱이 Discriminant Model을 $Pr(Y\mid X) = \frac{Pr(Y,X)}{Pr(X)}$로 표현할 수 있으므로 좀 더 일반적인 모델이라고 말할 수 있다.

수학적으로는 둘의 차이를 명확하게 알 수 있지만, 실용적으로 어떤 차이가 있는지는 생각하기 힘들다. 좀 더 생각해보자. 만약 이 Generative Model을 추정해낸면 인풋 X를 알때 그와 동등한 위계를 가지는 X’를 확률적으로 만들어 낼 수 있다.
이를 통해 결측치를 채워 넣을 수도 있지만 그보다 좀 더 팬시한 사용처로 인공적으로 사진이나 문구 등을 만들어 낼 수도 있다. Generative Model을 이용해 X’을 생성해내는 방식은 다음과 같다.

  1. 주어진 데이터 X에 대해 잠재변수 $\theta$의 분포 $Pr(\theta \mid X)$ 를 임의로 추정한다 .
  2. $Pr(\theta \mid X)$ 를 이용해 $Pr(X,\theta)$를 추정해낸다.
  3. 이를 이용해 새로운 데이터 생성 모델 $Pr(X’ \mid \theta)$를 역산해낸다.
  4. 역산해낸 분포를 이용해 새로운 X를 발생시킨다.

이러한 발생모델을 찾아내는 기법으로 유명한 것에는 AutoEncoder와 GAN이 있다. 이번 포스팅 시리즈에서는 다음과 같은 이야기들을 해보려고 한다.

A. Generative Model과 AutoEncoder의 General Preview

B. Regularized Autoencoder

C. Variational Autoencoder

D. Generative Adversary Network

E. Normalizing Flow

1. Regulized AutoEncoder

Regulized AutoEncoder란 말그대로 제약을 걸어준 오토인코더이다. 일반적으로 제약이 없다면 오토인코더는 인풋과 완전히 똑같은 아웃풋을 만들어낸다. 여기서 제약은 Latent Space의 차원개수도 포함한 이야기이며 즉 다음과 같은 구조를 띈다.

그런데 이러한 상황은 그다지 의미가 없을 때가 많다. 오토인코더의 목적은 1. 적은 정보를 이용하여 원본 데이터를 담거나 2. 원본 데이터와 유사한 맥락을 가지지만 완전히 똑같지는 않은 데이터를 만들어내거나 3. 원본 데이터를 요약할 수 있는 핵심적인 정보(Factor)를 추출하는 것에 있는데, 제약없이 구성해버리면 이런 목적을 만족할 수 없기 때문이다.

따라서 오토인코더에는 적절한 제약을 줌으로써 위의 세 가지 목적을 만족시킨다. 영문 위키피디아에서는 이러한 Regularized AutoEncoder로 몇가지를 예시로 들고 있다. 각각 알아보자.

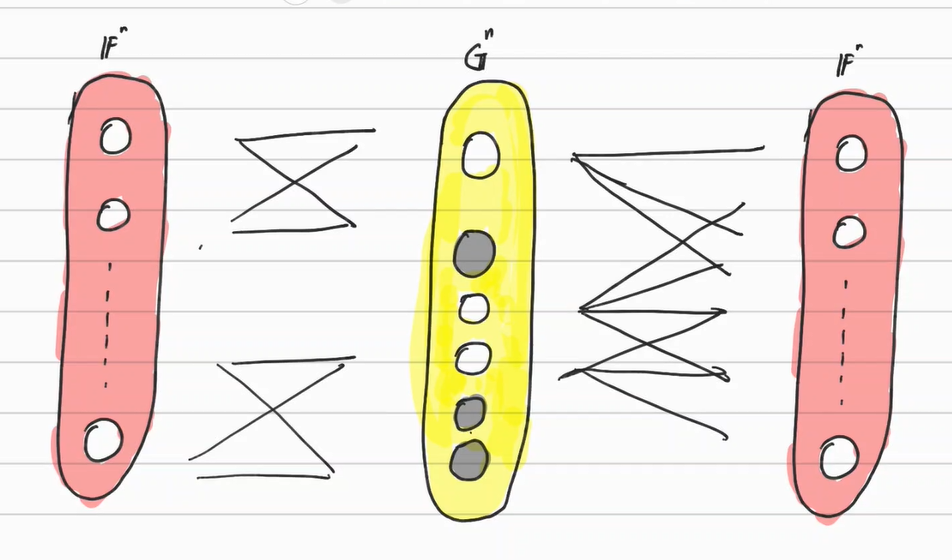
2. Sparse AutoEncoder

Sparse는 뜸한, 희박한을 의미한다. 데이터 사이언스에서 자주 사용하는 용어로 데이터가 Sparse하다는 것은 결측치가 많거나 관측치가 적다는 것을 의미한다. 따라서 데이터가 Spase하다는 것은 그다지 좋은 신호가 아니다. 그러나 요인분석이나 차원축소의 결과가 Sparse하다는 것은 고려해야하는 요인의 개수가 압축 되어있음을 의미하므로, 오히려 목표로 하는 결과라고 말할 수 있다.

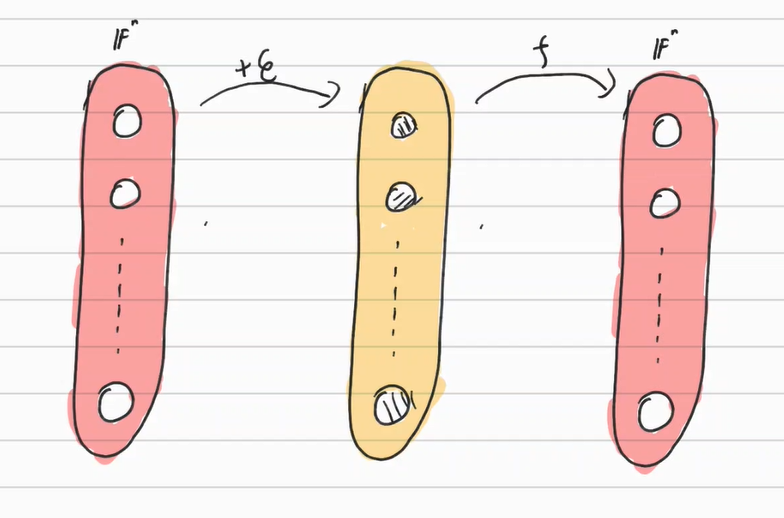
Sparse AutoEncoder는 이와 유사하게 Latent Space를 Sparse하게 만듬으로써 공간을 압축시킨다. 아래의 그림을 참고하자.

이러한 구조를 만들기 위해서는 그저 목적함수에 Sparsity Penalty을 추가해줘서 Latent Space의 Non-Zero 차원의 개수에 페널티를 주면 된다. 이를 통해 Latent Space의 한 원소가 0 혹은 그에 가까운 수를 반환하게끔 만든다. 즉 다음과 같다.

$\underset{f,g}{\min} E(f,g) = L((g\circ f)(x),x) + \Omega (f(x))$

위는 가장 범용적인 형태라고 말할 수 있으며 일반적으로는 다음과 같은 형태의 제약을 둬서 문제를 단순하게 만든다.

  • 함수 f,g - Autoencoder는 Neural Net으로 구성하는 것이 거의 표준으로 자리잡아있다. 따라서 f와 g를 Neural-Net이라고 생각해주면 함수를 대상으로 최적화를 해주는 것이 아니라 Neural Net 내부의 파라미터를 최적화 해주는 문제가 된다. 물론 히든레이어까지 추가해줘도 된다.

  • Loss Function - 손실함수는 다양하게 둘 수 있지만 사실은 Back-Propagation을 용이하게 만들기 위해 대부분 L2-Penalty로 둔다. 데이터 프레임이나 이미지를 대상으로 할 경우 Trace Norm, Operator Norm, Frobenius Norm등을 고려할 수도 있겠다.
  • Sparsity Penalty - Sparsity Penalty로 대표적으로 많이 사용하는 것이 Kull-Back Leibler Divergence와 L1 Penalty이다. 이에 대해서 좀 더 살펴보자.

L1- Penalty

사실 Sparsity Penalty에 가장 적합한 것은 L0-Norm일 것이다. 여러번 포스팅에서 다뤘지만 L0-Norm은 $\mathbb{R}^n$에서 0이 아닌 원소의 개수이며 Sparsity의 정의를 거의 직접적으로 표현한 개념이다. 그러나 이 L0-Norm은 사실 Norm의 공리를 만족하지 못해 Norm도 아니고 미분도 불가능하다. 따라서 L0-Norm을 직접적으로 사용해서 최적화를 하는 것은 거의 불가능하다.

따라서 이를 대신해서 사용해주는 것이 L1-Penalty이다. L1 - Penalty의 모양의 특징이 그나마 L0 - Penalty와 유사하기도 하고 L1-Penalty는 다른 Penalty와는 다르게 0을 취할 수 있기 때문이다. 즉 다음과 같다.

$\Omega (x) = \lambda \sum \mid f(x_i) \mid$

Computer Science에서는 무조건 정확히 근사할 수 있는 모형보다는 속도와 적절한 절충점을 가진 모형을 선호한다. CS에서 L1-Norm은 Soft-Thresholding의 형태로 매우 쉽게 다루고 있는 유형 중 하나이기 때문에 다른 것보다 더 사용된다고 말할 수 있다. (https://hgmin1159.github.io/convex/firstorder3/의 ISTA 예시 참고)

Kullback - Leibler Divergence

Kullback-Leibler Divergence는 Entropy에 대한 Bregman Divergence이며 다음과 같이 정의된다.

$KL(p \mid \mid q) = \int p(x) \log \frac{p(x)}{q(x)}dx$

이는 함수를 인풋으로 받는 Functional이며 함수와 함수간의 거리를 측정해주는 함수이다. 좀 더 유용한 해석으로 p 함수 대신 q 함수를 사용했을때의 정보 손실량이라고 해석할 수 있다. $p(x),q(x)$는 통계학에서는 주로 확률밀도함수가 되며 따라서 근사함수의 적절성을 판단하는 지표가 될 수 있다. (https://hgmin1159.github.io/dimension/mf1/ 참고)

형태를 잘 살펴보면 $E_p(\log p(x)-\log q(x))$이며 p와 q가 같은 형태에 다른 모수를 가진 다고 가정하면 결국 Score Function의 기댓값 차이라고 생각할 수 있다. 거기에 더해 p(x)가 참인 상황을 가정하는 것이므로 $\log p(x)$는 $\log q(x)$보다 항상 크다. 따라서 $KL(p \mid \mid q)$은 항상 Non-Negative이다. 그러나 형태에서 볼 수 있다시피 Symmetirc 하지는 않기 때문에 Metric의 공리는 만족하지않아서 Metric은 아니다.

AutoEncoder는 대부분 Neural Network를 이용해서 구현하는데 이때 Latent Factor Layer에 도달하는 링크함수를 시그모이드 함수로 둬서 0~1사이의 수로 만든다. 이때 i번째 데이터가 오토인코더에 들어갔을 때 Latent Space의 j번째 원소에 반환되는 값을 $h_j(x_i)$라고 했을때 모든 데이터에서 나오는 j번째 원소 평균값은 $\hat{p}_j = \frac{1}{m} \sum [f_j(x_i)]$이라고 말할 수 있다. 이 $\hat p_j$을 모수로 가지는 베르누이 분포와 사전에 정해둔 Sparcity Parameter $p_j$를 모수로 가지는 베르누이 분포와의 Kullback Leibler Divergence를 Sparcity Penalty로 삼을 수 있다. 즉 다음과 같다.

$\Omega (x) = \sum_{j=1}^n KL(f_j(x ; p_j) \mid \mid f_j(x ; \hat p_j)) \\ \qquad = \sum_{j=1}^n [p_j \log \frac{p_j}{\hat p_j} + (1-p_j) \log \frac{1-p_j}{1-\hat p_j}]$

여러가지 문헌을 찾아봤지만 굳이 까다롭게 Kullback Leibler Divergence를 사용하는 이유에 대해서는 명확하게 알기 어려웠다. 이런 방식을 취한 이유에 대해서 생각해보았다. 시그모이드 함수는 대부분의 함수값을 1 혹은 0에 가깝게 만든다. 따라서 이를 파격적으로 해석하자면 $h_j(x) \in {0,1}$(비활성/활성)이라고 볼 수 있고 따라서 $\hat p_i$은 어느 한 원소가 Non-Zero일 확률에 대한 추정값이라고 해석할 수 있다.

따라서 Kullback Leibler Divergence는 베르누이 분포의 영역에 넣어서 확률분포간의 거리를 페널티를 삼음으로써 전체의 $p_i$만큼을 Non-Zero가 되게끔 유도하는 방식이라고 말할 수 있다.

그 외에 제안되는 방식은 Latent Factor의 절대값들을 정렬한 뒤 처음 K-개만 사용함으로써 Sparcity를 이야기하는 K-Sparse AutoEcoder와 특정 Thresold 아래의 값들을 모두 0으로 만드는 Activation Function인 ReLu 함수를 능동적으로 활용하는 방식들이 있다.

3. Denoising Autoecoder

Denoising AutoEncoder는 인풋에 섞여있는 노이즈를 깨끗하게 만드는 것을 목적으로 삼은 AutoEncoder 기법이다. 인풋 데이터 $x$를 임의로 노이즈가 낀 데이터로 변환 시킨 뒤($\tilde x $) 이를 원본 데이터로 복구시키기 위한 함수를 구성한 뒤($f( \tilde x)$) 원본과의 차이를 목적함수로 둠으로써 구조를 완성한다. 즉 다음과 같다.

$\underset{f}{\min} L(f(\tilde x), x)$

이런 단순한 구조로 학습시킨 모델도 괜찮은 효율을 보인다는 것이 알려져 있다. 아래는 Denoising AutoEncoder로 학습시킨 모델의 각각 레이어 아웃풋들이다.

일반적인 Autoencoder와 다른 점은 물론 Denoing 과정이다. 유용하게 쓰는 Denoising 함수 $\tilde x = d(x)$로는 다음과 같은 것들이 있다.

  • Additive White Gaussian Noise(AWGN) - 단순히 기존 데이터에 $\epsilon_i \overset{iid}{\sim} N(0,\sigma^2)$를 추가하는 기법

  • Masking noise - 랜덤으로 추출된 데이터 변수들을 모두 0으로 만듬으로써 노이즈를 형성하는 기법

  • Salt-and-pepper noise - 랜덤으로 추출된 변수들을 확률적으로 Maximum 혹은 Minimum으로 만듬으로써 노이즈를 형성하는 기법

참고자료

위키피디아 - https://en.wikipedia.org/wiki/Autoencoder#Variations

medium - https://medium.com/@syoya/what-happens-in-sparse-autencoder-b9a5a69da5c6

Stanford Open Lecture Nore - https://web.stanford.edu/class/cs294a/sparseAutoencoder.pdf

towarddatascience - https://towardsdatascience.com/denoising-autoencoders-explained-dbb82467fc2

You May Also Enjoy