0. Generative Model
우리가 통계학의 기본에서 배우는 대부분의 모델들은 Discriminant Model이다. 통계학적으로 표현하자면 $Pr(Y \mid X)$이며 이것이 가정하는 상황은 X 데이터를 알때 Y 데이터의 확률을 구하는 것이라고 말할 수 있다.
그러나 이와는 다르게 Generative Model이라는 개념을 이야기 할 수 있다. 이를 통계학적으로 표현하자면 $Pr(Y,X)$이며 X와 Y 간의 정보에 대한 위계가 없는 상황을 가정하는 것이라고 말할 수 있다.
이는 인풋 데이터에도 자연 확률적인 요소를 넣은 개념이라고 볼 수 있고, Data Generating Process 그 자체를 추정하고자 하는 개념이라고 생각할 수 있다.
더욱이 Discriminant Model을 $Pr(Y\mid X) = \frac{Pr(Y,X)}{Pr(X)}$로 표현할 수 있으므로 좀 더 일반적인 모델이라고 말할 수 있다.
수학적으로는 둘의 차이를 명확하게 알 수 있지만, 실용적으로 어떤 차이가 있는지는 생각하기 힘들다. 좀 더 생각해보자. 만약 이 Generative Model을 추정해낸면 인풋 X를 알때 그와 동등한 위계를 가지는 X’를 확률적으로 만들어 낼 수 있다.
이를 통해 결측치를 채워 넣을 수도 있지만 그보다 좀 더 팬시한 사용처로 인공적으로 사진이나 문구 등을 만들어 낼 수도 있다. Generative Model을 이용해 X’을 생성해내는 방식은 다음과 같다.
- 주어진 데이터 X에 대해 잠재변수 $\theta$의 분포 $Pr(\theta \mid X)$ 를 임의로 추정한다 .
- $Pr(\theta \mid X)$ 를 이용해 $Pr(X,\theta)$를 추정해낸다.
- 이를 이용해 새로운 데이터 생성 모델 $Pr(X’ \mid \theta)$를 역산해낸다.
- 역산해낸 분포를 이용해 새로운 X를 발생시킨다.
이러한 발생모델을 찾아내는 기법으로 유명한 것에는 AutoEncoder와 GAN이 있다. 이번 포스팅 시리즈에서는 다음과 같은 이야기들을 해보려고 한다.
A. Generative Model과 AutoEncoder의 General Preview
B. Regularized Autoencoder
C. Variational Autoencoder
D. Generative Adversary Network
E. Normalizing Flow
1. AutoEncoder의 개념
AutoEncoder는 1980년 Hinton이 “Backpropagation Without a Teacher”이라는 아이디어 아래서 제안된 기법이다. Teacher라고 함은 머신러닝의 Supervised Learning의 타깃을 의미하는 것이므로 Teacher 없는 Backpropagation이라 함은 타깃값이 없이 X 그 자체가 타깃이 되는 형태의 모델을 의미한다.
즉 Autoencoder는 비지도학습의 일환으로써 인풋 X를 받아 아웃풋 X를 반환하는 모델이라고 말할 수 있다. 이는 당시에는 그럴듯한 결과물을 내지 못했지만 2006년경 딥러닝의 발달로 유의미한 결과를 낼 수 있게 되었다.
AutoEncoder가 직접적으로 목표로 하는 것은 데이터를 효과적으로 코딩하는 것에 있다. 컴퓨터 과학에서 머신러닝을 바라볼때, 날 것의 데이터 R에서 목표값 Y를 가장 잘 설명해주는 R의 속성, Feature X를 찾는 것을 이야기 하곤 한다.
이를 알고리즘으로 반자동으로 찾아내게끔 하는 것을 Feature Learning이라고 이야기하며, 기본적인 Deep Neural Network에서는 히든 레이어들이 그 역할을 한다고 말할 수 있다.
Autoencoder도 이러한 맥락에서 바라본다면, 데이터 X를 가장 잘 효율적으로 잘 표현해주는 $\theta$ 로 매핑하는 것 즉, Data Encoding을 함으로써 Feature Learning을 하는 것이라고 말할 수 있다.
통계학적으로 AutoEncoder를 바라보면 복잡도가 큰 데이터를 그보다 낮은 차원으로 정보량 손실을 최소화 하면서 매핑하는 것, 즉 차원축소와 연결시킬 수 있다. 물론 AutoEncoder는 차원축소 후 원본 데이터 복원의 과정도 포함하는 것이므로 잠재변수로의 매핑이 최종목적은 아니다.
AutoEncoder는 차원축소와 발생모델에서 사용할 수 있으며 구체적으로 정보검색, 이상 징후 감지, 이미지처리 및 텍스트 분석의 영역에도 사용할 수 있다고 한다. 또 중요한 적용 예로 AutoEncoder를 활용해서 화학과 생물학의 분자 단위의 새로운 물질을 제안할 수 있다고 한다.
AutoEncoder의 일반적인 프레임워크는 다음과 같다.
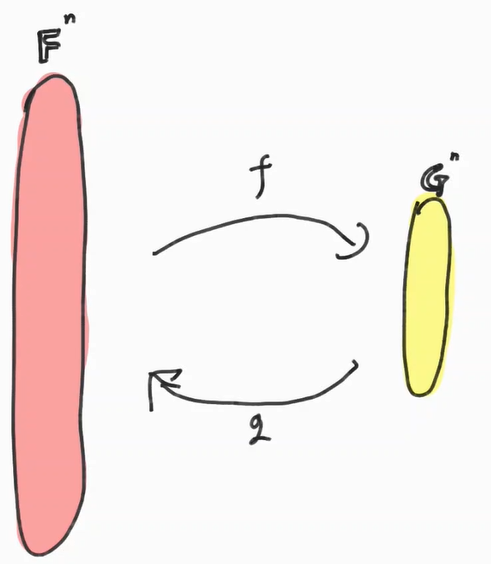
Autoencoder를 구성하는 요소는 $n,p,f,g,\mathbb{F},\mathbb{G},\Delta$가 있다. 그에 대한 설명은 다음과 같다.
-
$\mathbb{F}$ : Input과 Ouput Element가 존재하는 공간
-
$\mathbb{G}$ : Latent Element (or Code)가 존재하는 공간
-
$n,p$ : 각각 $\mathbb{F},\mathbb{G}$의 차원. 일반적으로 n>p 이며 인풋에 비해 적은 Latent Space차원을 써서 데이터를 만드는것이 목적일 때가 많다.
-
$f:\mathbb{F}^n \rightarrow \mathbb{G}^p$ : Real Space를 Latent Space로 맵핑해주는 함수 (Encoder)
-
$g:\mathbb{G}^p \rightarrow \mathbb{F}^n$ : Latent Space를 Real Space로 맵핑해주는 함수 (Decoder)
-
$\Delta$: Input과 Output 간의 차이를 재는 오차 함수
여기서 특히 $f,g$에 어떤 함수가 들어가는지와 $\mathbb{F},\mathbb{G}$를 어떤 공간으로 정의할 것인지에 따라 Linear Autoencoder, Boolean AutoEncoder, Neural Network Autoencoder 등의 종류로 갈린다.
이에 대한 목적함수는 다음과 같다.
$\underset{f,g}{\min} E(f,g) = \sum_{t=1}^n \Delta ((g \circ f)(x_t) , x_t)$
즉 손실 함수를 최소화 하는 함수를 찾는 것이 목적이 된다.
2. Linear AutoEncoder
Linear AutoEncoder는 단순 Linear Operation으로 $f,g$를 정의한다. 그렇기 때문에 다음과 같은 문제의 Setting을 가진다.
- $\mathbb{F} = \mathbb{G} = \mathbb{R}$
- $f = B \quad (p \times n \mbox{ matrix})$
- $g = A \quad (n \times p \mbox{ matrix})$
문제를 이렇게 Setting 한다면 결국 $\hat x = AB x$로 둔 것과 마찬가지이다. 따라서 문제를 다음과 같이 쓸 수 있다.
$\underset{A,B}{\min} \Delta (ABx,x )$
이 문제에 대해 $\Delta$를 L2 Norm으로 둘 시 다음과 같이 적을 수 있다.
$\parallel ABx-x \parallel = \parallel (AB-I)x \parallel$
이는 AB가 Fullrank가 아니기 때문에 Convex Function이 아니다. 그러나 A나 B 둘 중 하나를 고정시킨다면 단순 Affine Function이 되기 때문에 Convex Function이다. 따라서 반복적으로 추정하는 방식을 사용한다면 Minima를 찾아나갈 수 있다.
또 전체 목적함수는 Convex Function은 아니지만 Local Minima를 가지지 않는다.
$\min \parallel ABx - x\parallel_2^2$
이에 대한 Optimal Function A,B는 놀랍게도 PCA의 그것과 일치한다.
아래는 그에 대한 내용이다.
claim)
$\min \parallel ABx-x \parallel_2^2 =\min \parallel AA^{+}x-x \parallel_2^2 $
A를 고정 시켰을때 B에 대한 미분값을 0으로 만드는 B는 A의 Moore-penrose pseudoinverse 이다.
$f(A,B)= f_A(B) = \parallel ABx-x\parallel_2^2$
$\frac{\partial f_A(B)}{\partial A} = 1^t(ABx-x)\frac{\partial ABx}{\partial B} = 0$
우변은 $p \times n$ 행렬으로 $n \times 1$ 벡터를 미분하는 꼴인데 위키피디아의 행렬미분 항목을 참고해보니 모두가 동의할만한 이론이 정립되지 않았다고 한다.
그러나 꼴이 매우 단순한 만큼 A의 영향력은 모두 제거되어서 우변을 통해서 0을 만드려면 A=0인 trivial한 Case에서만 가능할 것이라고 생각된다.
그렇다면 좌변이 0이 되면 될텐데 결국 $ABx=x$를 만족해야 함을 알 수 있다.
non-trivial한 x에 대해서 위의 식이 성립하려면 AB = I에 준하는 꼴이 나와야하며 $B=A^{+}$(Moore - Penrose Pseudoinverse)일때가 가장 적합하다고 말할 수 있다.
위의 내용에 대한 구체적인 논문을 찾아보았지만, 그다지 엄밀한 증명이 포함되진 아니었다. 물론 직관적으로는 곧바로 연결할 수 있지만 설명이 충분하지 못한것은 아쉽다..
Moore-Penrose Pseudoinverse는 unique하게 존재하며 SVD를 통해서 $A = \Gamma \Lambda \Delta^t$에 대한 pseudo-inverse는 $A^{+} = \Gamma \Lambda^{-1}\Delta^t = (A^TA)^{+}A^T$로 정의될 수 있다. 이 결과를 함께 사용하면 다음과 같은 결과를 얻을 수 있다.
$= \min \parallel A(A^TA)^+A^Tx-x \parallel_2^2$
즉, x를 C(A)에 Orthogonal Projection 시킨 것과 같은 형태라고 볼 수 있다. 위의 Orthogonal Projection 함수의 랭크를 낮추고 $X^TX$의 Spectral Decomposition을 사용함으로써 AutoEncoder를 완성할 수 있다.
구체적으로 $X (n \times p)$ 행렬에 대해 $X^tX = \Gamma \Lambda \Delta^t$로 분해한 후 $\Gamma = (\Gamma_1 , \Gamma_2), A=\Gamma_1, B= \Gamma^t$ ,($\Gamma_1,\Gamma_2$ 는 각각 $n\times r , n \times (p-r)$ 행렬)으로 설정하면 된다.
예전에 사진파일을 넣으면 그를 SVD한 뒤 차원축소 후 재구성해주는 어플리케이션을 만든적이 있었는데 당시에는 그것이 AutoEncoder를 한 것인 줄은 모르고 있었다. 아래는 차원을 낮추는 Linear AutoEncoder를 진행한 예시가 되겠다.
3. Neural Net Autoencoder
사실 linear Autoencoder는 algebric하게 직관적인 함수를 설정할 수 있다는 장점이 있지만, 역시나 가정사항이 너무나 많아서 그리 효율적이라고 말하기는 어렵다.
가장 일반적인 Autoencoder의 목적함수에 대해서 제약을 둔것이나 마찬가지 이기 때문이다. 즉 다음과 같다.
일반적인 Autoencoder
$\underset{f,g}{\min} E(f,g) = \sum_{t=1}^n \Delta ((g \circ f)(x_t) , x_t)$
Linear AutoEncoder
$\ \underset{f,g}{\min} E(f,g) = \sum_{t=1}^n \Delta ((g \circ f)(x_t) , x_t) \\ \mbox{subject to }\begin{cases} \ f : \mbox{Linear Operator n to p} \\ g : \mbox{Linear Operator p to n} \end{cases}$
일반적으로 함수 공간의 다양성을 생각할때 위와 같은 문제를 일반화된 Autoencoder를 최적화 하기 위한 함수를 찾는 것은 어렵다고 말할 수 있다. 그러나 최근에는 만능해결책으로 딥러닝을 encoder,decoder 함수로 사용해서 유사 최적함수를 찾아낼 수 있다. 이 경우 다음과 같다고 말할 수 있다.
$\ \underset{f,g}{\min} E(f,g) = \sum_{t=1}^n \Delta ((g \circ f)(x_t) , x_t) \\ \mbox{subject to }\begin{cases} \ f(x) \equiv \mbox{NeuralNet}_1(x) \\ g(z) \equiv \mbox{NeuralNet}_2(z) \end{cases}$
이때의 Loss Function은 경험적으로 최적값을 가진다고 말해진다. 아래는 그에대한 성능의 비교이다.
제일 위는 원본 자료이고 두번째는 30차원으로 한정지은 Neural-Net Autoencoder, 제일 아래는 Linear Autoencoder이다. 두번째와 세번째의 차원이 같은것을 감안한다면 한눈에 보기에도 딥러닝의 효율성을 파악할 수 있다.
여기까지 기본적인 AutoEncoder에 대해서 알아봤다. 다음 포스팅에서는 Auto Encoder의 Variation에 대해서 알아보자.
참고 자료:
Pierre Baldi. Autoencoders, Unsupervised Learning, and Deep Architectures(2012)
위키피디아 - https://en.wikipedia.org/wiki/Autoencoder
손진원 선배님의 블로그 - https://jinwonsohn.github.io/lecture/2020/01/10/Bayesian-Inference.html
Elad Plaut.From Principal Subspaces to Principal Components with Linear Autoencoders(2018)
토론토 대학교 CSC321 강의자료 - http://www.cs.toronto.edu/~rgrosse/courses/csc321_2017/slides/lec20.pdf