[Non-linear Dimension Reduction] Part 3. Central sigma-Field for Nonlinear SDR and GSIR

Non-linear Dimension Reduction - 3. Central Class for Nonlinear SDR and GSIR

1. Nonlinear SDR Space

앞선 Linear SDR 분석에서는 다음과 같은 프레임워크를 취했다.

Assumption of conditional independence given linear SDR space: There is a \(\beta \mbox{ such that }Y \perp X \mid \beta^t X\) which means for the linear connection between Y and X, \(\beta^t X\) is sufficient to estimate Y

SDR space : $S =span(\beta;X \perp Y \mid \beta^tX)$$

Central Space : \(S_{Y\mid X} =\cap \{ S \mid S \mbox{ is SDR subspace}\}\)

Nonlinear의 범위에서 우리는 \(\beta^tX\)의 표현을 \(f (X)\)로 일반화시키는 것을 목표로 한다. 따라서 우리가 찾고자 하는 관계성은 \(Y \perp X \mid f(X)\)로 변한다. 이 말인 즉슨, Y를 예측하는데에 있어 X를 어떠한 함수에 통과시켜서 얻어낸 값만 알면 나머지 정보는 필요없음을 의미한다.

확률 공간에서는 이 특정 함수값 f(X)를 X를 통해서 만들어진 시그마 필드 \(\sigma(X)\)로 일반화 할 수 있다. 따라서 SDR subspace는 SDR \(\sigma\) - field로 확장된다.

SDR \(\sigma\) - field : A sub \(\sigma\)- field \(\mathfrak{g}\) of \(\sigma(X)\) which satisfies \(Y \perp X \mid \mathfrak{g}\).

여기서 추가적으로 SDR \(\sigma\) - field 중에서도 가장 작은 \(\sigma\) - field를 Central \(\sigma\)-field라고 부른다. 사실은 이러한 가장 작은 sigma field가 존재하느냐에 대한 존재성의 증명을 보여야 겠지만, 증명에 사용되는 개념이 너무 생소해서 관뒀다.

Central \(\sigma\) - field: \(\mathfrak{g}_{y\mid x} = \cap \{\Sigma \mid \Sigma \mbox{ is SDR }\sigma \mbox{- field}\}\)

여기에 더해 추가적으로 Complete \(\sigma\) - field라는 개념이 있다. 이 역시 생소한 내용이 성질로써 포함된다.

Complete \(\sigma\) - Field : A sub \(\sigma\) - field of \(\sigma(X)\) is complete if, for any g-measurable \(f, E(f(X) \mid \mathfrak{g})\) = constant almost surely \(\Rightarrow E(f(X) \mid Y) =\)constant almost surely

다행히도 이 두가지 컨셉은 매우 완화된 조건이라 체크할 필요성이 거의 없다.

이렇게 \(\sigma\) - field 단위에서 SDR field를 정의했지만 \(\sigma\)- field는 너무 추상적인 개념이라 직접적으로 발전 시키기 어렵다. 따라서 이를 앞에서 정의했던 RKHS 공간으로 전이한다면 행렬과 벡터 시스템에서 분석을 할 수 있다.

\(H_x\)를 X를 인풋으로 가지는 functional들의 집합이라고 하자. 이에 대해 다음과 같은 \(f_1,f_2 ,... f_d \in H_x\)를 가정할 수 있다.

\[Y \perp X \mid f_1(X),f_2(X),...,f_d(X)\]

이 경우 Central \(\sigma\) - field는 \(\sigma(f_1(X),f_2(X),...,f_d(X))\)이다.

이에 대해서 \(H_x(\mathfrak{g}) = \bar{span} \{f \in H_x : f \mbox{ is measurable on } \mathfrak{g}\}\)를 정의하자. \(f\)가 \(\mathfrak{g}\)에 measurable하다는 의미는 \(\mathfrak{g}\)에서 함수값들이 정의가 다 되어 있다는 것을 의미한다.

따라서 개중 Central \(\sigma\) - field에 대응되는 RKHS도 정의할 수 있다. 이를 Central Class라고 부르며 우리의 메인 타깃이 된다.

Central Class \(\mathfrak{G}_{y \mid x}\): \(H_x(\mathfrak{g_{y \mid x}})\)

이러한 Central Class를 예측함에 있어서 candidate operator \(T(F_0)\) where \(F_0\) is distribution function of X를 추정하는 \(T(F_n)\)을 정의할 수 있고, 이에 대해서 만약 \(\bar{ran}(T(F_0)) \subset \mathfrak{G}_{y \mid x}\)일시 \(T(F_n)\) 을 unbiased estimate라고 부르고 \(\bar{ran}(T(F_0)) = \mathfrak{G}_{y \mid x}\) 일시 exhaustive estimate라고 부른다.

여기까지 컨셉에 대해서 정리해봤다. 아무래도 추상적인 개념들 위주로 다루기 때문에 생소할 수 있다. 실제로 이 Central Class를 추정해주는 알고리즘인 GSIR에 대해서 알아보자.

2. Generalized Sliced Inverse Regression

A. GSIR의 이론적 증명

Regression Analysis \(Y = X\beta\)에서 \(\beta\)의 추정치는 \((X^tX)^{-1}X^tY\)이다. 이 형태는 X와 Y가 centered 되어 있다는 가정 아래서 \(\Sigma_{xx}^{-1} \Sigma_{xy}\)의 형태와 일치한다.

\(GSIR\)에서는 이 추정 행렬 \(\Sigma_{xx}^{-1}\Sigma_{xy}\)를 operator로 확장해서 해석한다. 즉, \(\bar{ran}(\Sigma_{xx}^{-1}\Sigma_{xy}) \subset \mathfrak{C}_{y \mid x}\)가 성립하기에 \(\Sigma_{xx}^{-1} \Sigma_{xy}\)를 센트럴 클래스에 대한 candidate matrix로 사용할 수 있다.

그러나 이 정리가 성립하려면 Linear SIR의 LCM condition과 비슷하게 4가지 가정을 만족해야 한다. 그러나 이 가정들은 매우 마일드한 가정이기 때문에 LCM보다 만족하기가 쉽다.

GSIR의 가정들

1. \[E(k(X,X)) < \infty\]
2. ker(\(\Sigma_{xx}\)) = {0}
3. \(ran(\Sigma_{xy}) \subset ran(\Sigma_{xx})\), \(ran(\Sigma_{yx}) \subset ran(\Sigma_{yy})\)
4. \(\Sigma_{xx}^{-1}\Sigma_{xy}\) and \(\Sigma_{yy}^{-1} \Sigma_{yx}\) is compact operator.

첫번째 가정은 힐버트 공간의 mean operator와 covariance operator가 잘 정의 되게끔 만들어주는 가정이다. 일반적으로 사용하는 커널과 상식적으로 발생하는 확률변수는 해당가정을 대부분 만족한다.

두번째 가정은 \(\Sigma_{xx}^{-1}\)을 정의하기 위해 사용하는 가정이다. 이는 RKHS를 \(ran(\Sigma_{xx})\)로 재 정의함으로써 만족시킬 수 있다.

세번째 가정은 \(\Sigma_{xx}^{-1} \Sigma_{xy}\)를 정의하기 위해 사용되는 가정이다. 이때, \(ran(\Sigma_{xy}) \subset \bar{ran}(\Sigma_{xx}) ,ran(\Sigma_{yx}) \subset \bar{ran}(\Sigma_{yy})\)가 성립하는 것은 알려져있기 때문에 해당 가정 역시 약한 가정이라고 볼 수 있다.

네번째 가정은 \(\bar{ran}(\Sigma_{xx}^{-1}\Sigma_{xy})\)를 compact set으로 만들기 위한 가정이다. \(\Sigma_{xx}\)는 0으로 수렴하는 아이젠 밸류 수열을 가진 operator 이므로 그 역함수는 필연적으로 unbounded하다. 그러나 \(\Sigma_{xy}\)의 range가 0으로 수렴하지 않는 아이젠밸류에만 한정된다고 가정하면 \(\Sigma_{xx}^{-1}\)를 bounded하게 만들 수 있다.

여기에 더해 다음 렘마가 성립한다.

Lemma

If \(H_x\) is dense in \(L_2 (P_y)\) modulo constants. Then for any \(f \in H_x\), \(\Sigma_{yy}^{-1} \Sigma_{yx}f = E(f(X) \mid Y) + constant\) i.e. \(cov(f(X) - (\Sigma_{yy}^{-1}\Sigma_{yx} f)(Y) , g(Y) ) = 0\) where \(\forall g \in L_2(P_y)\)

이를 이용해서 GSIR Theorem을 증명해보자.

Theorem - GSIR

Suppose above 4 assumptions are hold, and \(\mathfrak{G}_{y \mid x}\) is dense in \(L_2(P_x \mid \mathfrak{g}_{y \mid x})\) modulo constants, then \(\bar{ran} (\Sigma_{xx}^{-1}\Sigma_{xy}) \subset \mathfrak{G}_{y \mid x}\)

---

pf)\(\def\inn#1{\left< #1\right>}\)

우선 \(\bar{ran}(\Sigma_{xy}) \subset \Sigma_{xx} \mathfrak{G}_{y \mid x}\)을 보이자.

Let \(f \in (\Sigma_{xx} \mathfrak{G}_{y \mid x})^{\perp}\) and \(g \in \mathfrak{G}_{y \mid x}\), then \(\inn{f , \Sigma_{xx}g} = cov(f(X),g(X)) =0\).

함수 g는 \(\mathfrak{G}_{y \mid x}\)에 있으므로 \(g(X) = E(g(X) \mid \mathfrak{g}_{y \mid x})\)가 성립한다.

따라서 \(cov(f(X),g(X)) = cov(f(X),E(g(X)\mid \mathfrak{g}_{y \mid x}) = cov(E(f(X)\mid \mathfrak{g}_{y \mid x}),g(X))\)이다.

여기서 \(\mathfrak{G}_{y \mid x}\)는 \(L^2(P_y)\)에 대해서 dense하므로 \(cov(E(f(X) \mid \mathfrak{g}_{y \mid x}),E(f_n(X) \mid \mathfrak{g}_{y \mid x})) \rightarrow var(E(f(X) \mid \mathfrak{g}_{y \mid x})=0\)이 성립한다.

따라서 \(E(f(X) \mid \mathfrak{g}_{y \mid x}) = constant\) a.s.P 이다.

또한 \(E(f(X) \mid \mathfrak{g}_{y \mid x}) = E(f(X) \mid Y,\mathfrak{g}_{y \mid x}) = E(f(X) \mid Y) = constant \quad a.s.P\)가 성립한다.

(\(\mathfrak{g}_{y \mid x}\)의 sufficient한 성질을 이용하여)

이 결과와 Lemma를 결합하면 \(\Sigma_{yy}^{-1} \Sigma_{yx}f = constant\)라는 결론을 얻을 수 있다. \(ran(\Sigma_{yy})\)에 존재하는 constant는 0이 유일하다. 따라서 \(f \in ker(\Sigma_{yx})\)이다.

정리하면 \(f \in (\Sigma_{xx} \mathfrak{G}_{y \mid x})^{\perp} \rightarrow f \in ker(\Sigma_{yx}) = ran(\Sigma_{yx})^{\perp}\)이므로 \((\Sigma_{xx} \mathfrak{G}_{y \mid x})^{\perp} \subset ran(\Sigma_{yx})^{\perp} \Rightarrow ran(\Sigma_{yx}) \subset \Sigma_{xx} \mathfrak{G}_{y \mid x}\)

\[\Sigma_{xx}^{-1} ran(\Sigma_{xy}) = \{\Sigma_{xx}^{-1} f : f = \Sigma_{xy}g , g \in H_{y}\}\]

​ \(= \{\Sigma_{xx}^{-1}\Sigma_{xy} g , g \in H_y\} = ran(\Sigma_{xx}^{-1}\Sigma_{xy}) \qquad \qquad \qquad \square\)

---

B. GSIR의 구현

PIR과 유사하게, ran(\(\Sigma_{xx}^{-1}\Sigma_{xy}\))를 좀 더 쉽게 구하기 위해 non-singular A에 대해 \(ran(\Sigma_{xx}^{-1} \Sigma_{xy} A \Sigma_{yx}\Sigma_{xx}^{-1})\)를 대신 구할 수 있다.

이는 곧 다음과 같은 문제로 변한다.

\[\max \inn{f ,\Sigma_{xy} A \Sigma_{yx}}\] \[\mbox{subject to } \inn{f , \Sigma_{xx} f} =1\]

따라서 이 문제는 \(GEV(\Sigma_{xy} A \Sigma_{yx} , \Sigma_{xx})\)로 변한다. A operator는 주로 \(I\)나 \(\Sigma_{yy}^{-1}\)로 제안된다.

KPCA와 마찬가지로 샘플 레벨에서는 함수를 RKHS에서 해석하여 Coordinate Mapping을 하여서 구현한다. 이를 직접 살펴보자.

\[\def\coor#1#2{\left[#1\right]_{\mathfrak{#2}}}\] \[\max \inn{f, \hat{\Sigma}_{xy}A \hat{\Sigma}_{yx}f}_{Hx} = \coor{f}{Bx}^t G_x (_{\mathfrak{B}_x} \coor{\hat{\Sigma}_{xy}}{By})(_\mathfrak{By}\coor{A}{By})(_\mathfrak{By}\coor{\hat{\Sigma}_{yx}}{Bx})\coor{f}{Bx}\]

​ \(= \coor{f}{Bx}^t G_x G_yAG_x\coor{f}{Bx}\)

\[\mbox{subject to }\inn{f, \Sigma_{xx} f} = \coor{f}{Bx}^t G_x (_\mathfrak{By}\coor{\hat{\Sigma}_{xx}}{Bx}) \coor{f}{Bx} = \coor{f}{Bx}^t G_x^2 \coor{f}{Bx}\]

A=I 일때

여기서 A가 I일때는 다음과 같은 문제로 변형이 된다.

\[\max \coor{f}{Bx}^t G_x G_yG_x\coor{f}{Bx}\] \[\mbox{subject to } \coor{f}{Bx}^t G_x^2 \coor{f}{Bx}\]

이는 \(GEV(G_xG_yG_x , G_x^2) = GEV(G_x^{-1} G_x G_y G_x G_x^{-1} ,I)\)이다.

여기서 문제가 발생하는데, \(G_x\)는 \(QKQ\)의 형태로 \((I-\mu)\)의 공간으로 사영되므로 무조건 singular matrix라는 점이다. 따라서 해당 문제에서는 pseodo-inverse를 사용해 주어야 하는데 일반적으로 사용하는 moore-penrose inverse \(G_x^{+}\) 대신 오버피팅도 함께 잡아주는 Tychonoff-regularized Inverse \((G_x +\eta_x I_n)^{-1}\)를 사용해준다.

여기서 \(\eta\)가 너무 크면 문제가 발생하므로 적절한 값을 찾아줘야 하는데, 이에 대한 적정값은 아직 미지의 영역이며 현재로선 Cross Validation을 통해 찾아주는 것이 일반적이다.

따라서 최종적으로 문제는 \(GEV(\Lambda^{(1)}_{GSIR}); \Lambda_{GSIR} = (G_x + \eta_xI_n)^{-1} G_x G_y G_x (G_x + \eta_x I_n)^{-1}\)가 된다.

A = \(\Sigma_{yy}^{+}\)일때

위와 마찬가지로 pseudo-inverse를 사용해주어야 하며 이 경우 문제는 \(GEV(\Lambda_{GSIR}^{(2)}) = (G_x + \eta_x I_n)^{-1} G_x G_y (G_y +\eta_y I_n)^{-1} G_x (G_x +\eta_x I_n)^{-1}\)이 된다.

우리는 어디까지나 거대한 추정량을 찾아나가는 것이기 때문에 계산 과정에서의 방법에 민감하게 반응한다. 따라서 두 가지 선택은 이론상 결과가 같아야 함에도 불구하고 제법 다른 결과가 나온다. A=I일 경우 적은 샘플에서 더 잘 작동한다는 실험 결과가 있지만 역시 데이터의 형태에 따라서 천차만별의 결과가 나올것으로 생각된다.

실제 구현은 다음과 같이 진행된다.

---

Algorithm. GSIR

---

1. X,Y를 표준화한다.
2. 그람 행렬을 계산한 후, 각종 하이퍼 파라미터를 찾아준다.
3. 위의 행렬에 대해서 Spectral Decomposition을 해줘서 축 \(v_i\)를 찾아준다.
4. 위에서 \(\coor{f_i}{Bx} = (G_x +\eta_x I_n)^{-1}v_i\)이며 \(f_i(X) = \coor{f_i}{Bx}^t\{ K(X,X_i)\}_i\)가 된다.

---

GSIR에서는 X 커널,Y 커널 두개가 필요하다. 커널의 선택에 있어서 최적화 상의 차이점들은 있겠지만 알려져있는 커널들은 거의 dense modulo constant하므로 이론상으로는 대동소이하다.

Continuous Kernel에서 가장 많이 쓰이는 커널은 Gaussian Kernel이고 Discrete kernel에서 가장 많이 쓰이는 커널은 Kroneckor Delta Kernel이다. 이를 이용해서 구현해보자.

def stand(x) : return(np.matmul(x-np.apply_along_axis(np.mean,0,x),np.diag(np.apply_along_axis(np.var,0,x))))
def matpower(mat,power,thre):
    eig = np.linalg.eig(mat)
    val = np.diag([np.real(i**power) if i >thre else 0 for i in eig[0]])
    vec = np.real(eig[1])
    return(np.matmul(np.matmul(vec,val),vec.T))

def Gram_gaussian(data,comp) : 
    n = data.shape[0];p = data.shape[1] 
    U = np.matmul(data,data.T)
    M = np.outer(np.diag(U),np.ones(shape=(n,1)))
    J = np.outer(np.ones(shape=(n,1)),np.ones(shape=(n,1)))
    Q = np.identity(n)-J/n
    K = M+M.T-2*U
    sigma = (np.sum(np.sqrt(K))-np.trace(np.sqrt(K)))/n/(n-1)
    gamma = comp/sigma/sigma
    return(np.matmul(Q,np.exp(-K*gamma),Q))

def Gram_discrete(data) :  
    n = data.shape[0]
    J = np.outer(np.ones(shape=(n,1)),np.ones(shape=(n,1)))
    Q = np.identity(n)-J/n
    dis = np.matmul(np.matmul(Q,[[1 if i==j else 0 for j in data] for i in data]),Q)
    return(dis)

KPCA와 마찬가지로 필요한 함수들을 미리 지정해주자.

def KPCA(X,comp,thre = 10**(-8)) :
    X = stand(X)
    G = Gram_gaussian(X,comp)
    eig = np.linalg.eig(G)
    V = np.real(eig[1])
    U = np.matmul(matpower(G,-0.5,10**(-8)),V)
    return(np.matmul(G,U))
def GSIR(y,X,comp):
    X = stand(X)
    n = X.shape[0];p = X.shape[1] 
    G_y = Gram_discrete(y)
    G_X = Gram_gaussian(X,comp)
    Ginv = np.linalg.pinv(G_X)
    candi_matrix = np.matmul(np.matmul(np.matmul(np.matmul(np.matmul(Ginv,G_X),G_y),Ginv),G_X),Ginv)
    eig = np.linalg.eig(candi_matrix)
    V = np.real(eig[1])
    return(np.matmul(np.matmul(G_X,Ginv),V))

앞선 포스팅에서 만들었던 KPCA 예시와 함께 비교해보자.

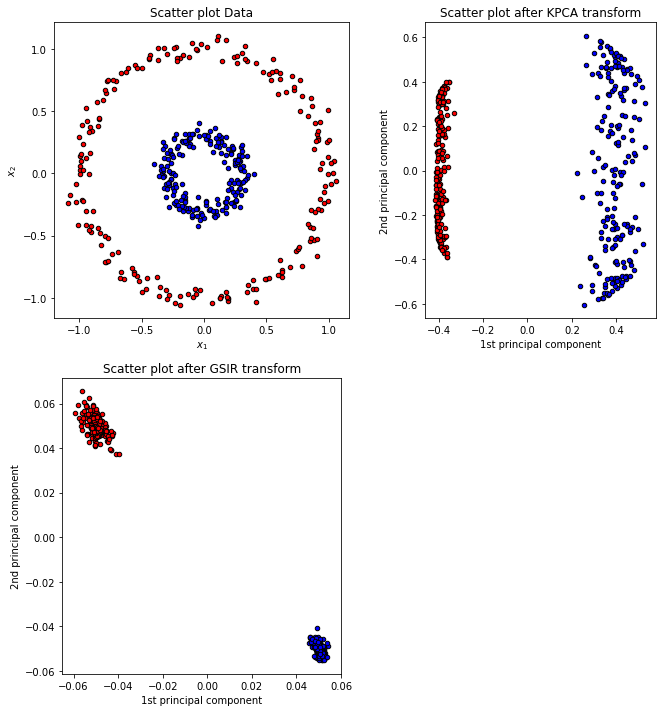
KPCA는 Y값의 정보가 있지 않은 반면 GSIR에는 Y값이라는 정보가 있다. 그렇기 때문에 GSIR의 효과가 극적으로 나타난 것이라고 생각할 수 있다.

추가적으로 해당 알고리즘에는 커널의 하이퍼파라미터에 민감하기에 이를 잘 찾아줘야 한다.

여기까지 GSIR에 대해서 알아보았다. 다음 포스팅에서는 SAVE의 nonlinear버전인 GSAVE에 대해서 알아보도록 하자.

---

Debnath, L.& Mikusinski, P. (2005). Introduction to Hilbert Space.London,UK.:Elsevire Academic Press
Li, B. (2018). Sufficient Dimension Reduction. Boca Raton,FL:CRC Press.