0. 개요
Matrix Factorization은 행렬을 주요 요인으로 분해한다는 개념으로, 천문학,화학,자연어 처리, 사운드 분석, 추천 시스템 등에서 다양하게 응용되는 개념이라고 한다.
앞서 포스팅한 PCA나 군집분석과는 다르게, 이번에는 좀 더 일반화된 개념부터 접근해서 행렬 분해의 전반을 공부 해보려고 한다.
현재까지 예정되어 있는 학습 내용은 다음과 같다.
Part 1. Bregmann Divergence
Part 2.Generalized Non Negative Matrix Factorizaion with Bregamnn Divergence
Part 3. Independent Component Analysis
Part 4. Incremental PCA, Kernel PCA, Sparse PCA
Part 5. Factorization Model
1. Independent Components Analysis란?
Signal과 Noise
통계학에서는 관측된 데이터는 Signal과 Noise 두 가지로 분해 될 수 있다고 보는 관점이 있다.
예를 들어 가장 간단한 회귀모델 $y_i =X_i \beta + \epsilon_i$ 를 생각해보자.
이를 통해 만들어진 데이터 $y_1 = X_1 \beta +\epsilon_1$은 똑같은 상황(똑같은 $X_1$)이 주어졌을 때의 데이터 $y_1’ = X_1 \beta + \epsilon_1’$와 $X_1\beta$부분은 같고 $\epsilon$부분은 다르다.
데이터 $y$를 분석하거나 예측할 때 일관성 있게 똑같이 나오는 부분이 분석이나 예측에 있어서 더 쉽게 해석되고, 중요한 직관을 가져다 줄것이다. 이 부분을 Signal이라고 부른다.
반면 계속해서 변화하는 부분은 포착이 불가능한 부분이고 분석이나 예측에 있어서 오히려 방해를 할 것이다. 이 부분을 Noise라고 부른다.
좋은 모델링은 Noise 부분에서 설명가능한 부분을 계속 찾아내서 Signal로써 포착 해내는 것이라고 말 할 수 있다. 게다가 Signal을 발산하는 Source를 최대한으로 찾아내고 분류해내는 것도 좋은 모델링이라고 할 수 있다.
ICA란?
많은 실제 관측자료는 위와 같이 Signal과 Noise가 섞여있다. 예를 들어, 길거리 버스킹을 녹음한 자료가 있을 때, 그 속에는 기타 소리, 보컬 소리, 드럼 소리 등의 Signal과 지나가는 사람들의 잡담, 발걸음, 자동차 소리 등의 Noise가 섞여있다.
이러한 섞여있는 자료를 다른 자료와 분리를 해내는 문제를 Blind Source Separation(BSS)라고 부른다. Blind가 의미하는 바는, 데이터에 대해서 그 데이터 이외의 외부 정보가 거의 없는 경우를 의미한다. 이러한 BSS 문제를 푸는 가장 대표적인 알고리즘이 바로 Independent Components Analysis이다.
ICA는 Data에서 Noise를 제외한 독립적인 Signal을 찾아내는 데 특화된 알고리즘이다. 따라서 위의 BSS 문제를 효과적으로 해결할 수 있을 뿐만 아니라, 영상 신호, 생체 인식 등에도 사용할 수 있다. 게다가, Signal을 잘 잡아내고 Noise를 잘 찾아낸다면 Dimensionality Reduction에도 사용할 수 있는 범용성 있는 알고리즘이다.
2.ICA의 이론적 배경
ICA는 통계적으로 독립적인 Factor를 뽑아내는 알고리즘이다. 이를 위해서 ICA는 아래 3가지에 집중한다.
- Factor의 비정규성의 극대화
- Factor간 공유 정보의 극소화
- Factor 추정의 Likelihood의 극대화
몇 가지는 납득이 되지만 납득이 되지 않는 것도 있을 것이다. 이에 대해서 자세히 알기 위해서는 Mixed Data의 특징에 대해서 알아야 한다.
Mixed Data에 대한 이해
Mixed Data에 대해서 이해하기 위해 아래와 같은 Notation을 적용해보자
$s_{ij}$는 i 신호의 j 번째 값을 의미한다. 이는 N time까지 기록되는 일종의 시계열 변수라고 해석할 수 있다.
이에 대해 다음과 같은 표기를 사용하자
이 두 가지 Signal 두 개의 인식장치에서 인식이 되었다고 가정하자. 그렇다면 센서의 위치에 따라서 다음과 같이 변화를 할 것이다.
이 A를 Mixing Coefficients Matrix라고 부른다.
이러한 구성을 토대로 아래와 같은 예시를 통해서 Mixed Data의 성질에 대해서 이해해보자
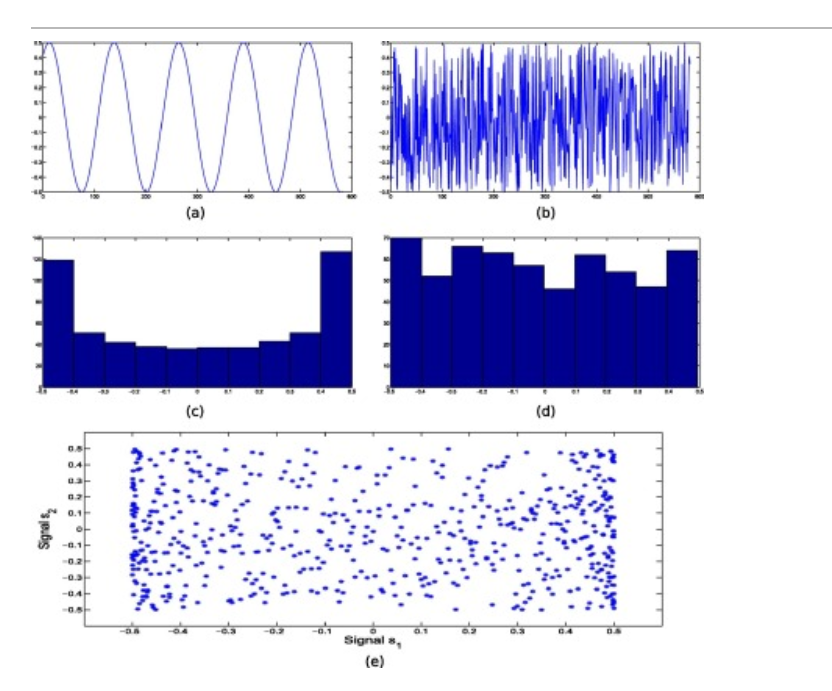
$\textbf{s}_1 = sin(a)$ ; $a \in [1,30]$
$\textbf{s}_2 = r-0.5$ ; $r \sim unif(0,1)$
아래 그림은 두 Signal $\textbf{s}_1,\textbf{s}_2$에 대한 시계열 그림과 히스토그램, 그리고 시간에 따른 산점도 이다.
- 시계열 그림이 비교적 덜 복잡함
- 히스토그램이 정규성을 띄고 있지 않음
- 산점도에 패턴이 보이지 않으므로 두 Signal은 독립이라고 말 할 수 있음
아래 그림은 두 Signal이 섞인 데이터 $\textbf{x}_1,\textbf{x}_2$에 대한 시계열 그림과 히스토그램, 그리고 시간에 따른 산점도이다.
- 시계열 그림이 복잡함
- 히스토그램이 정규성을 띄고 있음
- 산점도에 패턴이 나타나므로 $\textbf{x}_1,\textbf{x}_2$는 서로 연관이 있음
히스토그램에 정규성이 나타나는 이유는 CLT의 그것과도 관련이 있다. CLT는 개별 자료의 특성들이 다른 자료들에 묻혀 사라질때 정규분포를 따른다고 이해할 수 있는 데, 두 가지 자료가 믹싱됨으로써 개별 특성들이 사라지는 것이다. 산점도에 패턴이 나타나는 것은 당연한 일이다. 두 Sound가 Signal을 공유하기 때문이다.
위의 이해를 역으로 한다면, Mixed Data에서 뽑아낸 팩터들은 서로 통계적으로 독립이어야하고, 정규성을 띄어선 안되고, 또 최대한 단순해야 한다. 이것들이 ICA가 이를 제거하는 것을 목표로 삼는 이유이다.
ICA의 원리
위의 Notation을 그대로 사용하여서 알고리즘을 이해해보자. 시그널들이 $\textbf{s}_1=(1,2,1,1),\textbf{s}_2 = (1,1,2,2)$라고 가정하자. 이는 바로 관측될 수 있는 값이 아니라 Mixing을 거친다음에 관측될 수 있다. 이때의 Mixing Coefficients Matrix A가 형성하는 차원으로 Transformation되어서 관측된다고 해석 할 수 있다. 이때 Transformation 되는 축을 $\textbf{s}_1’,\textbf{s}_2’$이라고 정의하자. 이 축들은 관측공간인 X Space를 형성하게 된다.
이 관측 데이터에 대해 아래와 같은 수식을 생각해보자
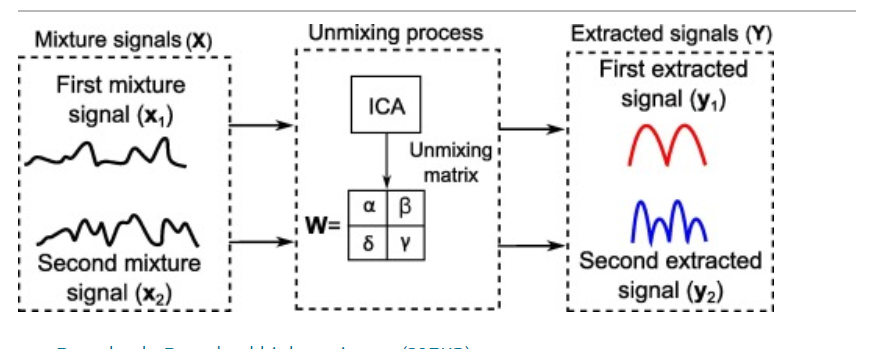
이는 Mixing된 데이터를 Unmix시키는 작업이라고 볼 수 있으며 이때 $\textbf{W} $는 Unmixing Matrix라고 정의되며 각 벡터들은 weight 벡터이다. 이렇게 추출된 $\textbf{y}_1,\textbf{y}_2$는 역산을 통해 Signal을 추정하는 추정 벡터라고 볼 수 있다. 이 Unmixing Matrix W를 찾는 작업이 바로 ICA이다.
Unmixing Matrix는 단순 계산하여 Mixing Matrix A의 역행렬이라고 얘기할 수 있지만, A와 S는 관측 될 수 있는 것이 아니기에 직접 찾을 수 없다. 그래서 차선책으로 A를 통해 transformation된 관측값들이 존재하는 축 $\textbf{s}_1’,\textbf{s}_2’ $에 각각 Orthogonal한 벡터들 $\textbf{w}_1,\textbf{w}_2$를 찾음으로써 $\textbf{W}\textbf{A} = \lambda I$의 관계를 따르는 Unmixing matrix $\textbf{W}$를 추정해낼 수 있다.
이 프로세스를 도식화 하면 아래와 같다.
그러나 이러한 방식으로 찾아낸 $\textbf{Y}$는 원본 Signal을 완전하게 복원 해낼 수는 없다. 그는 아래와 같은 이유 때문이다.
-
추출된 $\textbf{Y} $는 W의 크기(Length)에 영향을 받는다.
pf) $\textbf{W}^T = A^{-1}$일 때 $\textbf{y}_1 = (\lambda \textbf{w}_1^T)\textbf{X} = \lambda (\textbf{w}_1^T\textbf{X}) = \lambda \textbf{s}_1$ $;\lambda$는 상수
-
추출된 Y는 W의 방향(Orientation)에 영향을 받는다.
pf) $\textbf{y}_1 = \textbf{w}_1^T \textbf{X} = \textbf{w}_1^T \textbf{A} \textbf{S} = \textbf{w}_1^T(\textbf{s}_1’ \ \textbf{s}_2’)^T = \textbf{w}_1^T\textbf{s}_1’ $ ($\textbf{w}_1$과 $\textbf{s}_2’$는 orthogonal)
$= \mid \textbf{w}_1 \mid \mid \textbf{s}_1’ \mid cos \ \theta = \mid \textbf{w}_1 \mid \mid \textbf{A} \textbf{s}_1\mid cos \ \theta = k \textbf{s}_1$ $; k$는 상수
위의 두 식을 다시 보면 $\textbf{W}$의 크기와 방향이 모두 똑같은 방식 ($\lambda , k$)으로 영향을 준다. 따라서 결과물 $\textbf{Y}$에는 $\lambda$와 $k$의 영향이 섞여서 작용하게 되고 이 둘을 구별할 수 있는 방법은 없다. 따라서 정확한 Unmixing Matrix를 구하는 것은 불가능에 가깝고 어디까지나 추정만을 할 수 있다고 말 할 수 있다.
또한 ICA는 다음과 같은 한계를 내포하고 있다.
- 결과물 $\textbf{Y}$의 부호가 모호함 (- 결과물에 -1을 곱해도 프로세스상 똑같이 나온다.)
- Mixed Data $\textbf{X}$가 Signal 개수보다 적을시 A의 역 행렬이 존재하지 않음
3. ICA의 기준
그러나 이렇게 단순 역행렬을 추정하는 것이 ICA의 목적을 달성하게 하지는 않는다. 다시 상기시키면 ICA는 다음을 추구함으로써 독립 성분을 분석해낸다.
- Factor의 비정규성의 극대화
- Factor간 공유 정보의 극소화
- Factor 추정의 Likelihood의 극대화
따라서 역행렬의 열들이 위와 같은 원칙하에서 Factor를 형성해야 한다. 이를 위한 측정기준은 1. Kurtosis, 2. Negentropy, 3. Mutual Information Criterion이다. 하나씩 알아보자
A. Kurtosis
Kurtosis는 첨도라고 해석되며 분산보다 더 높은 차수를 가지는 통계량이다. 구체적으로 Kurtosis는 다음과 같이 정의된다.
$K(\textbf{y}) = E \left[ \left( \frac{X- \mu}{\sigma} \right)^4 \right] = E(\textbf{x}^4) - 3 [E(\textbf{x}^2)]$
이 알고리즘에서는 이를 약간 변형시킨 Excess Kurtosis 라는 것을 사용한다.
$K’(\textbf{y}) = \frac{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^4}{[\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2]^2}-3$
이는 단순히 Kurtosis에서 3을 뺀 것이다. 이렇게 평행이동을 해줘야 표준 정규분포의 Excess Kurtosis가 0이 나오기 때문이다. 아래는 Excess Kurtosis의 값에 따른 분포의 모양 변화에 대한 그림이다.
시각화 해서 보면 0에 가까울수록 정규성을 띄고 0에서 멀어질 수록 정규성을 띄지 않는다고 말 할 수 있다. 따라서 적절한 첨도값을 가지는 Unmixing Matrix W를 찾아내면 비정규성을 가지는 새로운 추출 신호 $\textbf{y}$를 찾아낼 수 있다고 말 할 수 있다.
그러나 이 기준은 아웃라이어에 취약하다는 단점이 있다.
B. Negentropy
Negentropy는 Negative Entropy의 준말로, 다음과 같이 정의된다.
$J(p_x) =S(\psi_x)-S(p_x)$
$S(p_x) = - \int p_x(u) log \ p_x(u) du$ (; Entropy)
$\psi_x$는 x와 평균과 분산이 같은 정규분포
즉 정규분포의 엔트로피와 표본을 통해 추정한 분포의 엔트로피의 차이라고 말할 수 있다. 평균과 분산이 같다면 엔트로피를 가장 크게 만드는 분포는 정규분포임이 증명되어있다. 따라서 Negentropy는 언제나 Nonnegative하다. 이 Negentropy를 Maximize하는 Factor $\textbf{y}$를 찾음으로써 목적을 달성 할 수 있다.
뱀발로, 샘플이 한정되어 있을때 Entropy를 정확히 계산하는 것은 어려운 일이다. 분포를 추정하기 위해서는 많은 샘플이 필요하기 때문이다. 따라서 아래와 같은 근사공식을 사용해 준다고 한다.
$J(\textbf{y}) \approx \frac{1}{12}E[\textbf{y}^3]^2 + \frac{1}{48} K’ (\textbf{y})^2$
이 공식을 잘 살펴보면 Negentropy와 Kurtosis가 결국 연결되어 있음을 알 수 있다.
C. Mutual Information Criterion
Mutual Information은 다음과 같이 정의된다.
$I(x,y) = \underset{x,y}{\sum}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$
$=S(x)+S(y) - S(x,y)$
이 식을 잘 보면 Joint PDF $p(x,y)$와 Marginal PDF의 단순곱 $p(x)p(y)$의 Kullback-Leibler Divergence임을 알 수 있다.
두 변수가 독립일때 Joint PDF는 Marginal PDF의 곱으로 나타나므로 두 PDF의 거리를 독립성 척도로 사용하는 것이다.
이 기준을 우리 문제에 적용하면 다음과 같은 공식이 도출된다.
$I(\textbf{y}_1,\textbf{y}_2,…,\textbf{y}_m) = C-\underset{i}{\sum}J(\textbf{y}_i)$ ;C는 상수
결국 Mutual Information도 Negentropy와 연결되어있음을 알 수 있다.
4. ICA 알고리즘
ICA 전처리
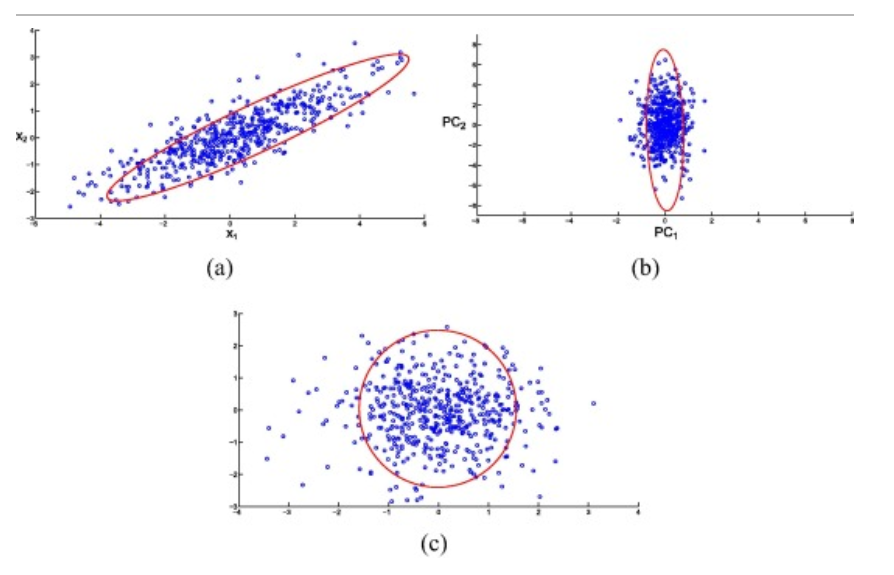
ICA를 하기에 앞서서 Observerd Data X를 PCA 해준 후 Scaling을 해줘야 한다.
이를 통해 얻는 결과물 행렬 Z는 다음과 같은 특징을 갖는다.
- $Z$의 축들은 모두 직교한다.
- $E(Z^TZ) = I$
위의 그림을 보면 (a)는 오리지널 Observed Data이고, (b)는 PCA분석을 통해 직교 축으로 Transformation 시킨 데이터이다. 마지막으로 (c)는 이렇게 찾아준 데이터를 Scailing을 통해 규모를 맞춰준 자료이다.
이러한 변환을 통해 차후의 알고리즘을 좀 더 쉽게 돌릴 수 있다.
ICA를 돌리는 대표적인 알고리즘은 Projection Pursuit, FastICA, Infomax 등이 있다. 이 중에 가장 대표적인 Projection Pursuit만 알아보자
Projection Pursuit의 알고리즘은 간단하다.
- 전처리를 통해 형성된 벡터 축들 중 위의 기준에 따라서 가장 적합한 W축을 찾아낸다. (Kurtosis/Negentropy)
- Gram-Schmidt Process를 이용해 새로운 W축을 찾는데, 이때도 마찬가지로 기준을 최적화 하는 축을 찾는다.
- 목표로 하는 Source 개수에 도달할 때까지 반복한다.
모든 알고리즘에 공통적으로 $\textbf{y} = \textbf{w}^TZ$에 대해 목적함수를 최대치로 만드는 $\textbf{w}$를 찾고 그람-슈미트 프로세스를 이용해서 이와 직교하는 축들을 계속 찾아주는 과정이 들어 있다.
5. Scikit - Learn
사이킷런에서는 ICA에 대한 모듈을 제공하고 있다. Scikit-learn에서 사용하는 알고리즘은 FastICA이다. 아래는 그 함수에 대한 설명이다.
Parameters
- algorithm : 신호를 하나씩 추정하거나 동시에 추정한다.
- whiten : 전처리 작업 여부
- fun : Negentropy를 근사할때 사용할 근사함수의 형태 - logcosh,exp,cube 등
- fun_args : 근사함수의 인수
- w_init : mixing matrix의 초기값
- compute_sources : False 일시, Mixing matrix만 계산하고 소스 추정은 하지않음
Attributes
S = WK
- K : 전처리 전 PCA 행렬
- W : Mixing Matrix
- S : 추정 소스 행렬
지금까지 Independent Components Analysis에 대해서 알아보았다. ICA는 이론적 기반이 1980년 대부터 만들어지기 시작하여 1999년에야 널리 쓰여지기 시작한 비교적 최신 기법이다. 그래도 최신의 최신까지는 아직 먼 것 같다. 계속 공부를 해서 나중에는 정말 2010년대에 개발되고 있는 기법에 대해서도 살펴보아야 겠다.
또, NMF 때도 그랬지만 논문으로 읽으니 개략적인 개념은 이해하겠으나, 디테일한 부분에서 어떻게 되는지는 그다지 이해가 가지 않는다. 역시나 직접 구현을 해봐야 체화를 할 수 있을 것 같다. 다음에 시간이 날 때 직접 구현을 해보아야 겠다.
다음에 할 포스팅은 여러 특수한 PCA들이다. 특히 Sparce한 데이터를 어떻게 다루는 지에 대해서 자세히 공부를 해볼 것 같다.
참고문헌 - Alaa Tharwat(2018). [Independent component analysis: An introduction]