다음과 같은 모델을 가정하자
$\def \b#1{\textbf{#1}}$
$y_i = Z_i \b a_i + X_i \beta + \epsilon_i,$ $\epsilon_i \sim N(0,\kappa I)$
$\alpha_i \sim \overset{K}{\underset{k=1}{\sum}}\pi_k N(\alpha_i ; \mu_k ,\Sigma_k)$
$z_i \in R^{n_i \times q} ,a_i \in R^q , X_i \in R^{n_i \times p} , \beta \in R^p $
i = 1,2,…,N
j = 1,2,…,$n_k$
위의 notation에서 $y_i$ 부분이 기존의 선형모델과 같은 scalar 가 아니라 이미 벡터의 형태임에 주의하자. 이 모델은 Linear Mixed Effect Models에서 random effect part가 GMM을 따른다고 가정한 모델이다.
notation이 매우 햇갈리는데 데이터를 기준으로 설명하자면, 16000개의 자료 전체를 활용해서 1개의 $\beta$값이 추정되고 자료를 1500개의 Id를 기준으로 나눈 부분 자료를 이용하여 random effect $a_i$를 1500개를 추정하게 된다. 마지막으로 이 1500개에 대해서 다시 K개의 군집을 가정해서 군집분석을 진행하여 1500개의 random effect를 K로 설명해내게 된다.
이에 대한 Bayesian Sturcture를 짜보자
1. Prior 설정하기
$y_i \sim N(Z_i \b a_i + X_i \beta ,\epsilon_i)$
$\beta \sim N(0,\tau_\beta) $
$\epsilon_i \sim N(0,\kappa I)$
$\kappa \sim IG(a,b)$
$\alpha_i \sim \overset{K}{\underset{k=1}{\sum}}\pi_k N(\alpha_i ; \mu_k ,\Sigma_k)$
$\mu_k \sim N(0,\tau_\mu I)$
$\Sigma_k \sim InvWishart(\nu,D)$
$\pi \overset{K}{\sim} Diri(\Gamma)$
여기서 $a_i$가 GMM이므로 Latent Variable $c_i$를 설정해준다면 문제가 조금 더 쉽게 풀린다.
$a_{c_i} \equiv (a_i \mid c_i =k) \sim N(\alpha_i ; \mu_k , \Sigma_k)$
2. Full Conditional Distribution
위와 같은 설정하에서 찾아줘야하는 모수는 $\beta,\alpha, \kappa, c_i ,\pi, \mu ,\Sigma$이다.
이에 따라서 Full Joint Distribution을 써주자
$p(\beta,\kappa,\alpha,\mu,\Sigma \mid \b y) \propto p(\b y \mid \beta ,\kappa ,\alpha , c) p(\beta) p(\kappa) p(\alpha \mid \mu , \Sigma , c,\pi ) p(\mu) p(\Sigma) p(c \mid \pi) p(\pi)$
각 파트의 분포는 다음과 같다.
-
$p(\b y \mid \beta , \kappa ,\alpha ,c) = \prod_{i=1}^N N(y_i;Z_i \b a_i +X_i \beta , \kappa I) = (\frac{1}{2 \pi \kappa})^{\frac{N}{2}}exp(-\frac{1}{2 \kappa}\overset{N}{\underset{i=1}{\sum}}(y_i-Z_i \b a_i -X_i \beta)^T(y_i-Z_i \b a_i -X_i \beta))$
-
$p(\beta) = N(\beta; 0, \tau_\beta I) = (\frac{1}{2 \pi \tau_\beta})^{\frac{p}{2}}exp(-\frac{1}{2\tau_\beta}\beta^T\beta)$
-
$p(\kappa) = IG(\kappa ;a,b) = \frac{b^a}{\Gamma(a)}\kappa^{-a-1}exp(-\frac{b}{\kappa})$
-
$p(\alpha \mid \mu , \Sigma , \pi, c) = \prod_{i=1}^N N(a_{c_{i}};\mu_{c_i},\Sigma_{c_i}) = (\frac{1}{2 \pi })^{\frac{p}{2}}det(\Sigma_{c_i})^{-\frac{1}{2}}exp(-\frac{1}{2}(a_{c_i}-\mu_{c_i})^T\Sigma_{c_i}^{-1}(a_{c_i}-\mu_{c_i}))$
$= \prod_{i=1}^{N}\prod_{k=1}^{K}N(a_i;\mu_k,\Sigma_k)^{I(c_i=k)}$
-
$p(\mu) = \prod_k ^K N(\mu_k;0,\tau_\mu I) = (\frac{1}{2 \pi \tau_\mu})^{\frac{k}{2}}exp(-\frac{1}{2\tau_\mu}\mu^T\mu)$
-
$p(\Sigma) = \prod_k ^KInvWishart(\Sigma_k ; \nu,D)$
-
$p(c \mid \pi) = \prod_i ^N Multi(c_i ; \pi) p(c \mid \pi) = \prod_{i=1}^{N}\prod_{k=1}^{K}\pi_k^{I(c_i=k)}$
-
$p(\pi) = Diri(\Gamma)$
이들을 활용하여 Full-Conditional-Distribution을 찾아보자
편의를 위해 상위 i와 무관하게 모든 데이터를 함께 가지는 notation을 정해주자
- $D = {\bigcup_{i=1}^N Z_i,X_i,\b y_i}$
- $\b Z = { \bigcup_{i=1}^N Z_i}$
- $\b X = {\bigcup_{i=1}^N X_i }$
- $\b y = { \bigcup_{i=1}^N \b y_i }$
- $n = \sum_{i=1}^N n_i$
a. $p(\beta \mid D,\cdot) \propto exp(-\frac{1}{2 \kappa}\overset{N}{\underset{i=1}{\sum}}\overset{n_i}{\underset{j=1}{\sum}}(y_j-Z_j \b a_j -X_j\beta)^2)exp(-\frac{1}{2\tau_\beta}\beta^T\beta)$
$\sim N(\frac{1}{\kappa}(\frac{1}{\kappa}X^TX+\frac{1}{\tau_B}I)^{-1}X^T([y-Z\b a]),(\frac{1}{\kappa}X^TX+\frac{1}{\tau_B}I)^{-1})$
$[y-Z\b a] \equiv [\bigcup_{i=1}^N y_i-Z_ia_i]$
b. $p(\kappa \mid D,\cdot) \propto (\frac{1}{2 \pi \kappa})^{\frac{N}{2}}exp(-\frac{1}{2 \kappa}\overset{N}{\underset{i=1}{\sum}}\overset{n_i}{\underset{j=1}{\sum}}(y_j-Z_j \b a_j -X_j\beta)^2)\frac{1}{\kappa}^{a+1}exp(-\frac{b}{\kappa})$
$\sim IG(a+\frac{n}{2},b+\frac{1}{2}\overset{N}{\underset{i=1}{\sum}}\overset{n_i}{\underset{j=1}{\sum}}(y_j-Z_j \b a_j -X_j\beta)^2)$
아래 부분은 a가 따르는 군집에 따라서 결정된다. 따라서 $i = 1,2,…,K$에 따라서 독립적으로 이루어지므로 추정도 독립적으로 해주면 된다. 아래와 같은 notation을 사용하자
- $D_k = {\bigcup_{i=1}^N Z_i,X_i,\b y_i \mid c_i = k}$
- $\b Z_k = { \bigcup_{i=1}^N Z_i \mid c_i = k}$
- $\b X_k = {\bigcup_{i=1}^N X_i \mid c_i = k}$
- $\b y_k = { \bigcup_{i=1}^N \b y_i \mid c_i = k}$
- $n_k = \sum_{i=1}^N \sum_{j=1}^{n_i} I(c_i =k)$
c. $p(\alpha_i \mid D_k ,\cdot) \propto \prod_{j=1}^{n_i} N(y_{j};Z_{i}a_{i}+X_{i}\beta,\kappa)\prod_k N(a_{i};\mu_k,\Sigma_k)^{I(c_i=k)} $
$\propto exp(-\frac{1}{2\kappa}(y_k-Z_k\alpha_k-X_k\beta)^T(y_k-Z_k\alpha_k-X_k\beta))exp(-\frac{1}{2}(\alpha_k-\mu_k)^T\Sigma_k^{-1}(\alpha_k-\mu_k))$
$=exp(-\frac{1}{2}(\alpha_k^T(\frac{1}{\kappa}Z_k^TZ_k+\Sigma^{-1})\alpha_k-2(\frac{1}{\kappa}(\b y_k-X_k\beta)^TZ_k+\mu_k^T\Sigma_k^{-1})\alpha_k))$
$\sim N((\frac{1}{\kappa}Z_k^TZ_k+\Sigma^{-1})^{-1}(\frac{1}{\kappa}Z_k^T(y_k-X_k\beta)+\Sigma^{-1}\mu_k),(\frac{1}{\kappa}Z_k^TZ_k+\Sigma^{-1})^{-1})$
d. $p(\mu_k \mid D_k) \propto \prod_{j=1}^{n_k} N(a_{j};\mu_k,\Sigma_k) N(\mu_k ;0,\tau_\mu I)$
$\propto exp(-\frac{1}{2} \sum_j^{n_k} (a_j - \mu_k )^T \Sigma_k^{-1} (a_j-\mu_k)) exp(-\frac{1}{2\tau_\mu} \mu_k^T \mu_k)$
$= exp(-\frac{1}{2}(\mu_k^T(n_k\Sigma_k^{-1}-\frac{1}{\tau_k} I)\mu_k -2 \sum_j^{n_k} \mu_k^T\Sigma_k^{-1}a_j))$
$\sim N( (n_k \Sigma_k^{-1}+\frac{1}{\tau_\mu} I)^{-1}(\sum_j^{n_k} \Sigma_k^{-1} a_j), (n_k\Sigma_k^{-1}+\frac{1}{\tau_\mu} I)^{-1})$
wishart 분포의 경우 알려진 conjugate 성질을 그대로 사용해주었다.
e. $p(\Sigma_k \mid \cdot ) \sim Inv-Wisart(\nu+ n_k,D+\sum_{i=1}^{n_k}(a_i-\mu_k)(a_i-\mu_k)^T)$
디리클레 분포도 알려진 conjugate 성질을 그대로 사용해주었다.
f. $p(\pi \mid \cdot) \sim Diri({\gamma+n_k}_{k=1}^{K})$
g. $p(c_i \mid \cdot) \propto \prod_{k=1}^{K}N(a_i;\mu_k,\Sigma_k)^{I(c_i=k)}\prod_{k=1}^{K}\pi_k^{I(c_i=k)}$
$=\prod_{k=1}^{K}{\pi_kN(a_i;\mu_k,\Sigma_k)}^{I(c_i=k)}$
$\sim Multi({\frac{\pi_kN(a_i;\mu_k\Sigma_k)}{\sum_k\pi_kN(a_i;\mu_k\Sigma_k)}}_{k=1}^{K})$
3. Coding
우선 데이터와 필요한 패키지를 불러오자
data = read.csv("FMR_data.csv")
library("rlist")
library("MCMCpack")
library("tidyverse")
library("mvtnorm")
X = as.matrix(data[,c(6,7,8)])
Z = as.matrix(data[,c(3,4,5)])
y = as.matrix(data[,9])
다음으로, 필요한 셋팅들을 해주자
n = dim(X)[1]
N = 1500
K = 3
p=3
q=3
iter=1000
prior의 상수부들을 정의해주자
tau_beta = 1
a=1
b=1
tau_mu = 1
nu = 1
D = diag(1,3)
gamma = rep(1,K)
알고리즘의 Initial Point를 설정해주자
beta_temp =rep(1,p)
kappa_temp = 1
mu_k_temp = list()
sigma_k_temp = list()
for (k in 1:K){
mu_k_temp = list.append(mu_k_temp,c(1,1,k))
sigma_k_temp = list.append(sigma_k_temp,D)
}
pi_temp = rep(1,K)/K
ci_temp = sample(c(1:K),size=1500,replace=TRUE,prob=pi_temp)
alpha_temp = c(1,1,1)
for (i in 1:1499){
alpha_temp = rbind(alpha_temp,c(1,1,1))
}
앞선 실습들과 마찬가지로 효율을 위해 iteration에서 변하지 않는 부분들을 미리 계산해주자
xtx = t(X)%*%X
ztz = list()
for (k in 1:1500){
target = Z[data$ID==k,]
ztz = list.append(ztz,t(target)%*%target)
}
다음으로 모수 샘플들을 수집할 인스턴스를 만들어주자. $\beta$,$\kappa$,$\pi$,$c$ 같은 경우는 단일 상수라 일반적인 벡터로도 샘플을 쌓을 수 있지만, 나머지는 행렬의 형태라 좀 더 범용성 있는 자료 구조인 list를 사용해주었다.
beta_post = c(beta_temp)
kappa_post = c(kappa_temp)
alpha_post = list(alpha_temp)
mu_k_post = list(mu_k_temp)
Sigma_k_post = list(sigma_k_temp)
pi_post = c(pi_temp)
ci_post = c(ci_temp)
마지막으로 iteration part이다.
# iteration
for (it in 1:iter){
## beta
res = c()
for (i in 1:1500){
res = append(res,y[data$ID==i] - Z[data$ID==i,]%*%as.matrix(alpha_temp[i,]))
}
beta_cov = solve((xtx/kappa_temp+diag(1,3)/tau_beta))
beta_mu = beta_cov%*%t(X)%*%res/kappa_temp
beta_temp = mvrnorm(1,beta_mu,beta_cov)
## kappa
kappa_temp = rinvgamma(1,a+n/2,b + sum((res - X%*%beta_temp)^2)/2)
## alpha
alpha_temp = c()
for (i in 1:1500){
alpha_cov = solve(ztz[[i]]/kappa_temp + solve(sigma_k_temp[[ci_temp[i]]]))
alpha_mu =alpha_cov%*%(t(Z[data$ID==i,])%*%(y[data$ID==i]-X[data$ID==i,]%*%beta_temp)/kappa_temp+solve(sigma_k_temp[[ci_temp[i]]])%*%mu_k_temp[[ci_temp[i]]])
alpha_temp = rbind(alpha_temp,mvrnorm(1,alpha_mu,alpha_cov))
}
## mu_k
mu_k_temp = list()
for (k in 1:K){
nk = dim(alpha_temp[ci_temp==k,])[1]
mu_k_cov = solve(nk*solve(sigma_k_temp[[k]])+diag(1,3)/tau_mu)
mu_k_mu = mu_k_cov%*%solve(sigma_k_temp[[k]])%*%t(rep(1,dim(alpha_temp[ci_temp==k,])[1])%*%alpha_temp[ci_temp==k,])
mu_k_temp = list.append(mu_k_temp,mvrnorm(1,mu_k_mu,mu_k_cov))
}
## Sigma_k
sigma_k_temp = list()
for (k in 1:K){
nk = dim(alpha_temp[ci_temp==k,])[1]
sigma_k_nu = nu+dim(alpha_temp[ci_temp==k,])[1]
sigma_k_D_sum=0
for (m in 1:nk){
sigma_k_D_sum_m = as.matrix(alpha_temp[ci_temp == k,][m,]-mu_k_temp[[k]])%*%t(alpha_temp[ci_temp == k,][m,]-mu_k_temp[[k]])
sigma_k_D_sum = sigma_k_D_sum + sigma_k_D_sum_m
}
sigma_k_D = D+sigma_k_D_sum
sigma_k_temp = list.append(sigma_k_temp,riwish(sigma_k_nu,sigma_k_D))
}
## pi
Gamma = c()
for (k in 1:K){
Gamma = append(Gamma,dim(alpha_temp[ci_temp==k,])[1])
}
pi_temp = rdirichlet(1,gamma + Gamma)
## Latent Variable C
ci_temp = c()
for (i in 1:1500){
density = c()
for (k in 1:K) {
density = append(density,dmvnorm(alpha_temp[i,],mu_k_temp[[k]],sigma_k_temp[[k]],log=TRUE)+log(pi_temp[k]))
}
ci_temp = append(ci_temp,sample(c(1:K),1,prob=exp(density-max(density))))
}
beta_post = rbind(beta_post,beta_temp)
kappa_post = c(kappa_post,kappa_temp)
alpha_post = list.append(alpha_post,alpha_temp)
mu_k_post = list.append(mu_k_post,mu_k_temp)
Sigma_k_post = list.append(Sigma_k_post,sigma_k_temp)
pi_post = rbind(pi_post,pi_temp)
ci_post = rbind(ci_post,ci_temp)
sse = c()
for (i in 1:1500){
sse = append(sse,(y[data$ID==i] - Z[data$ID==i,]%*%as.matrix(alpha_temp[i,])-X[data$ID==i,]%*%beta_temp)^2)
}
print(paste(it,"번째 R2: ",(1-sum(sse)/var(y)/dim(y)[1])*100,"%"))
ci_score = c()
for (i in 1:1500){
ci_score = c(ci_score,(ci_post[it,i])!=ci_post[it-1,i])
}
print(paste(it,"번째 군집 변동율: ",sum(ci_score)/15,"%"))
}
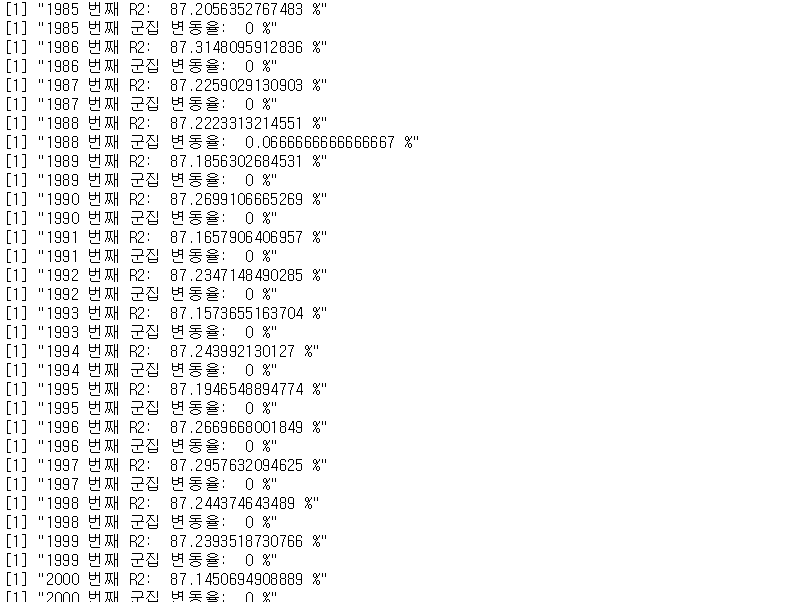
Iteration의 끝 부분에 진행상황을 체크하기 위해서 $R^2$와 군집의 변동 상태를 확인해주는 코드를 넣어주었다. 구조상 군집화가 완료되면 군집의 변동이 거의 일어나지 않으므로 수렴의 형태로 접어들게 될것이다.
아래는 그 진행 결과이다. 시간관계상 2000번의 샘플링만을 사용해 주었다.
4.결과물 확인
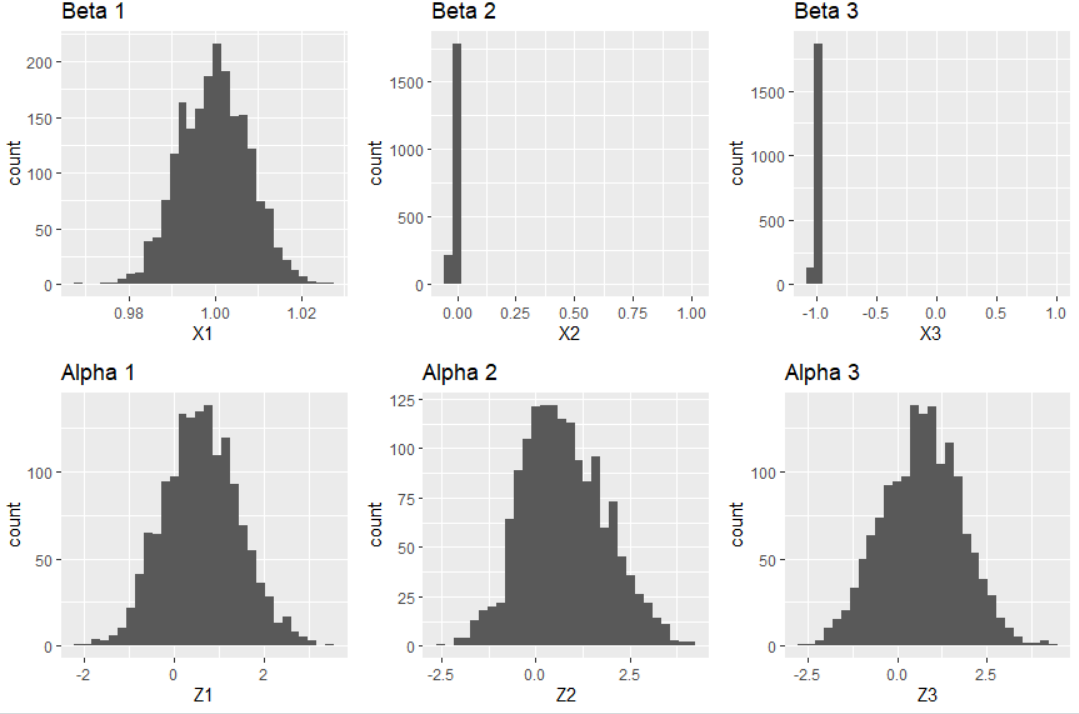
우선 각 계수 샘플들의 히스토그램은 다음과 같다.
p1 <- data.frame(beta_post) %>%
ggplot(aes(x=X1)) +geom_histogram()+ggtitle("Beta 1")
p2 <- data.frame(beta_post) %>%
ggplot(aes(x=X2)) +geom_histogram()+ggtitle("Beta 2")
p3 <- data.frame(beta_post) %>%
ggplot(aes(x=X3)) +geom_histogram()+ggtitle("Beta 3")
p4 <- data.frame(alpha_post) %>%
ggplot(aes(x=Z1)) +geom_histogram()+ggtitle("Alpha 1")
p5 <- data.frame(alpha_post) %>%
ggplot(aes(x=Z2)) +geom_histogram()+ggtitle("Alpha 2")
p6 <- data.frame(alpha_post) %>%
ggplot(aes(x=Z3)) +geom_histogram()+ggtitle("Alpha 3")
grid.arrange(p1,p2,p3,p4,p5,p6,nrow=2)
군집들의 평균들은 다음과 같다.
| Z1 | Z2 | Z3 | |
|---|---|---|---|
| 군집1 | 0.0027 | 2.4868 | -2.2747 |
| 군집2 | -0.4922 | -0.0123 | 0.4896 |
| 군집3 | 0.9818 | -0.9589 | 0.0239 |
마지막으로 alpha의 기울기에 대한 군집분석 그림을 그려주자
result = data.frame(cbind("a1"=alpha_temp[,1],"a2"=alpha_temp[,2],"a3"=alpha_temp[,3],"label"=ci_temp))
p1 <- ggplot(result, aes(x=a2,y=a1, fill=label, color=label)) +
geom_point()
p2 <- ggplot(result, aes(x=a3,y=a1, fill=label, color=label)) +
geom_point()
p3 <- ggplot(result, aes(x=a2,y=a3, fill=label, color=label)) +
geom_point()
grid.arrange(p1,p2,ncol=2)