0. 개요
Matrix Factorization은 행렬을 주요 요인으로 분해한다는 개념으로, 천문학,화학,자연어 처리, 사운드 분석, 추천 시스템 등에서 다양하게 응용되는 개념이라고 한다.
앞서 포스팅한 PCA나 군집분석과는 다르게, 이번에는 좀 더 일반화된 개념부터 접근해서 행렬 분해의 전반을 공부 해보려고 한다.
현재까지 예정되어 있는 학습 내용은 다음과 같다.
- Bregman Divergence
- Generalized Non Negative Matrix Factorizaion with Bregamnn Divergence
- Independent Component Analysis
- Incremental PCA, Kernel PCA, Sparse PCA
- Factorization Model
1. Bregman Divergence 란?
Bregman Divergence은 통계학과 Information Theory에서 주로 사용하는 개념으로, 거리의 일반화 개념이다.
그 정의는 다음과 같다.
$D_{F}(p,q) = F(p)-F(q)-<\nabla F(q), p-q>$
where $F:\Omega \rightarrow R$ is continuously-differentiable and convex function defined on a closed convex set $\Omega$
<>는 에르미트 내적
이는 q에서의 1차 테일러 근사를 통한 근사 F’(p)값과 실제 F(p)값의 차이로 해석 될 수 있다.
좀 더 구체적으로 설명하기 위해 아래그림을 보자
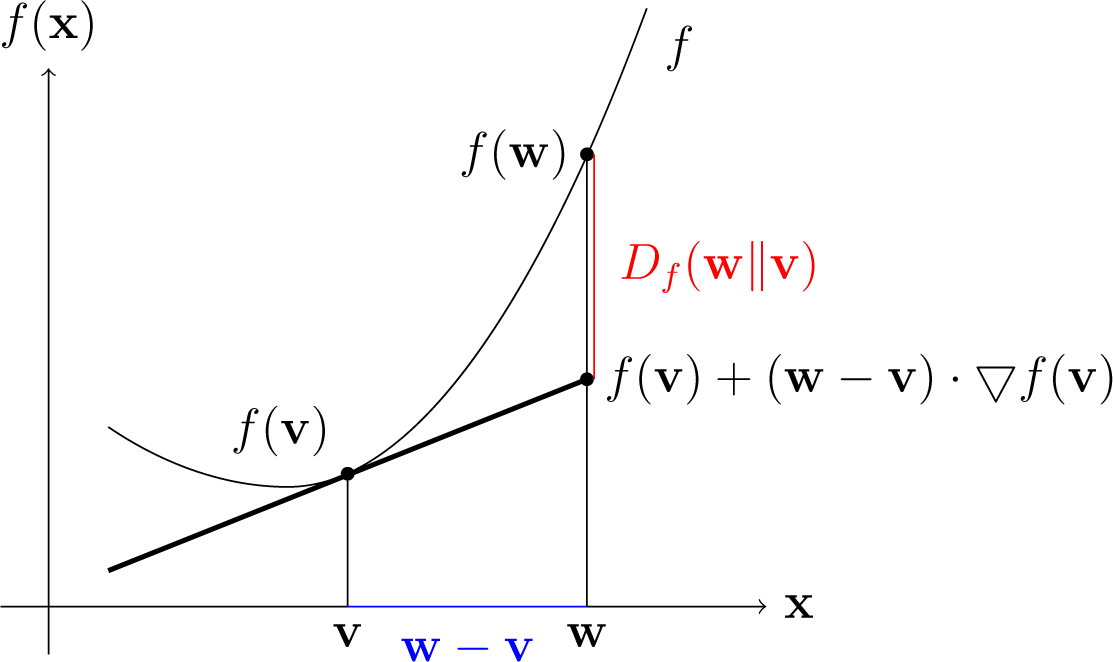
여기서 $F’(p) = F(q)-\nabla F(q)(q-p) = F(q)+ \nabla F(q)(p-q)$이므로 실제값과의 차이가 Bregmann Divergence가 된다.
Bregman Divergence는 수학에서 정의하는 metric의 symmetric과 triangle inequality 공리들을 만족하지 못하는 거리척도이다. 그러나 Optimization 계열의 알고리즘에서 매우 핵심적으로 쓰이는 척도이며 점 p가 통계적 분포로 해석될시 Statistical Distance로 연결이 된다고 하므로 중요도가 매우 높다.
Bregman Divergence 는 다음과 같은 성질을 가지고 있다.
- Non-Negativity
- Convexity - $D_{F}(p,q)$는 p에 대해서 convexity가 성립한다. (q로는 성립하지 않을 수 있음)
- Linearity
- $D_{F_1+\lambda F_2}(p,q) = D_{F_1}(p,q) + \lambda D_{F2}(p,q)$
- 주목할 점은 p나 q에 대해서가 아니라 거리척도인 함수 그 자체에 대해서 선형성이 성립한다는 점이다.
- Bregman Divergence의 p가 Random Vector일 때, 이를 최소화 시키는 q는 Random Vector의 Mean Vector이다.
또, 아래와 같은 이유로 Metric의 공리를 만족하지 못한다.
- Asymmetric - $D_F(p,q) \neq D_F (q,p)$
- Triangle Inequality를 만족하지 못한다 - {triangle Inequality : $f(q_1) +f(p,q_2) > f(q_1+q_2)$}
2. 적용 예시
a. $F(\textbf{x}) = ||\textbf{x}||^2 = \textbf{x}^t\textbf{x}$ (Euclidean Norm)일 경우
- $D_F(p,q) = \mid \mid p-q \mid \mid^2$ (;Euclidean Distance) 이다.
유도)
$\nabla F(\textbf{x}) = \frac{\delta}{\delta \textbf{x}}\textbf{x}^t\textbf{x} = 2\textbf{x}$
$D_F(p,q) = F(p)-F(q)-<\nabla F(q),p-q>$
$=p^tp-q^tq-2q^t(p-q)$
$=p^tp-2q^tp+q^tq = (p-q)^t(p-q)$
$= \mid \mid p-q \mid \mid ^2$
b. $F(\textbf{x}) = \frac{1}{2}\textbf{x}^tQ\textbf{x}$의 경우
- $D_F(p,q) = \frac{1}{2}(p-q)^tQ(p-q)$ (;Mahalanobis Distance)
유도)
$\nabla F(\textbf{x}) = \frac{\delta}{\delta \textbf{x}}\frac{1}{2}\textbf{x}^tQ\textbf{x} = Q\textbf{x}$
$D_F(p,q) = F(p)-F(q)-<\nabla F(q),p-q>$
$= \frac{1}{2}p^tQp-\frac{1}{2}q^tQq-(p-q)^tQ\textbf{q}$
$=\frac{1}{2}p^tQp-p^tQq+\frac{1}{2}q^tQq$
$=\frac{1}{2}(p-q)^tQ(p-q)$
Mahalanobis 거리는 유클리드 거리의 일반화로써 사용가능하며 통계학에서 적용될 시 Covariance , Correlation으로도 적용가능하다. 또, 점 p와 분포 D 사이의 거리를 정의하는 척도로도 사용할 수 있다고 한다.
c.$F(p)=\int p(x) \ log \ p(x) \delta x$ (;entropy)의 경우
- $D_F(p,q) = \int p(x) \ log \frac{p(x)}{q(x)} \delta x - \int p(x) \delta x + \int q(x) \delta x$
$=KL(P \mid \mid Q)$ (; Kullback-Leibler Divergence)
유도)
$\nabla F(p)$는 functional derivate 이므로 다음 공식을 통해 유도를 해내자
$\int \frac{\delta F}{\delta p(x)} \eta(x) d x=[\frac{d}{d \epsilon}F(p+\epsilon\eta]_{\epsilon \rightarrow 0}$
$=[\frac{d}{d \epsilon} \int (p+\epsilon \eta)log(p+\epsilon \eta)dx]_{\epsilon \rightarrow 0} $
$= [\frac{d}{d \epsilon}\int p \ log(p+\epsilon \eta)dx+\frac{d}{d \epsilon}\int \epsilon \eta log(p+\epsilon \eta)dx]_{\epsilon \rightarrow 0}$
$=[\int \frac{p\eta}{p+\epsilon\eta}dx+\int \eta log(p+\epsilon\eta)dx+\int \frac{\epsilon \eta^2}{p+\eta \epsilon} dx]_{\epsilon \rightarrow 0}$
$=[\int (1+log(p+\epsilon \eta))\eta(x) dx]_{\epsilon \rightarrow 0}$
$=\int (1+log \ p) \eta(x) dx$
$\therefore \nabla F(p) = 1+log \ p $
$D_F(p,q) = F(p)-F(q)-<\nabla F(q),p-q >$
$=\int p \ log \ p \ d x-\int q \ log \ q \ d x -<1+log \ q ,(p-q)> $
$= \int p \ log \ p \ dx - \int \ q \ log \ q \ dx - \int(1+log \ q )(p-q) dx$
$= \int p \ log \frac{p}{q} dx -\int p(x) dx + \int q(x) dx$
이때, p(x)와 q(x)가 확률밀도 함수라면 아래와 같이 간소화 된다.
$= \int p(x) \ log \frac{p(x)}{q(x)} dx$
Kullback - Leibler Divergence $KL(P \mid \mid Q)$는 다음과 같이 해석될 수 있다.
- P 대신 Q를 사용했을 때의 정보 획득량 (Information Gain) (in Machine Learning)
- Q에 대한 P의 상대적 엔트로피 (Relative Entropy) (in Information Theory)
- 사전분포 Q에서 사후분포 P로 업데이트 되었을때의 정보 획득량 (in Bayesian Statistics)
- P의 근사분포로 Q를 사용했을 때의 정보 소실량 (in Bayesian Variational Inference)
d.$F(p) = - \underset{i}{\sum}log \ p(i)$ (Negative Logarithmic Function)
- $D_{F}(p,q) = \underset{i}{\sum}(\frac{p(i)}{q(i)}-log \frac{p(i)}{q(i)}-1)$ (Itakura-Saito Distance)
유도)
$F(p)$ 역시 함수를 인풋으로 받는 Fucntional 이다. 따라서 위와 같이 풀어주자
$\sum_i \nabla F \eta = [\frac{d}{d \epsilon}F(p+\epsilon \eta)]_{\epsilon \rightarrow 0}$
$=[\frac{d}{d \epsilon} (-\sum_i log (p(i)+ \epsilon \eta(i))]_{\epsilon \rightarrow 0}$
$= [-\sum_i \frac{\eta(i)}{p(i)+\epsilon \eta(i)}]_{\epsilon \rightarrow 0}$
$= \sum_i (-\frac{1}{p(i)})\eta$
$\therefore \nabla F = -\frac{1}{p(i)}$
$D_F = F(p) - F(q) -<\nabla F(q),p-q>$
$= -\sum log \ p(i) + \sum log \ q(i) + \sum\frac{p(i)-q(i)}{q(i)}$
$= \sum_i (\frac{p(i)}{q(i)} -log \frac{p(i)}{q(i)}-1)$
- Itakura - Saito Distence는 Exponential Family를 따르는 두 집단간의 비교를 하는 것에 쓰일 수 있다고 한다.
- 또 Non-Negative Matrix Factoriazation을 할 때의 척도로도 사용할 수 있다고 한다.
지금까지 Bregman Divergence를 살펴보았다. Bregman Divergence는 분산, 유클리드 거리, KL로 응용이 될 수 있는 범용성 높은 거리정의이다. 특히 통계학에서 매우 중요한 개념이므로 한번 살펴보는 것은 필수불가분하다.
다음 포스팅에서는 이 Bregman Divergence가 행렬분해에 어떻게 적용되는 지에 대해 살펴 볼 것이다.
출처 - https://en.wikipedia.org/wiki/Bregman_divergence
