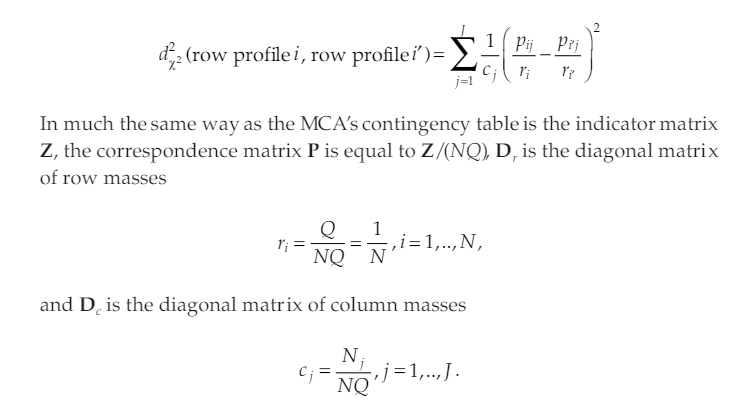1. 차원 축소란?
- 기술적 처리를 수월케하고 수학적 난점을 해결하기 위해 데이터를 압축하는 것
- 정보 손실을 최소화 하면서 데이터의 크기를 줄이는 것이 목표
- 빅데이터 시대에 필수적인 기술이 되어가고 있음
a. 빅데이터의 문제점
-
오버피팅
- 피쳐의 수가 과하게 많아져서 Bias가 줄어드는 것 이상으로 Var가 커지는 현상
-
추정대상의 증가
- 샘플 개수는 그대로 인데 피쳐수가 늘어난다면 그만큼 개별 피쳐 관련 모수의 추정 신뢰도가 낮아진다. (자유도의 문제)
-
N « P의 문제
-
샘플의 개수가 피쳐의 수보다 훨씬 적은 경우 회귀분석이 불가능 하다.
ex) 정밀공정을 가진 첨단 제품의 불량율 분석
우주선 발사의 실패 요인 분석
-
-
차원의 저주
- 차원이 늘어감에 따라 발생하는 여러 부정적인 현상의 총칭
- 사실 위의 문제들을 모두 포함하는 말일 수 있음
- 모든 샘플들이 아웃라이어화가 되어 전형성이 사라짐
- 데이터가 비어있거나 없는 것들이 늘어나 sparce 데이터를 만들어 낼 수 있음
- 차원이 늘어감에 따라 발생하는 여러 부정적인 현상의 총칭
b. 차원 축소의 기본적인 전략
- 불필요한(redundunt) 변수는 지워버리고 중요한 변수를 남기자
- 변수선택, 군집분석, 변수 추출 등의 방법을 사용
- 변수추출 - 기존의 변수들을 이용해 새로운 변수를 추출해내는 것
2. 차원 축소 기법
a. Factorization 모델
-
데이터 프레임: 데이터가 직사각형 모양의 행렬 꼴로 저장되어 있는 데이터 저장 양식
- 행렬을 도입할 수 있다는 것에서 무수히 많은 수학적 기법을 사용할 수 있으므로 DS영역에서는 사실상 표준으로 자리 잡아있다.
- 행은 개별 관측 개체가 가진 어떠한 속성들의 묶음으로 이루어져 있고 열(피쳐)은 어떠한 속성에 대해 관측 개체들이 가진 값들의 묶음으로 이루어져 있다.
-
Factor: 여러 피쳐들 속에서 대표성을 띌 수 있는 잠재적 요인을 의미한다.
ex) 과자 들의 식감, 향, 맛, 가격, 무게, 디자인, 광고 모델 등의 속성이 저장된 데이터 프레임이 있을 때, 가격, 무게는 상품의 규격으로, 디자인, 광고 모델은 상품의 외관으로, 식감, 향, 맛 등은 상품의 맛 이라는 요인으로 간략화 될 수 있다.
-
Factorization은 이러한 잠재적인 요인들을 뽑아낸후 행렬분해를 통해 데이터 프레임을 새로운 두가지 행렬로 표현하는 것을 의미한다.
-
잠재적인 요인을 뽑아내는 방법으로는 Principal Components 기법과 Maximum Likelihood 기법 등 여러가지 방법이 있으며 최근에는 딥 러닝을 기반으로 하여 뽑아내는 것이 연구 되고 있다.
b. PCA(;Principal Components Analysis)
PCA에 대한 설명 이전에 변수 추출의 방법 중 하나인 SLC라는 것의 이해가 필요하다.
SLC(;Standard Linear Conbination)
오직 선형조합만을 이용해 새로운 변수를 만들어 내는것
$z=\delta^tx\delta^t\delta=1$ where $delta^t\delta=1$
이때 어떠한 변수의 분산이 크다면 변수의 정보량이 많은 것으로 인식될 수 있다.
그런데 Var과 관련하여 다음과 같은 수식이 만족된다.
max(Var(z))=max($\delta^t \Sigma \delta$) = $\lambda_1$ (;$\lambda_1 $은 $\Sigma$의 아이젠 밸류 중 가장 큰 값)
이는 라그랑주 승수법이나 쿼드래딕 폼의 최대값 공식을 활용해서 증명이 가능하며 이때의 delta는 고유벡터가 된다.
따라서 데이터 프레임의 공분산 행렬을 Spectral Decomposition한 후 그 고유값과 고유벡터를 활용하여 행렬 분해를 실시하면 선형적으로 가장 정보량을 많이 담고 있는 축($\delta_1$)과 그 축에 직교하여 선형적 정보를 공유하지 않는 축($\delta_2,\delta_3,…$)으로 factor를 찾아낼 수 있다. 이렇게 만들어진 직교 하는 Factor들을 행렬의 PC(;Principal Components)라고 하며 이러한 PC들을 찾아내는 것을 PCA(;PC Analysis)라고 한다. 이때 고유값들은 고유벡터의 정보량 (Var(z))와 일치하므로 고유값들이 작은 Factor 순 부터 제거를 해나감으로써 정보량 손실을 최소화 하면서 데이터 프레임의 크기를 줄일 수 있다.
**PCA의 특징은 다음과 같다. **
- 스케일링에 민감하다.
- 분산=정보량으로 보고 있으므로 분산을 표준화하여 공분산 단위를 일치시켜 줘야 한다.
- 연속형 자료에서만 사용가능하다.
- 공분산 행렬에 분해를 시행하는 것이므로 당연한 일이다.
- 축들의 이름이 사라진다.
- 따라서 직접 해석이 불가하며 요인분석을 통해서 간접 해석을 해야한다.
- 비지도 학습이다.
- 결과물과 타깃변수의 관계를 반영하지 않는다.
c. MCA(; Multiple Correspondence Analysis)
PCA에서는 변수간의 관계성이 공분산으로 표현된다. 즉, 변수간의 관계가 밀접할 수록 공분산이 커지며 PCA는 이를 포착하여 정보량이 많은 변수를 새로이 만들어낸다.
그러나 이러한 방식은 범주형에서는 사용이 불가능 하다. 범주형 변수, 예를 들어 동물의 종과 눈 색깔 간에는 공분산이라는 것이 정의될 수 없기 때문이다.
그래서 나올 수 있는 아이디어가 바로 범주형 변수의 관계성 지표로 쓰일 수 있는 두 변수의 독립성 검정에 대한 카이제곱 검정통계량이다. 카이제곱 검정통계량도 공분산과 마찬가지로 두 변수의 관계성이 커질수록 커지는 지표이다.
변수 간의 카이제곱 검정 통계량으로 행렬을 만든 다음 거기에 대해 Spectral Decomposition을 하여서 Factor를 찾아내는 것이 바로 CA(;Correspondec Analysis)이다. MCA는 이러한 CA를 여러변수로 확장시킨 것이다.
CA를 통해서 만들어진 요인들을 이용하면 범주형 변수를 연속형 변수로 임베딩 할 수 있다. CA의 결과물은 흔히 2차원의 좌표계아래 명목 범주들이 패턴을 띄면서 퍼져있는 형태인다.
아래는 MCA에 관한 문헌을 찾아 읽고 그 컨셉을 확인 내용이다. (참조-The Visualization and Verbalization of Data)
MCA를 하기 위해서는 아래와 같이 범주별 원핫 인코딩을 한 것과 같은 행렬을 만든다. 이를 Indicator Matrix 혹은 Complete Disjuctive Matrix라고 부른다.
이렇게 만들어진 행렬 X를 다음과 같이 변환하면 $\chi^2$ 행렬이 만들어진다.
$D_r^{-\frac{1}{2}}(Z/N-\textbf{r}\textbf{c}^T)D_c^{-1\frac{1}{2}} = \Gamma\Lambda\Delta$
나머지는 PCA와 같은 방식을 취하면 된다. 또한 이 경우 개체별로의 거리를 다음과 같이 정의된다.
그 결과, 범주형 자료간의 거리를 카이제곱 통계량을 기반으로 좌표평면에서 정의할 수 있게 되었다. 수치형 자료의 좌표평면에서 자료들을 제어 할 수 있게 되었기 때문에 범주형 변수들에 PCA와 유사한 방법론을 적용해서 차원축소를 해줄 수 있는 것이다.
3. Factor Analysis
요인분석은 위와 같이 PCA나 MCA를 통해서 구해낸 팩터들과 기존의 변수들의 관계성을 분석함으로써 요인을 해석하는 것을 의미한다.
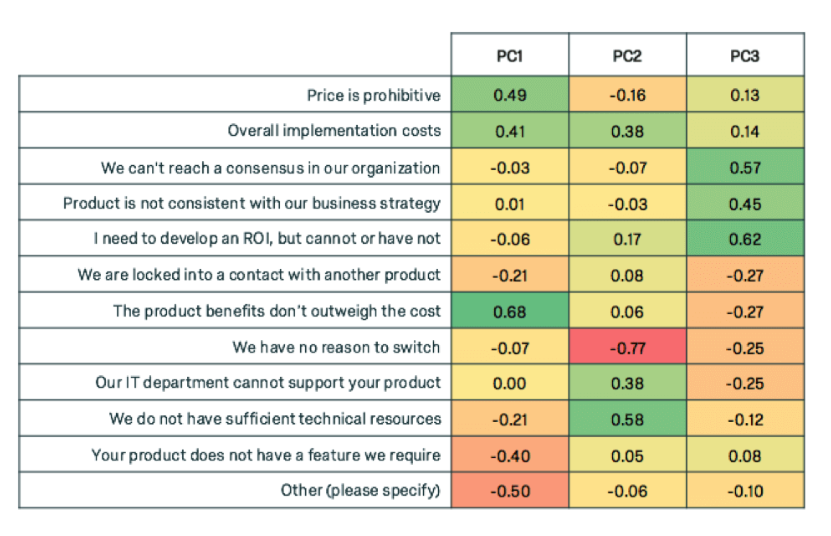
일반적으로 연속형 변수에서 뽑아낸 요인들의 경우, 요인과 기존 변수간의 상관계수를 체크함으로써 가능하다. PCA의 경우 이 상관계수 행렬을 PC Loading이라고 부른다. 그 예시는 아래와 같다.
위에서 첫번째 변수와 밀접하게 연관있는것은 모두 금액과 관련한 것이다. 따라서 PC1은 금액에 관한 변수라고 해석 할 수 있다.
지금까지 전통적으로 쓰이던 차원축소의 방법에 대해서 정리해보았다. 그러나 최근에는 딥러닝의 임베딩 레이어를 활용하여 팩터를 뽑아내는 방식을 사용할 수 있다고 한다. 따라서 다음에 기회가 닿는다면 딥러닝을 통해서 차원축소를 하는 방식에 대해서 탐구를 해 봐야겠다.