image

Dimensionality Reduction

1. 군집분석이란?

  • 유사도(Similarity)와 상이도($\approx$ Distance)를 기준으로 데이터를 그룹핑하는 것
  • 비지도 학습의 일종 - Y 없이 데이터의 패턴을 인식하여 군집화를 이뤄냄
  • 정답지가 없는 만큼 분석가가 정답이 되어야한다. 따라서 군집분석의 모든 과정을 체화하고 그에 따른 결과물을 해석해낼 필요가 있다.

A. 목적

  • EDA를 위해서
  • 다른 분석을 위한 전처리로써
  • 기타 등등 (고객 분류 등)

B. 거리 (Distance)의 정의

  • Interval Variable의 경우

    • 일반적으로 민코스키 거리 계열을 사용한다.
\[d(X_i,X_j)=(\sum_{k=1}^{n}|X_{ik}-X_{jk}|^r)^{1/r}\]

이때 r=$\infty$일시 Chebyshev Distance, r=1일시 Manhattan Distance, r=2 일시 우리가 잘 알고 있는 Euclid Distance라고 부른다.

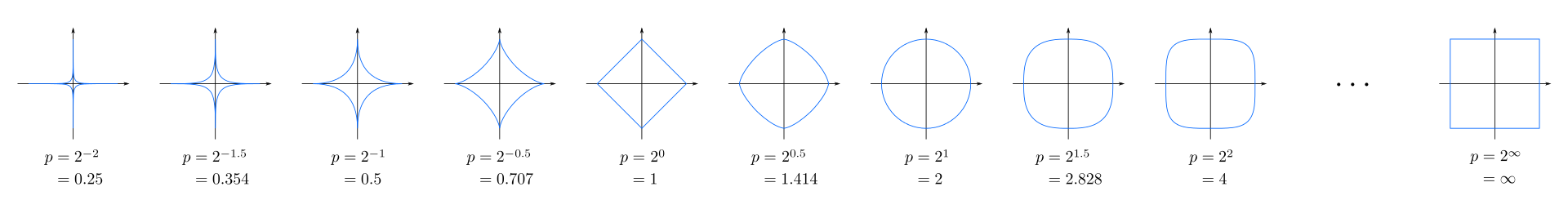
figure1

  • Categorical Variable의 경우

    • MCA 포스팅에서 보았듯이 카이제곱 검정통계량으로 거리표현을 할 수 있지만 군집분석에서는 일반적으로 아래와 같은 방식을 사용한다.

      • $d(X_i,X_j) = \frac{r+s}{q+r+s+t}$ (; Simple Matching Coefficients)

      • $d(X_i,X_j) = \frac{r+s}{q+r+s}$ (; Jaccard Coefficients)

$x_i \backslash x_j$ 1 0
1 q r
0 s t

위의 표는 범주형 변수를 이항변수화 하여 두 자료의 일치율을 거리화 한 것이다.

일반적으로 이항변수화를 할때는 다수파를 0으로, 소수파를 1로 코딩하는 데 이 경우 분할표에서 t가 차지하는 비율이 너무 커져 거리계산에 영향을 크게 미칠 수 있다. 따라서 t를 계산에서 제하는 방식이 자카드 계수이다.

2. 군집분석의 알고리즘

A. 분할기법

  • 임의의 점을 중심점(;Centroid)로 삼은 다음 이를 일정한 알고리즘하에 자료를 가장 잘 대표하는 점으로 최적화 시키는 방식이다.
  • K-Means(평균,연속형 자료), K-Modes(최빈값,범주형 자료) , K-prototype(평균과 최빈값, 혼합형 자료), K-Medoids(중위값, 연속형 자료) 등의 알고리즘이 있다.

K-Means Algorithm

  • k-means 알고리즘은 가장 간단하게 적용할 수 있는 기법이다.

  • 알고리즘

    1. 임의의 센트로이드로 임의의 클러스터를 구축

    2. 클러스터링 된 객체들의 평균을 새로운 센트로이드로 설정
    3. 2번의 센트로이드를 기준으로 다시 클러스터를 구축
    4. 2~3번 반복
  • 장점
    • 확장성(;Scalabilty)이 좋아 빅데이터에도 사용하기 쉽다.
    • 계산량이 적다
    • 이해하기 용이하다 - 센트로이드의 값이 곧 군집의 대표값이다.
  • 단점
    • 군집의 개수를 미리 설정해줘야 한다. (하이퍼 파라미터)
    • 군집의 크기와 모양이 경직 되어 있다.
      • 센트로이드를 중심으로 하는 특징상 항상 원형으로 군집이 짜여지며, 각 군집의 크기가 거의 유사해짐
    • 아웃라이어에 취약하다.
      • 평균을 지표로 쓰는 만큼 아웃라이어에 취약하다

예시 1. 아이리스 데이터

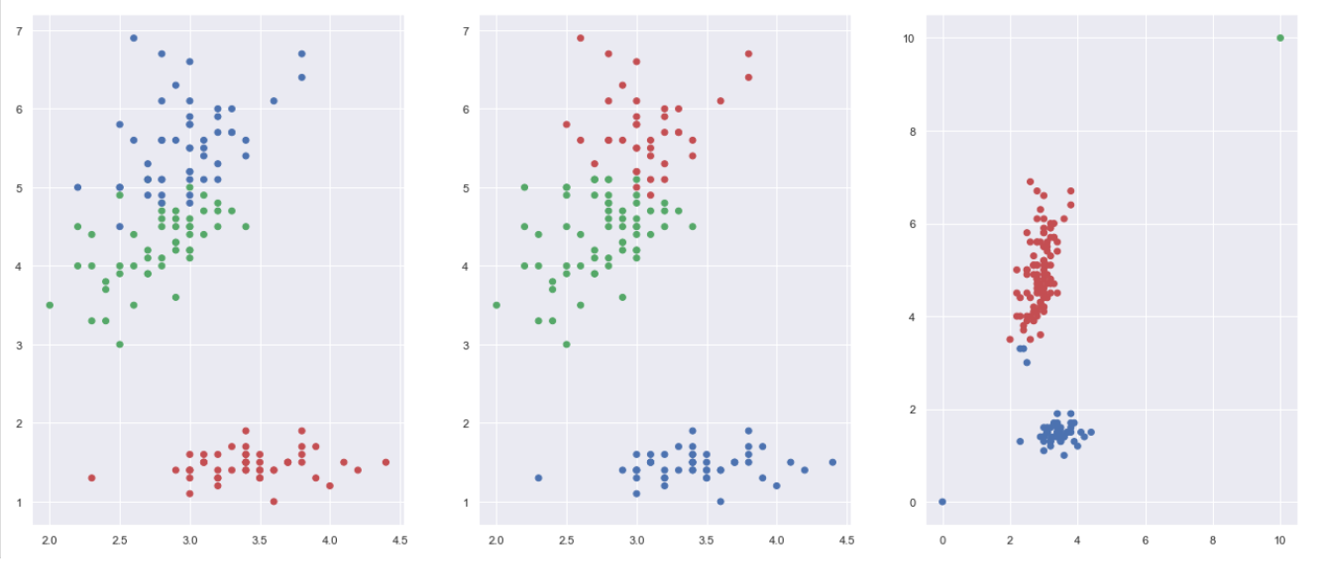
figure1

  • 첫번째 그림은 품종별로 채색이 된 아이리스 자료(True 값)이며 두번째 그림은 품종정보없이 군집분석으로 나눈 결과물(Predict 값)이다.
  • 첫번째와 두번째의 군집분포에 거의 차이가 없으므로 k-means의 성능을 알 수 있다.
  • 세번째 그림은 똑같은 아이리스 데이터에 아웃라이어를 추가해낸 것인데, 아웃라이어가 끼어있으므로 k-mean의 성능이 극단적으로 낮아짐을 알 수 있다.

예시 2. 사이킷런의 샘플 데이터

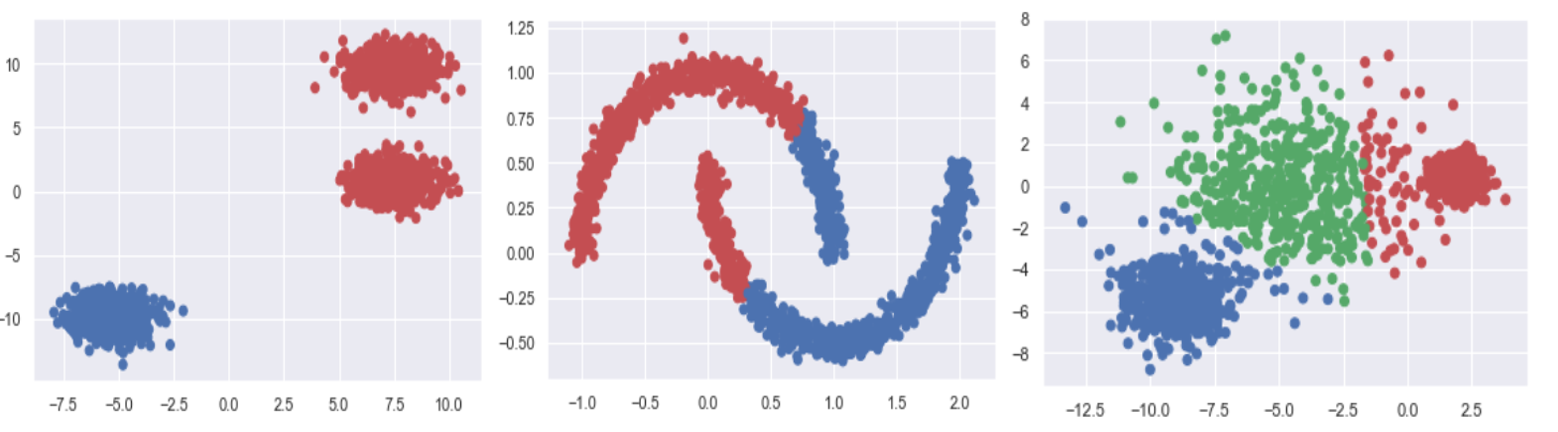
figure1

  • 첫번째 그림은 하이퍼 파라미터를 잘 못 설정해 줬을때 군집분석 성능이 떨어짐을 보여준다.
  • 두번째 그림은 k-means가 원형이 아닌 군집의 모양을 찾아줄 수 없음을 보여준다.
  • 세번째 그림은 k-means가 군집 간의 크기를 달리 해줄 수 없음을 보여준다.

B. 계층 기법

  • 단순한 방식으로 클러스터를 만든 뒤 이를 거리기준으로 합치거나 나누어가면서 목표로 하는 개수만큼의 군집을 만들어나가는 방법이다.

DIANA(;Divisive ANAlysis) (분할적 계층 군집화 기법)

  • 하나의 군집을 만든 다음 일정한 기준하에 이를 잘게 쪼개어 나가면서 목표한 개수만큼의 군집을 만들어 내는 방식이다.

AGNES (;AGglomerative NESting, 집괴적 계층 군집화 기법)

  • 분할기법을 통해 임의의 군집을 수십~수백개 만든 뒤, 군집끼리 거리를 측정하여 서로 가까운 순으로 합쳐나가는 방법이다. DIANA보다는 AGNES가 좀 더 일반적인 방법이다.

  • 알고리즘
    1. 임의의 클러스터들을 형성 (k-means 기반)
    2. 각 클러스터의 거리를 비교하여 가장 가까운 클러스터들 순으로 합쳐나감
    3. 목표 클러스터 개수를 달성 시 스탑

  • 특징

    • 군집의 모양과 크기가 매우 유연하다.
    • 확장성이 낮아 계산량이 많다.
    • 아웃라이어를 다루기 힘들다.
    • 거리의 정의가 하이퍼파라미터 이므로 튜닝이 힘들다.
    • 응용기법이 많아 단점이 어느정도 보완되어 있다.

  • AGNES의 하이퍼 파라미터

    • 클러스터의 개수 (k-means와 동일)

    • Distance(linkage) (괄호 안은 sk-learn에서의 용어)

      • Minimum Distance(Single)

        ​ $d_{min}(C_i,C_j)=min_{p \in C_i, p’ \in C_j}d(p,p’)$

      • Maximum Distance(Complete)

        ​ $d_{max}(C_i,C_j)=max_{p \in C_i, p’ \in C_j}d(p,p’)$

      • Average Distance (Average)

        $d_{avg}(C_i,C_j)=\frac{1}{n_in_j}\sum_{p \in C_i} \sum_{p’ \in C_j}d(p,p’)$

      • SSW(Ward)

        ​ $d_{ward}(C_i,C_j)=\frac{1}{n_k}\sum_{i=1}^{n_k} d(p_i,m_k) $

        • $n_k$는 두 군집을 합쳤을 때의 총 개수, $m_k$는 두군집을 합쳤을때의 센트로이드

예시 . 사이킷 런의 샘플 데이터

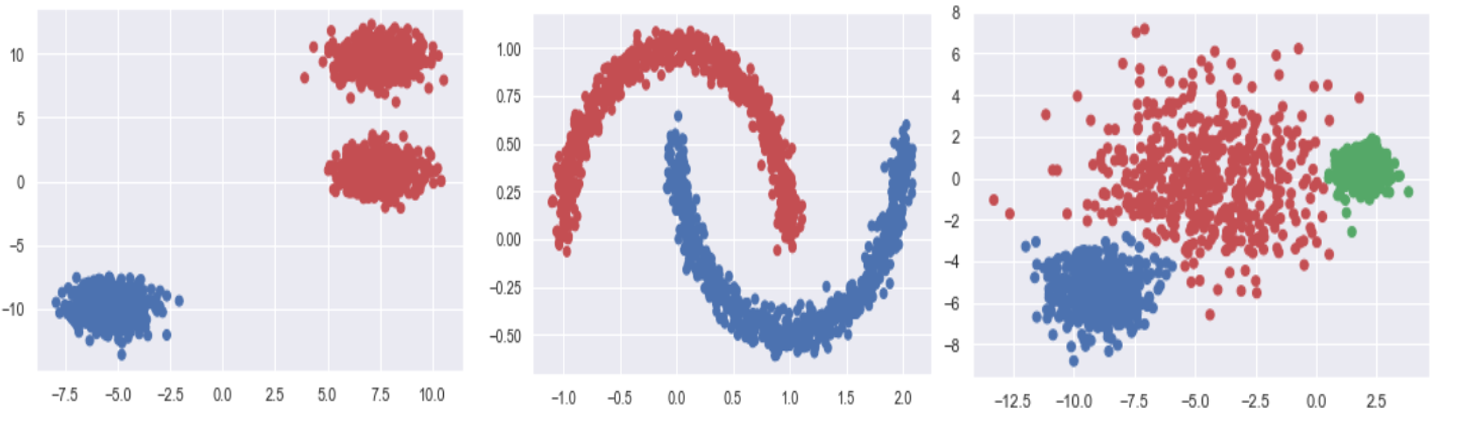
figure1

  • 첫번째 그림은 AGNES도 여전히 군집개수를 잘 설정해줘야 함을 보여준다.
  • 두번째 그림은 k-means와는 다르게 AGNES가 비구형의 군집을 잘 포착해낼 수 있음을 보여준다.
  • 세번째 그림은 AGNES에서는 군집들의 크기가 유사하다는 제약이 없다는 것을 보여준다.

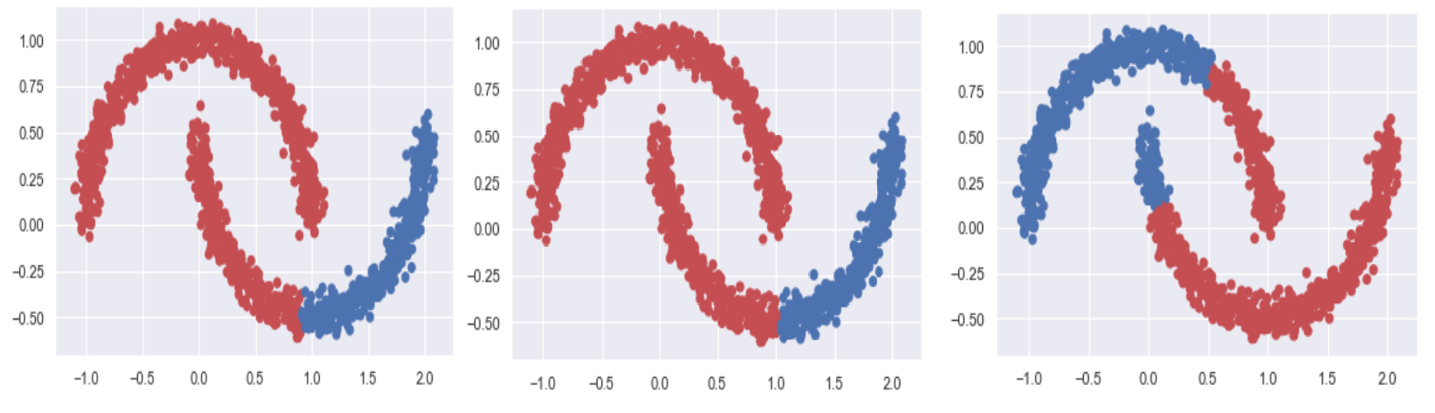
figure1

  • 세 그림은 각각 ward, average, max를 기준으로 한 군집분석결과물이다.
  • 하이퍼파라미터 설정에 따라서 결과물이 천차만별로 나올 수 있음을 보여준다.

계층기법의 응용기법

  • Birch 기법
    • 하부 클러스터들의 모든 객체를 저장하는 것이 아니라, 0차,1차,2차 적률을 저장하여 계산량을 극도로 줄인 것
  • CURE 기법(Clustering Using REpresentatives)
    • 연속형 자료에서만 사용할 수 있음
    • 하부 클러스터들의 모든 객체를 저장하는 것이 아니라, 임의로 샘플링된 객체들을 대푯값으로 삼아 거리를 평가하는 기법
  • ROCK 기법
    • 범주형 자료에서만 사용할 수 있음
    • 상호 연결성을 지표로 쓰는 네트워크 적인 기법
  • Chameleon 기법
    • Cure와 Rock기법을 혼합한 기법
    • 혼합형 자료에서 사용가능
    • knn 그래프를 기반으로 쓰기에 계산량이 매우 많음

C. 밀도 기법

DBSCAN(Density Based Spatial Clustering Application with Noise)

  • 객체의 이웃을 직접 찾아서 군집을 형성하는 기법

  • 알고리즘

    1. 어느 점을 기준으로 반경 x내에 점이 n개 이상 있으면 하나의 군집으로 인식하고 그점은 Core Point라고 부름
    2. 반경내에 점을 만족하지 않을 경우 다른 군집의 경계점이 되고 스스로 군집형성은 하지않음
    3. 어느 Core Point가 다른 군집의 일부가 될 때 두 군집을 서로 합침
    4. 어느 군집에도 속하지 않는 다면 아웃라이어로 취급함

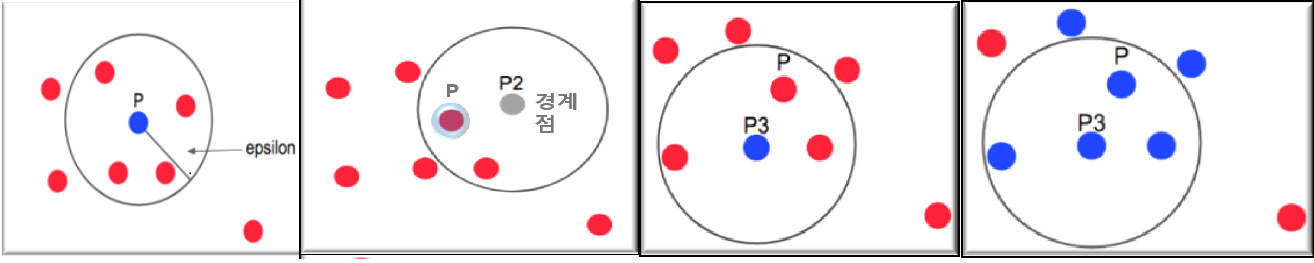
image-20200224172552150

  • DBSCAN의 특징
    • 클러스터 개수를 설정해줄 필요가 없음
    • 유연성이 뛰어나고 아웃라이어를 다루기 쉬움
    • 하이퍼 파라미터 튜닝이 아주 어려움(eps=원의 반경,n_samples=군집 간주 최소 객체 수)

figure13

  • 하이퍼 파라미터 튜닝 문제를 해결하기 위해 eps를 자동 할당해주는 OPTICS라는 응용기법이 있음

3. 군집분석의 주요 이슈

  • 유연성 - 군집분석의 결과물이 모양과 크기가 유연한가?

  • 이상치 견고성 - 이상치에 견고한가?

  • 확장성 - 큰 자료/ 복잡한 자료에 사용할 수 있는가?

  • 계산량 - 컴퓨팅이 효율적으로 이뤄지는가?

  • 하이퍼 파라미터 - 하이퍼 파라미터에 얼마나, 어떻게 영향을 받는가?

  • 접근성- 군집에 대해 얼마나 직관적인 이해를 할 수 있는가?

You May Also Enjoy