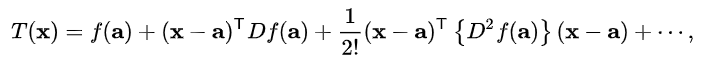Linear Operator in Euclidean Space
Matrix는 데이터 사이언스의 거의 모든 영역에서 사용되는 매우 중요한 수학적 개념이다.
그런데 데이터사이언스의 많은 영역들은 학부수준의 선형대수학만 가지고도 충분하지만 조금만 깊게 들어가도 힐버트 공간 이론, 실해석학, 함수 해석학을 알고 있어야 하는 개념들이 나오게 된다.
따라서 이 포스팅을 통해 이러한 행렬의 고급 개념들을 정리해보고자 한다.
순서는 다음과 같다.
- Analytic meaning of Matrix
- Basic concepts in operator
- Quadratic form
- Function and operator
최소한의 증명은 적을 것이지만 넘어가도 좋을것 같다.
1. Analytic Meaning of Operator
정의
행렬은 해석학적으로 정의하면 a Linear Operator defined on Euclidean Vector Space라고 볼 수 있다.
이 단어를 하나하나 해석해보자.
- Vector Space: 어떠한 집합이 덧셈(addition)과 스칼라곱(scalar multiplication)에 닫혀있을때 이 집합을 vector space라고 부른다.
- 집합 A가 연산 k에 닫혀있다는 의미는 A 내부의 어느 원소에 대해 k연산을 시행해도 이 값이 여전히 집합 A 내부에 있음을 의미한다
- Euclidean Space: 실수들의 k개 순서쌍(i.e. k-tuple)으로 이루어진 vector space에 다음의 inner product, norm, metric이 정의되었을때 Euclidean space라고 말한다.
- $1. \left< x,y\right> = \sum x_iy_i, 2.\parallel x \parallel = \sqrt{\left< x,x \right>},3. d(x,y) = \parallel x-y \parallel$
- Operator는 mapping(function)과 동일한 의미로 해석하면 된다.
- Linear Operator: 어떠한 operator f가 모든 원소 x,y, 스칼라 a,b에 대해 $f(a x + b y)=af(x)+bf(y)$가 성립할때 linear operator라고 말한다.
즉, matrix는 유클리드 공간에서 성립하는 linear operator를 이르는 말이다. 역으로, 유클리드 공간에서 정의되는 모든 Linear operator는 행렬의 형태로 표현할 수 있다.
즉, 행렬이 아닌 linear operator on euclidean space는 존재하지 않으며 linear operator가 아닌 행렬은 존재하지 않는다.
pf) $\def\inn#1{\left<#1\right>}$
Let A be an operator on $\mathbb{R}^n$ and let ${e_1,e_2,…e_n}$ be a standard basis of $\mathbb{R}^n$.
Define $a_{ij} = \inn{Ae_j,e_i}$
Then, for any vector $x = \sum \xi_j e_j$, $\inn{x,e_i}=\xi_i$ which means ith value of vector x is $\xi$
$Ax = \sum \xi_j A e_j$ (by linearity of A)
Then, $\inn{Ax,e_i} = \inn{\sum \xi_j A e_j,e_i} = \sum \xi_j \inn{A e_j ,e_i} = \sum a_{ij} \xi_j$
That is, the result of any linear operator become product sum between element of vector and elements of 2-dimensional box-shape array i.e. matrix. $\square$
이 증명에서는 내적이 구체적으로 정의되지 않음에 유의하자. 즉, 내적이 바뀌어도 linear operator는 행렬 꼴이다.
추가적으로 위 증명은 basis가 특정되고 $Ax$가 bounded하다면 모든 힐버트 공간에서 사용할 수 있다. 즉 무한개의 basis를 가지는 함수공간 내에서도 bounded linear operator를 무한개의 원소를 가지는 행렬로써 표현할 수 있긴 하다.
이 포스팅에서 다루는 공간은 후반까지 유클리드 공간으로 제한되어 있으므로 이후로는 operator를 matrix와 동의어로 사용할 것이다.
행렬의 종류와 내적
기초 선형대수학에서는 symmetric이나 idempotent 같은 행렬이 가질 수 있는 여러가지 성질을 배울 수 있다.
그런데 이 개념들은 matrix의 모양에 따라서 얻을 수 있는 일종의 관측결과이지 수학적인 역할에서 온 의미는 아니다. 좀 더 어원의 근원을 살펴보면 이러한 성질들은 내적과의 상호작용에 따라서 얻어진 명칭임을 알 수 있다. 따라서 우선은 내적의 정의부터 살펴보자.
- Standard Inner Product on Complex Space.
- 위에서 정한 내적에 대해, 복소 공간에서는 내적이 약간 다르게 정의된다.
- $\inn{x,y} = \sum x_i \bar{y_i}$ where $\bar{y_i} = a - bi $ (conjugate complex number) for $y_i=a+bi ,\qquad a,b \in \mathbb{R} $
- 이러한 정의에 맞춰서 스칼라 곱의 경우 $\inn{x,ay}=\bar{a}\inn{x,y}$로 표현된다.
- 실수 공간에서만 사용할 경우 $x =\bar{x}$이므로 일반성을 잃지 않고 위의 정의를 사용할 수 있다.
내적을 이렇게 정의한 후 각 행렬들의 개념에 대해서 살펴보자.
- Operator Norm
- Operator A의 Norm은 다음과 같이 정의된다. $\parallel A\parallel = \underset{\parallel x \parallel=1}{\sup} \mid \inn{Ax,x}\mid$
- 이는 나중에 살펴볼테지만 A의 Quadratic Form이 가질 수 있는 최댓값이며 First Eigen Value와 같다.
- Adjoint Operator
- $A$가 힐버트 공간 $H$의 bounded operator일시 다음을 만족하는 operator $A^\ast$는 $A$의 adjoint operator라고 부른다. $\inn{Ax,y} = \inn{x,A^\ast y} \mbox{ where } \forall x,y \in H$
- 실수 공간에서 내적이 정의되면 $\inn {Ax,y} = x^tA^ty = x^t A^{\ast}y = \inn{x,A^{\ast}y} $ for all x,y 이므로 $A^t = A^{\ast}$가 된다. 복소수 공간에서는 ${a_{ij}^{\ast}}= {\bar{a_{ji}}}$이다.
- 즉 transpose의 복소수 확장판으로 보면 된다.
- $\parallel A\parallel = \parallel A^{\ast} \parallel$가 성립한다.
- Self-Adjoint Operator (Hermitian)
- $A = A^{\ast}$일시, A를 self-adjoint matrix라고 부른다.
- 실수에서는 $A=A^t$ 이므로 symmetric으로 생각할 수 있다. 즉 symmetric의 복소수 확장판이다.
- 어떤 operator T에 대해서 $T^{\ast} T,T+T^{\ast}$는 self-adjoint matrix이다.
-
Invertible Operator
- 어떤 operator A에 대해 A의 치역에서 정의된 어떤 operator B가 $\forall x \in R(A),ABx=x$ and $\forall x\in D(A) ,BAx=x$ 를 만족시 A를 invertible하다고 하며 B를 A의 inverse operator라고 부른다.
- A가 invertible하지 않을 경우 inverse operator의 일반화 버전인 $ABAx=Ax$를 만족하는 g-inverse B가 존재한다.
- Inverse Operator에 대해서는 나중에 자세히 이야기 하자.
-
Positive Operator
- 어떤 self-adjoint operator A에 대해 $\inn{Ax,x} \geq 0 \quad \forall x \in H$ 일시 A를 positive operator라고 부른다.
- 추가적으로, A가 유클리드 공간의 operator일시 $\inn{Ax,x} \geq 0$인 경우에 Positive semi-definite 혹은 non-negative definite라고 부르며 $\inn{Ax,x}>0$인 경우에 positive definite라고 부른다.
- Normal Operator
- 어떤 operator A가 A의 adjoint matrix와 commutes할때, 즉 $AA^{\ast}=A^{\ast}A$일때 A를 normal operator라고 부른다.
- A bounded operator is normal if and only if $\parallel Tx \parallel = \parallel T^{\ast} x \parallel , \quad \forall x \in H$
- 위의 $\parallel T\parallel = \parallel T^{\ast} \parallel$는 어떤 경우에도 성립하지만 이는 $\parallel x \parallel =1$에서의 최대값일때의 등호를 이야기 함에 주의하자. 즉, $\parallel Tx \parallel = \parallel T^{\ast} x \parallel, \quad \forall x \in H$가 더 강한 조건이다.
- If T is normal operator, then $\parallel T^n \parallel = \parallel T \parallel^n$
-
Isometric operator
- 힐버트 공간 H 위의 어떤 operator T에 대해 $\parallel Tx \parallel = \parallel x \parallel, \quad \forall x \in H$일시 T를 isometric operator라고 부른다.
- A bounded operator T on Hilbert space H is isometric if and only if $T^\ast T = I$ on H
- Isometric은 인풋의 길이를 보존하는 operator임을 주목하자.
-
Compact Operator
- 어떤 operator A의 range가 compact set일때 A를 compact operator라고 부른다. 이는 completely continuous operator라고도 불린다.
- Compact Operator는 물론 bounded operator이다.
-
Hilbert-Schmidt Theorem
- For every compact, self-adjoint operator A on an infinite-dimensional Hilbert spcae H, there exists an orthonormal system of eigenvectors correpsonding to nonzero eigen values that every element $x \in H$ has a unique representation in the form $x = \sum_{n=1}^{\infty} \alpha_n \mu_n + \nu$ where $\alpha_n \in \mathbb{C}$ and $\nu \in N(A)$
2. Concepts handled with operator
Eigen value
Eigen vector와 Eigen value는 어떠한 operator A에 대해 $Av=\lambda v$가 성립하는 벡터 $v$와 스칼라 $\lambda$를 일컷는 말이다.
$Av = \lambda v$는 일종의 현상이라고 할 수 있다.
이 현상은 어떤 벡터 v를 linear transformation(Av)을 해도 강도($\lambda$)만 변하고 방향(v)은 변하지 않는 현상이기 때문이다. 따라서 이는 A라는 operator가 변화시키는 방향에 대한 정보를 제공해준다.
Determinant
Determinant란 operator에 대한 정보를 제공해주는 스칼라 값으로 여러가지 수학적 방식으로 정의될 수 있는 개념이다.
그러나 determinant라는 이름에서 알 수 있듯, determinant의 가장 핵심이 되는 역할은 operator A가 invertible한지 아닌지에 대한 정보를 제공해주는 것에 있다. Determinant가 0일시 역행렬은 존재하지 않는다.
Determinant는 열벡터들이 이루는 초-평행사변형의 부피값이라고 해석할 수 있다. 이 평행사변형의 한 축의 길이라도 0일시 부피값은 0이 되며, 역행렬은 존재하지 않는다.
Determinant는 열벡터가 이루는 부피값이기 때문에 transformation된 measure의 스케일링 값이 되기도 한다. 이것이 치환적분에서 jacobian이라고 불리는 개념으로 연결된다.
$Det(A) = \prod\lambda_i$ 가 성립한다. 이를 해석하면, A의 eigen value 중 하나라도 0이라면 역행렬이 존재하지 않는다고 해석할 수 있으며 아이젠 밸류의 곱이 초 평행사변형의 부피값이라는 것은 아이젠 밸류와 벡터가 초 평행사변형에서 어떠한 부분에 있는지를 짐작할 수 있게 해준다.
Decomposition
모든 행렬은 가장 기초가 되는 세 종류의 행렬로 분해가 될 수 있다. 즉 다음과 같다.
$A = \prod_{k=1}^{n_k} \prod_{j=1}^{n_j} \prod_{i=1}^{n_i} T_{1i} T_{2j} T_{3k}$
$Type1: {Te_1,…,Te_k}$ is a permutation of ${e_1,e_2,…e_k}$ (Exchanging matrix)
$Type2 : Te_1 = \alpha e_1, T e_i=e_i$ (Scaling matrix)
$Type3: Te_1 = e_1+e_2, Te_i=e_i$ (Summation matrix)
ex) $T_1 =\left[ \begin{array}{cccc} 0 & 1&0&0\\ 1&0&0&0&\\ 0&0&1&0 \\ 0&0&0&1 \end{array} \right]\(,T_2=\left[ \begin{array}{cccc} \alpha & 0&0&0\\\ 0&1&0&0&\\\ 0&0&1&0 \\\ 0&0&0&1 \end{array} \right]\),T_3=\left[ \begin{array}{cccc} 1 & 0&0&0\\ 1&1&0&0&\\ 0&0&1&0 \\ 0&0&0&1 \end{array}\right]$
이들을 잘 이용하면, 행렬의 원소 하나하나를 특정할 수 있게 된다.
이러한 분해는 이들 자체로는 큰 의미는 없지만 모든 행렬이 더 작은 행렬로 분해될 수 있음을 확증시켜준다.
행렬의 분해 중 유용하게 사용되는 분해로는 다음이 있다.
- QR decomposition
- A=QR where Q is an orthonormal matrix and R is an upper triangular matrix
- 아직까지 어디에 썻다는 것은 본 적이 없다..
- Cholesky decomposition
- $A=LL^{\ast}$ where L is a lower triangular matrix and A ia a positive definite matrix.
- cholesky decomposition은 linear equation을 수치적으로 풀 때 유용한 분해이다.
- Spectral decomposition
- $A=\Gamma \Lambda \Gamma^{\ast}$ where $\Gamma$ is an orthogonal matrix, $\Lambda$ is a diagonal matrix whose entry is eigen value of A and A is self-adjoint matrix
- spectral decomposition의 유용성은 아래의 내용에 지속적으로 등장할 것이다.
- 모든 종류의 operator에 대해 spectral decomposition의 일반화 된 버전인 singular value decomposition $A = \Gamma \Lambda \Delta^{\ast} $가 존재한다.
3. Quadratic Form
정의
- Quadratic form은 operator A에 대해서 $\Phi_A (x) = \inn{Ax,x}$의 꼴을 의미한다. 유클리드 공간의 standard norm에서는 $\Phi_{A}(x) = x^t A x$이다.
- 앞서서 정의한 positive definite 개념들은 quadradic form의 sign과 연관이 있는 개념들이다.
- Self-adjoint하지 않은 operator A의 경우 $x^tAx = x^tA^{\ast}x = \frac{1}{2}x^t(A+A^{\ast})x$가 성립하므로 Operator A와 correspond 한 self-adjoint operator와 동선에 놓고 계산할 수 있다.
Operator Norm
-
Operator A의 norm 은 $\parallel A \parallel =\underset{}{\sup} \inn{Ax,x}$
-
유클리드 공간의 operator는 항상 bounded operator이므로 $\Phi_{A}(x) \leq A \parallel x\parallel$인 scalar A가 존재한다.
-
여기에 대해 $\parallel x \parallel=1 $이라는 제약을 줬을때 $\Phi_{A}(X)$가 가질 수 있는 최대값이 operator A의 norm $\parallel A\parallel$으로 정의된다.
Quadradic Form Theorem
- $\underset{x \in H}{\max} \frac{x^t Ax}{x^tBx} = \lambda_1 , \underset{x \in H}{\min} \frac{x^t Ax}{x^tBx} = \lambda_p $ where $\lambda_1$ is a maximum of eigen value of $B^{-1}A$ and $\lambda_p$ is a minimum of eigen value of $B^{-1}A$
- 이는 모든 B, x에 대해 속하며, 일반성을 잃지 않고 $\parallel x\parallel =1$이라는 제약을 둘 수 있다. 이를 이용하면 $\underset{\parallel x \parallel = 1}{\max} x^t Ax = \lambda_1$이 성립한다.
- 이를 이용하면 $\parallel A \parallel_{op} = \lambda_1 $을 얻을 수 있다.
Relation between Matrix
- Positive definite matrix는 $A>0$과 같이 표현하기도 한다. 이를 이용하면 다음이 만족할시 $x^t(A-B)x \geq 0$ 일시 $A-B >0$를 정의할 수 있으며 $A> B$ 를 이야기 할수 있다.
- 단 이 relation은 additivity,multiplicativity, transitivity가 성립하지 않는 불완전한 관계임을 유의하자.
- 위의 quadradic form theorem을 활용하면 $\lambda_p I\leq A \leq \lambda_1 I$으로 A라는 operator의 범위를 표현할 수 있다.
4. Function and Operator
Multivariate Taylor Series
- 테일러 시리즈는 무한번 미분 가능한 함수를 다항함수로 근사시켜 분석해주는 강력한 해석적 도구이다. 일반적으로는 단변량에서 다루지만 다변량에서도 테일러 근사는 존재하며 다음과 같이 정의된다.
-
이 꼴은 지나치게 복잡하므로 다변량에서의 테일러 시리즈는 다음과 같이 이차항까지만 근사해서 표현한다.
- $Df(a) = \frac{\delta f(x)}{\delta x} \mid_{x=a}$ ($Df(a) \in R^{p}$)이며 $D^2f(a) = \frac{\delta^2 f(x)}{\delta x^2} (D^2f(a) \in R^{p \times p})$이다.
- 일차항 부분은 내적이며 이차항 부분은 quadradic form임을 주목하자. 즉, 다변량에서의 테일러 시리즈는 내적과 quadradic form을 이용해서 표현된다.
Convex Function
-
Convex function은 다음과 같이 정의된다.
$f:A \rightarrow N$ is convex function if $\forall \alpha \in (0,1),\forall x,y \in A, f(ax+(1-a)y) \leq af(x)+(1-a)f(y)$
- convex 함수는 한번 미분 가능할시 $f(y) \geq f(x) + \nabla f(x)^T(y-x)$ 라는 부등식이 성립한다
- convex 함수는 두번 미분이 가능할시 $\nabla^2f \geq 0 $이라는 특징을 가진다. 즉, Hessian matrix가 positive semi - definite하다.
Function onto operator
-
operator에 대한 함수는 해석적으로 다음과 같이 정의될 수 있다.
$f(A) = \sum f(\lambda_i) \gamma_i \gamma_i^t$
-
이는 테일러 시리즈와 singular value decomposition을 응용한 결과이다.
테일러 시리즈 : $f(x) = \sum_p \frac{f^{(p)}(0)}{p!}x^p$, Spectral decomposition: $A^p = \Gamma \Lambda^p \Gamma^t = \sum \lambda_i^p \gamma_i \gamma_i^t$
$f(A) = \sum_p \frac{f^{(p)}(0)}{p!}A^p = \sum_p \frac{f^{(p)}(0)}{p!}\sum_i \lambda_i^p \gamma_i \gamma_i^t = \sum _i [\sum_p \frac{f^{(p)}(0)}{p!} \lambda_i^p] \gamma_i \gamma_i^t =\sum_i f(\lambda_i) \gamma_i \gamma_i^t$
- 예컨데 $e^{A} = \sum e^{\lambda_i} \gamma_i \gamma_i^t$로써 정의되며 양자컴퓨터의 유니터리 매트릭스를 표현하는데 사용할 수 있다.
추가적으로 projection matrix와 hilbert 공간으로의 확장까지 다룰 예정이었지만, 이까지만 해도 너어무 많아서 이들은 생략하기로 했다.
다음에 기회가 있을때 정리해보도록 하자.