[RCA] Ch1.Abstract Integration (1/2)

1. Abstract Integration

0. 들어가기에 앞서

우리는 고등학교 때부터 미적분을 공부해왔다. 미분과 적분은 현실계에서 적용 가능한 매우 훌륭한 수학적 개념이다. 미분은 변화율을 의미하며 적분은 이러한 변화의 누적분을 의미한다. 따라서 미적분은 이러한 컨셉을 응용할 수 있는 실생활의 모든 경우에 대해서 적용할 수 있다.

예를들어 물리학에서 어떤 물건의 위치를 표시한 함수의 미분값은 그 물건의 속도를 표현할 수 있고 반대로 속도 함수를 적분한 값은 그 물건의 최종 위치를 표현해준다.

그런데 적분에는 하나 더 훌륭한 성질이 존재한다. 정의역과 공역이 어떻게 되는 함수던 간에 함수가 가지는 값을 숫자 하나로 요약해주는 연산이라는 것이다. 수학적으로 표기하면 적분은 다음과 같은 함수이다.

$\int : {f} \rightarrow R$

숫자 하나로 요약해주는 것의 장점은 단순하다. 우리의 머리는 제한되어 있기 때문에 복잡한 정보를 받아들이기 힘들어 하기 때문이다. 아무리 복잡한 형태의 함수라도 숫자 하나로 요약되면 너무나도 깔끔하게 이해를 할 수 있다.

예를 들어 (0,1)의 구간에서만 값을 가지는 두 함수 f,g를 생각해보자. f가 큰가? g가 큰가?. “크다”라는 말을 하기 위해서 우리는 기준이 필요함을 알아차리게 된다. 두 함수의 최대값을 기준으로 하면 f가 더 커보인다. x=1에서의 값을 기준으로 하면 g함수가 더 커보인다. 그런데 우리는 여기서 하나의 기준을 더 가질 수 있다. 두 함수의 차이 (f-g)의 적분값을 기준으로 0보다 클시 f가, 0보다 적을시 g가 크다고 생각할 수 있다.

세가지 기준 모두 경우에 경우에 따라서 유용하게 사용할 수 있지만, 특히 마지막 적분값을 기준으로 하면 우리는 유용한 정리들을 매우 많이 얻어낼 수 있다. 특히, 힐버트 공간에서는 함수공간의 내적으로 이러한 적분을 이용한다. 이에 대해서는 나중에 다시 보기로 하자.

그런데 이렇게 적분함수를 기준으로 삼으려고 보니 몇가지 제한점들이 눈에 띈다.

• 대상이 되는 함수 f가 그 자체로 1차원 실수를 공역으로 가져야 한다

적분은 다른 공역을 허용하지 않는다. 즉 대상이 되는 함수는 다음과 같아야 한다. $f: A \rightarrow R$

다행히도, 우리는 실생활에서 대부분 이러한 함수만 관심에 두고 있으며, 더욱이 공역이 실수가 아닐시 다른 함수와 합성시켜서 공역을 실수로 만들 수 있다. 이러한 함수를 특별히 Functional 혹은 범함수라고 부른다.

• 어떠한 함수는 리만적분이 불가능할 수 있다.

리만 적분은 우리가 고등학교 때 배운 구분구적법을 의미한다. 고등학교 때 배웠을지 모르겠지만, 어떤 함수들은 이런 구분구적법이 불가능할 수 있다. 예를 들어 입력값이 무리수 일때 1을, 유리수 일때 0을 반환하는 디리클레함수를 생각할 수 있다.

그런데 이 경우, 두 함수의 비교가 불가능할것 같진 않다. 논리적으로 디리클레 함수와 $f(x)=1$인 함수를 비교하면 f 함수가 더 크기 때문이다.

따라서 어떤 함수가 적분이 불가능하다는 것은 리만적분의 정의상으로 불가능한 것이지 실제로 불가능하지는 않을 수도 있다는 의미이다. 이러한 상황 속에서 수학자들은 리만 적분으로 정의 가능한 함수의 적분보다 더 넓은 범위의 함수까지 적분이 가능한 새로운 적분의 정의를 개발해야만 했다. 이것이 바로 르벡 적분이며, Abstract Integration이 다루는 범위이다.

그러나 르벡 적분을 이해하는 것은 간단하지 않다. 르벡적분을 정의하기 위해 필요한 개념이 너무 많기 때문이다. 따라서 1장의 경우, 이러한 컨셉을 하나하나 이해한 후 최종적으로 르벡적분과 그 성질을 이해하는 것을 목표로 하고 있다. 다음이 1장에서 다루는 내용은 플로우이다 .

A. Space and Measurability

B. Simple Function

C. Measure

D. Lebesgue Integration

E. Set of Measure Zero

이 개념들은 단순히 르벡 적분을 정의하는 것을 넘어 통계학의 본질에도 연결되는 중요한 개념이다. 따라서 하나하나 제대로 숙지를 할 필요가 있다.

A. Space and Measurability

topological space와 measurable space

Space라 함은 매우 추상적인 개념이긴 하지만 직관적으로는 Set에 어떠한 성질이 추가된 것이라고 이해할 수 있다. 예를 들어 Real Space는 $(R, +,\cdot, <)$로 표기되기도 하며, R이라는 집합에 $+,\cdot,<$의 개념이 추가된 것으로 이해할 수 있다. 수학에서는 이러한 가장 기본적인 공간을 정의함으로써 연역적으로 개념을 확장해 나간다.

1장에서 사용하는 컨셉들의 배경이 되는 공간은 Topological Space와 Measurable Space 두 가지가 있다. 아래는 그 중 Topological Space의 정의이다.

Topological Space

• Topology $\tau$ in X : A collection of subset of X that satisfies following property
  • $\phi , X \in \tau$
  • For $V_i \in \tau$, $\cap_i V_i \in \tau$ (for only countable and finite $i$)
  • For $V_\alpha \in \tau$,$\cup_\alpha V_\alpha \in \tau$ (for any $\alpha$ e.g. finite, infinite, countable, uncountable)

• Topological Space : A space X that have topology $\tau$

• Open Set : Members of Topology
• Continuous Function:
  • For topological space M,N, any open set V in N and mapping $f:M\rightarrow N$,the function f is called continous if $f^{-1}(V)$ is open set for every $V \subset N$

Topology라 함은 어떤 공간 X에서 만들 수 있는 부분집합들의 집합이며 위의 정의에 맞춰서 자의적으로 정할 수 있다. 공간 X에 대해 어떠한 방식이든 자의적으로 topology를 정하게 되면 그 공간 X를 이제 topological space라고 부르겠다는 것이 전체적인 흐름이다.

갑자기 너무 많은 새로운 개념이 등장해서 당황할 수도 있지만 다 이해할 필요는 없다. 그저 기초해석학에 등장하는 Open Set과 Continuous Function이 위상수학에서 이해되는 방식이며 해당 내용 자체는 추가적으로 공부할 필요는 없다. 그러나 정말 중요한 공간은 Measurable Space이다.

Measurable Space

• $\sigma$ - algebra $M$ in X : A collection of subset of X that satisfies following property
  • $X \in M$
  • If $A$ in $M$, then $A^c$ in $M$
  • For $V_\alpha \in M$,$\cup_\alpha V_\alpha \in M$ (for countable $\alpha$ )

• Measurable Space : A space X that have $\sigma$ - algebra $M$

• Measurable Set : Members of $\sigma$ - algebra
• Measurable Function:
  • For measurable space M and topological space N, any open set V in N and mapping $f:M\rightarrow N$,the function f is called measurable if $f^{-1}(V)$ is measurable set for every $V \subset N$

위에서 등장한 topological space와 매우 유사하지만 이번에 적용되는 부분집합의 집합에 대한 성질이 바뀐 것이다. measurable function의 정의 또한 미묘하게 다른 것에 주의하자.

$\sigma$ -algebra와 Borel Sets

$\sigma$ - algebra라는 것을 굳이 새로 정하는 이유에 대해서는 차후에 simple function의 도입을 위해서 이다. 따라서 필요성과 성질에 대해서는 simple function을 다시 보면서 이해하기로 하고 일단은 받아들이도록 하자.

$ \sigma $ - algebra는 위와 같이 해당 개념이 지녀야 하는 성질을 통해서 정의된다. 이를 공리적 정의( axiomatic definition)라고 부르며 실제로는 조금 더 많은 성질을 가진다. 아래가 공리에 더해 $ \sigma$ - algebra가 추가적으로 가지는 성질이다. 증명들은 매우 간단하니 직접 해보자.

Property of $\sigma$ - algebra

1. $\phi \in M$
   • $X\in M$ 이므로 $X^c = \phi \in M$.
2. For $V_i \in M$, $\cup_{i=1}^n V_i \in M$ { Axiom can be applied to finite too }
   • By setting $V_i = \phi$ for i = n+1,n+2,….
3. For $V_{\alpha} \in M$, $\cap_\alpha V_\alpha \in M$ {for countable $\alpha$}
   • For $V_{\alpha} \in M$, $V_{\alpha}^c$ is in $M$ too. And so $\cup_{\alpha} V_{\alpha}^c$ is in too. By using De morgan’s law, $\cup_{\alpha} V_{\alpha}^c = (\cap_\alpha V_{\alpha})^c \in M$ and so $\cap_\alpha V_{\alpha} \in M$
4. If $A \in M, B \in M$ then $A-B \in M$
   • $A-B = A \cap B^c$이며 A,B가 M에 속하므로 $A^c, B^c$ 도 M에 속하며 3번 성질을 이용함으로써 $A-B, B-A$는 모두 M에 있음을 알 수 있다.

여기까지 직접 따라오면 알겠지만 $\sigma$ - algebra는 제법 체계적으로 짜여져 있다. 이렇게 구성된 집합은 나중에 Measure를 정의하는 데에 딱 들어맞음을 알 수 있다.

이러한 $\sigma$ - algebra는 유일하지 않다. 그런데 유일하지 않으면 체계적으로 생각하기도 애매하다. 따라서 여기에 몇가지 성질들을 추가해 유일성을 가진 $\sigma$ - alebra인 Borel Sets을 만들 수 있다. Borel Set의 정의는 다음과 같다.

Borel $\sigma$ algebra in X

• Smallest $\sigma$ -algebra which contains every open set in X

정의를 잘 살펴보면 topology의 원소가 open set이라고 불리며 모든 open set이 Borel $\sigma$ algebra에 포함되므로 Borel $\sigma$ algebra는 topology를 품고 있는 공간으로 생각할 수 있다.

거기에 더해 $\sigma$ - algebra는 여집합이 포함되므로 every closed set도 Borel $\sigma$ algebra에 포함되며, 차집합도 포함되므로 half open set 또한 포함된다. 따라서 Borel $\sigma$ algebra에는 사실상 생각할 수 있는 모든 것들이 포함된다고 생각하면 된다.(하지만 나중에 반례가 등장한다)

Borel $\sigma$ algebra의 원소 하나하나를 Borel set이라고 부른다.

마지막으로 Borel Function을 살펴보자.

Borel function

• For Borel space M and topological space N, any open set V in N and mapping $f:M\rightarrow N$,the function f is called Borel measurable if $f^{-1}(V)$ is in Borel set in M for every $V \subset N$

이는 위의 continuous function이나 measurable function에서 변형된 것이다. Borel set에는 open set이 포함되므로 모든 continuous function은 Borel Function이다. 그런데 pre-image가 open set이어도, closed set이어도, half-open set이어도 되므로 사실상 모든 함수가 Borel Function이 된다.

추가적으로 책에서는 Measurable function의 합성함수나 복소버전에 대한 다양한 정리들이 있다. 이 중에서 가장 범용적으로 쓰일만한 정리하나만 살펴보자.

Theorem

Let u,v be real measurable functions on a measurable space X, let $\psi$ be a continuous mapping of the plane into a topological space Y, and define $h(x) = \psi(u(x),v(x))$ for $x \in X$. Then $h: X \rightarrow Y$ is measurable

이를 이용하면 measurable function의 다양한 연산의 결과들이 measurable함을 이야기 할 수 있다. 예를 들어 $f+g, f \cdot g$ 등이 measurable 함을 알 수 있다.

앞선 0번 챕터에서 우리는 가능한 모든 함수에 대해서 적용가능한 적분을 찾는것을 목표로 한다고 했다. 따라서 거의 모든 함수가 속하는 Borel Function은 이러한 적분을 정의하기 위한 첫걸음인것이다. 다음으로 이러한 공간을 함수의 적분과 연결시켜주는 Simple Function에 대해서 알아보자.

B. Simple Function

공간을 입력값으로 받는 함수 중 가장 간단한 함수는 characteristic function이다. 이 간단한 함수를 이용함으로써 우리는 복잡한 함수로 까지 연역해갈 수 있다.

Characteristic Function

For a set E in X, a function $\chi_E (x) = \begin{cases}1 \quad \mbox{ if } x \in E \\ 0 \quad \mbox{ if } x \notin E \end{cases} $ is called characteristic function of the set E

만약 Set E가 Measurable Set일시, $\chi_E$는 Measurable Function이다.

---

pf)

Let V is open set in R containing 0 and not containing 1 , then $f^{-1}(V) = E^c$ which is measurable set

Let V is open set in R containing 1 and not containing 0 , then $f^{-1}(V) = E$ which is measurable set

Let V is open set in R containing 0,1, then $f^{-1}(V) = X$ which is measurable set

Let V is open set in R not containing 0,1 , then $f^{-1}(V) = X^c =\phi$ which is measurable set

So, in any case, if E is measurable, $\chi_E$ is measurable function.

---

이를 이용하면 Simple Function을 만들 수 있다. 엄밀하게 말하자면 Simple Function은 Range가 finitely many points로 구성된 함수를 의미한다. 이 경우, simple function s의 range는 ${\alpha_1 ,\alpha_2 ,…, \alpha_n}$이며, 이를 이용하면 특정 포인트를 함수값으로 가지는 정의역의 영역 $A_i = {x \in X : s(x) = \alpha_i }$를 만들 수 있다. 그러면 simple function은 다음과 동치가 된다. \(s = \overset{n}{\underset{i=1}{\sum}} \alpha_i \chi_{A_i}\) 즉, chracteristic function의 선형결합 꼴이 된다. Simple function의 예시는 다음과 같다. Simple Function은 Step function이라고도 불린다.

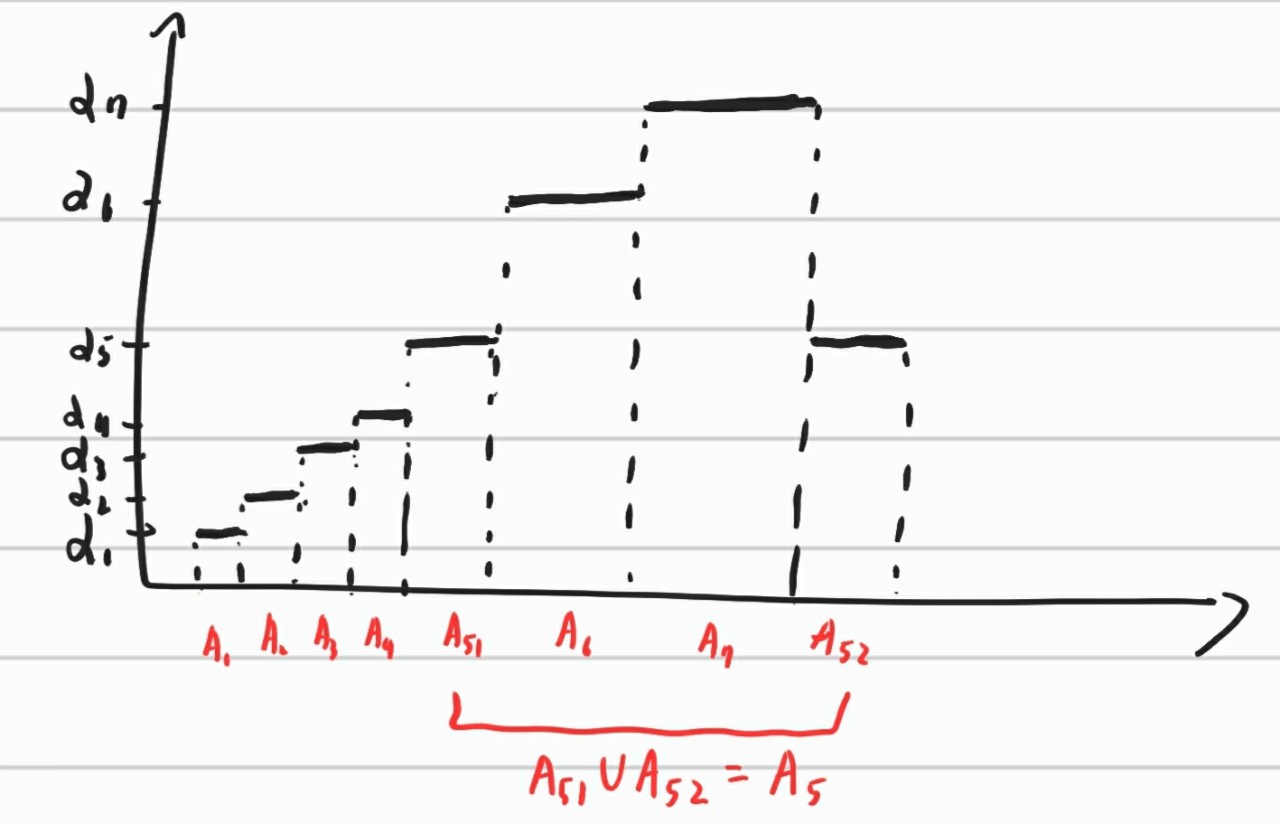
원래라면 경계점에 대해서 디테일하게 적어줘야 하지만 A공간은 open,closed,half-open 모두 가능하므로 디테일 하지 않아도 된다. measurable function의 합은 measurable하므로 simple function 역시 measurable하다.

이러한 simple function은 모든 positive measurable functional으로 근사시킬 수 있다. 즉 다음이 성립한다.

Theorem

Let $f: X \rightarrow [0,\infty)$ be measurable. Then there exists simple measurable function $s_n$ on X such that

• $0 \leq s_1 \leq s_2 \leq… \leq f$
• $s_n(x) \rightarrow f(x)$ as $n \rightarrow \infty$, for every $x \in X$

---

pf)

Set $\delta_n = 2^{-n}$. Let $k = k_n(t)$ be a integer satisfies $k \delta_n \leq t < (k+1)\delta_n$ for real number $t$. And define function $\psi_n$ as follow

$\psi_n(t) = \begin{cases} k_n(t)\delta_n \quad \mbox{ if } 0 \leq t < n \\ n \ \ \quad \quad \quad \mbox{ if } t \leq n \end{cases}$

$k_n(t)$ is a simple funcion obviously and $\psi(t) $ is a simple function because it just multiplies constant to $k_n(t)$. Therefore, $\psi(t)$ is as follow.

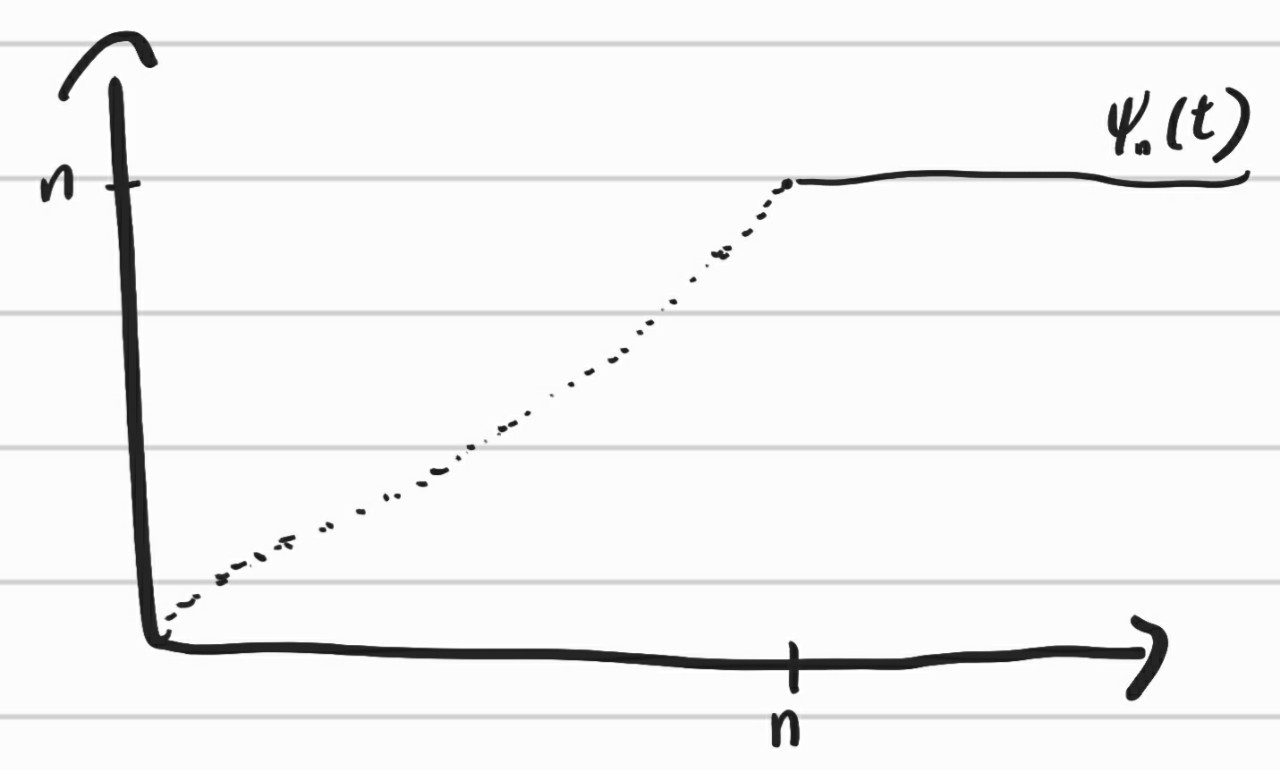
Because simple function is Borel function, $\psi_n$ is a Borel function too.

For this function, inequality $t-\delta_n <\psi_n(t) < t$ holds for every $t \in [0,n]$ and $\delta_n \rightarrow 0$ as $n \rightarrow \infty$. Therefore, $\psi_n(t) \rightarrow t$ as $n\rightarrow \infty$.

Then for any measurable function f, $s_n = \psi_n \circ f $ satisfies theorem’s condition and it is measurable too.

---

따라서 우리는 모든 positive measurable function을 simple function으로 근사시킬 수 있다. 여기서 positive라는 조건이 달려있지만 이는 trivial하다. 이는 르벡적분에서는 함수의 양수부분과 음수부분을 나누어서 다음과 같이 생각하는 관습이 있기 때문이다.

수학적으로는 다음과 같은 정의를 사용한다.
$f^+(x) = \max (f(x),0), f^-(x) = -\min(f(x),0)$
f^+과 f^- 둘 모두 positive 함수인 것에 주목하자. 거기에 더해 원본 함수는 $f = f^+-f^-$로 매우 간단하게 구할 수 있다. 따라서 step function을 이용하면 사실 상 모든 measurable function에 근사시킬 수 있다.

C. Measure

Definition of Measure

Measure(측도)의 개념은 Simple Function과 함께 르벡 적분을 완성하는 양대 축이라고 할 수 있다. 그 뿐 아니라 Measure 개념은 통계학의 확률 개념으로 확대될 수 있는 유용한 도구로 중요도가 매우 크다고 할 수 있다. Measure의 정의는 다음과 같다.

Measure (Positive Measure)

• Positive Measure : For a $\sigma$ - algebra M, a function $\mu: M \rightarrow [0, \infty)$ which is countably additive i.e. $\mu(\cup_i A_i) = \sum_i \mu(A_i)$ where $A_i$ is disjoint countable set is called by (Positive) Measure

  (For more detail, we shall assume that $\mu(A) < \infty$ for at least one $A \in M$)

• Measure Space : A measurable space which has a positive measure defined on its $\sigma$ - algebra
• Complex Measure : Measure which have its codomain as complex scalar field.

위와 마찬가지로 우리는 일반적으로 Positive Measure 이외의 Measure는 잘 고려하지 않으므로 Positive를 생략하고 그냥 Measure를 용어로 사용한다.

이 Measure 또한 공리적 정의를 가지고 있으며 $\sigma$ - algebra와 유사하게 공리로 부터 좀 더 다양한 성질을 유도해낼 수 있다.

Property of measure

• $\mu(\phi) = 0 $
  • Let $\mu (\phi)=k$ and $A_i = \phi$, then $\mu(\cup A_i) = \sum \mu(A_i) \Rightarrow \mu(\phi)=\sum \mu(\phi) \Rightarrow k =nk$. To make it true, k have to be 0.
• $\mu(\cup_i A_i) = \sum_i \mu(A_i)$ for finite i = 1,2,…,n
  • Set $A_{n+1} = A_{n+2} = … =\phi$
• $A \subset B$ implies $\mu(A) \leq \mu(B)$ if $A, B \in M$
• $\mu(A_n) \rightarrow \mu(A)$ as $n \rightarrow \infty$ if $A = \cup A_i , A_i \in M, A_1 \subset A_2 \subset A_3 \subset$ …
• $\mu(A_n) \rightarrow \mu(A)$ as $n \rightarrow \infty$ if $A = \cap A_i , A_i \in M, A_1 \supset A_2 \supset A_3 \supset$ …

Measure가 가지는 핵심적인 성질은 공간을 대상으로 하는 함수라는 점과 additive하다는 점이다. Additive는 일종의 벽돌을 생각하면 편할 수 있다. 어느 두 공간에 벽돌이 5개,10개씩 쌓여있다면 각각의 벽돌 측정치는 5,10이며 두 공간의 동시 측정치는 15이다. 사실 좀 더 추상적으로 Measure는 밀도에 비유된다. 그런데 Measure의 정의에 하나를 추가 하면 Probability의 공리와 일치하는 것을 알 수 있다.

Probability

• A function p is called probability if it holds following axiom
  • $0 \leq p(A_i) \quad A_i \subset X$ where $X$ is its domain
  • $p(\cup A_i) = \sum p(A_i)$ for disjoint $A_i$
  • $P(X) = 1$

즉, 확률도 Measure의 일종이다. 이것이 르벡적분으로 이어지면 확률을 다시금 해석할 수 있다.

Measure Space

일반적으로 Measure Space를 이야기 할때는 $(X, M, \mu)$로 표기한다. 첫번째 X는 대상이 되는 집합을 의미하며 두번째 M은 X에서 정의되는 $\sigma$ - algebra를 의미한다. 마지막으로 $\mu$는 이 $\sigma$ - algebra에서 정의되는 measure를 의미한다.

앞에서 Space의 정의를 어떠한 수학적 성질이 가미된 집합으로 내렸다. 따라서 Measure Space는 어떤 집합 X에 $\sigma$ - algebra와 measure의 성질을 특정해준 공간으로 이해할 수 있다.

그런데 해당 튜플 $(X,M,\mu)$의 경우, $\mu$의 정의역이 $M$이므로 $\mu$를 정의하면 $M$이 자동으로 정의되며, $X \in M$이므로 $M$의 원소 중 가장 큰 것이 $X$가 된다. 따라서 $\mu$만 정의하면 나머지는 불필요하다. 그럼에도 수학에서는 집합 $X$나 $M$을 강조하기 위해서나 일반적으로 사용되는 $\mu$가 존재해서 집합만 이야기해줘도 되는 등 여러가지 이유로 $(X,M,\mu),(X,M),X$ 등을 혼용해서 사용한다.

---

walter rudin,[real and complex analysis],McGrawHill