D. Lebesgue Integration
Lebesgue Integration
이제 여기까지 숙지했으면 르벡적분을 정의할 준비가 되었다. 르벡 적분의 정의는 몇가지 간단한 정의들의 집합으로 되어 있다. 천천히 따라가보자.
Lebesgue integration on positive simple funcition
- If $s: X \rightarrow [0, \infty)$ is a measurable simple function of the form $s = \overset{n}{\underset{i=1}{\sum}} \alpha_i \chi_{A_i}$ and $E$ is a member of $M$, then we define Lebesgue integration of $s$ on $E$ as follow
$\int_E s d \mu = \sum \alpha_i \mu(A_i \cap E)$
여기서 $A_i \cap E$는 trivial하며 간결함을 위해 E를 무시하고 생각할시 $\sum \alpha_i \mu(A_i)$로 간단해진다. 또한 $0 \cdot \infty =0$으로 정의되기에, $\mu(A_i) = \infty$라도 $\alpha_i =0$일시 해당 부분의 값은 0이다.Lebesgue integration on positive measurable function
If $f: X \rightarrow [0, \infty)$ is measurable and E is a member of M, then we define Lebesgue integration of $f$ on $E$ as follow
$\int_E f d \mu = \sup_{s \in S} \int_E s d \mu$
여기서 $S = {s \mid s \mbox{ is a simple function which holds an inequality } s \leq f}$이다.즉 이를 통해 우리는 모든 positive measurable function에 대한 lebesgue integration을 정의할 수 있다.
위의 정의를 살펴보면, 즉 르벡 적분은 Measureable한 함수를 Simple Function으로 근사시킨 뒤, Simple function이 단순히 직사각형막대의 모임이라는 성질을 이용함으로써 정의를 내리고 있음을 알 수 있다. 즉 아래 그림처럼 도식화 할 수 있다.
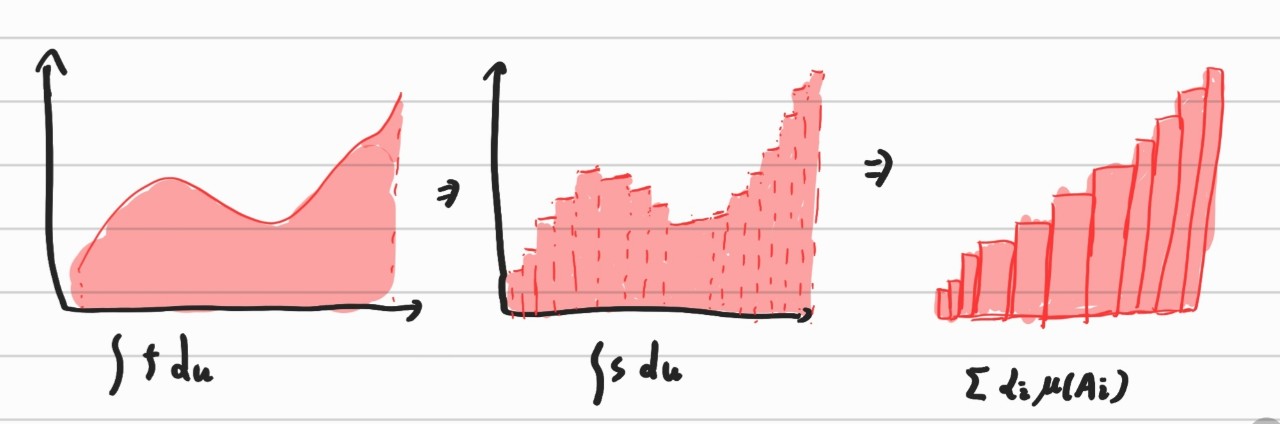
이 정의를 positive가 아니라 실수 전체나 복소수에 대해 정의되는 함수로 확장시키려면 두 함수의 합에 대한 적분이 두 함수 적분의 합이 됨을 보이면 되지만 이는 생각보다 간단한 일이 아니다. 따라서 아래 부분은 모두 비직관적인 해석학적인 접근이라 지루한 내용의 연속이다.
Property of Lebesgue Integration
- If $0 \leq f \leq g$ , then $\int_E f d \mu \leq \int_E g d \mu $
- If $A \subset B$ and $f \geq 0,$ then $\int_A f d \mu \leq \int_B f d \mu$
- If $f \geq 0$ and $c$ is a constant, $0 \leq c < \infty$, then $\int_E c f d \mu = c \int_E f d \mu$
- If $f(x) =0$ for all $x \in E$, then $\int_E f d \mu =0$, even if $\mu(E) = \infty$
- If $\mu(E)=0$, then $\int_E f d \mu =0$, even if $f(x) =\infty$ for every $x \in E$
- If $f \geq 0$, then $\int_E f d \mu = \int_X \chi_E f d \mu$
이들은 모두 정의를 통해 간단하게 유도할 수 있다. 특히 마지막 성질을 이용하면 정의를 그대로 유지한채 적분의 범위를 컨트롤 할 수 있다. 증명을 위해서는 $\chi_A \cdot \chi_E = \chi_{A \cap E}$ 임을 이용하자.
다음으로 나올 것은 해석학적으로 르벡적분의 가장 중요한 정리들이다. 증명이 지루할 수 있으니 증명부분은 건너뛰어도 상관없을 것 같다.
Proposition 1
- Let s and t be nonnegative measurable simple functions on X. For $E \in M$, define $\psi(E) = \int_E s d\mu$. Then $\psi$ is a measure on R and $\int_X (s+t) d \mu = \int_X s d \mu + \int_X t d\mu$
Proposition 2. Lebesgue’s Monotone Convergence Theorem
Let ${f_n}$ be a sequence of measurable functions on X, and suppose that
- $0 \leq f_1(x) \leq f_2 (x) \leq … \leq \infty$ for every $x \in X$
- $f_n (x) \rightarrow f(x)$ as $n \rightarrow \infty$, for every $x \in X$
Then f is measurable and $\int_X f_n d \mu \rightarrow \int_X f d \mu$ as $n \rightarrow \infty$
Proposition 3
- For any measurable function $f_1$ and $f_2$, $\int_X (f_1 + f_2 )d \mu = \int_X f_1 d\mu +\int_X f_2 d\mu$
Propostion 4
- If $f_n : X \rightarrow [0, \infty]$ is measurable, for n = 1,2,3,…., and $f(x) = \sum_n f_n(x) \quad (x \in X),$ then $\int_X f d \mu = \sum_n \int_X f_n d \mu$
Proposition 5. Fatou’s Lemma
- If $f_n : X \rightarrow [0, \infty]$ is measurable, then $\int_X (\lim \int f_n) d \mu \leq \lim \inf \int_X f_n d\mu$
Proposition 6.
- Let f be nonnegative measurable functions on X. For $E \in M$, define $\psi(E) = \int_E f d\mu$. Then $\psi$ is a measure on R and $\int_X g \ d \psi = \int_X gf\ d\mu$ for every measurable g on X with range $[0, \infty]$
pf 1)
Let $E_1, E_2 ,…$ are disjoint members of $M$ and $\cup E_i = E$. Then
$\psi( \cup E_j) = \psi(E) = \int_E s d\mu = \sum_i \alpha_i \mu(A_i \cap E) = \sum_i \sum_j \alpha_i \mu(A_i\cap E_j)$
$ = \sum_j \sum_i \alpha_i \mu(A_i \cap E_j) = \sum_j \int_{E_j}s d\mu = \sum_j \psi(E_j)$
Therefore, $\psi$ is a measure on R.
Let $t = \sum_j \beta_j \chi(B_j)$ and $E_{ij} = A_i \cap B_j$.. then $s+t = \sum_i \sum_j (\alpha_i +\beta_j) \chi(E_{ij})$
So, $\int_{E_{ij}} (s+t) d \mu = (\alpha_i +\beta_j) \mu(E_{ij}) = a_i \mu(E_{ij})+\beta_j\mu(E_{ij}) = \int_{E_{ij}}s d \mu +\int_{E_{ij}}t d \mu$
Because $\psi(X) = \psi(\cup \cup E_{ij}) = \sum \sum \psi(E_{ij})$ above equaility holds for $E_{ij} \rightarrow X$
Therefore, $\int_X (s+t) d \mu = \int_X s d \mu + \int_X t d\mu$
pf 2)
Because $\int_X f_n d \mu$ is monotone increasing, there is a $\alpha \in [0,\infty]$ such that $\int_X f_n d \mu \rightarrow \alpha$ as $n\rightarrow \infty$.
$\int_X f_n d \mu \leq \int_X f d \mu \rightarrow \alpha \leq \int_X f d \mu$ ——(A)
Let s be any simple function such that $0 \leq s \leq f, c$ be a any constant in $[0,1]$. Define $E_n = {x : f_n(x) \geq c s(x)}$ then $E_n$ is measurable set and $X = \cup E_n$ and $ E_1 \subset E_2 \subset E_3 \subset…$. Then
$\int_X f_n d \mu \geq \int_{E_n} f_n d\mu \geq c \int_{E_n} s d \mu$
Let $n \rightarrow \infty$ , then
$\alpha \geq c \int_{X} s d \mu$
$\Rightarrow \alpha \geq \int_X s d\mu$ $(\because \mbox{it hold for every }1\geq c)$
$\rightarrow \alpha \geq \int_X f d \mu$ $(\because \mbox{it hold for every }f\geq s)$ —–(B)
By A,B, $\int_X f d \mu = \alpha \leftarrow \int_X f_n d\mu$
pf 3)
Let $s_{1i} \rightarrow f_1 , s_{2i}\rightarrow f_2$ be simple function, then we know $s_{1i} + s_{2i} \rightarrow f_1 + f_2$ and using above proposition, we get the results.
pf 4)
Let $g_n = \sum_{i=1}^n f_i$. Then,$ g_n \rightarrow f$ and $\sum_{i=1}^n \int f_n d\mu=\int \sum_{i=1}^n f_n d \mu=\int g_n d \mu \rightarrow \int f d \mu$ by using propostion 2,3
pf 5) 생략.
pf 6)
Let $E_1, E_2 ,…$ are disjoint members of $M$ and $\cup E_i = E$. Then $\chi_E f = \sum_j \chi_{E_j}f$ and $\psi(E) = \int_X \chi_E f \ d \mu, \psi(E_j) = \int_X \chi_{E_j} f \ d \mu$
Then we can prove $\psi(E) = \sum \psi(E_j)$ and $\psi$ is a measure.
And we can see that $\int_x \chi(E) d \psi = \sum_i \chi(E_i) \psi(A_i) = \sum_i \sum_j \chi(E_i) \beta_{fi} \mu(A_i \cap B_j) = \int_x \chi(E_i)f(x) d \mu$.
Now, by linear combination, we can construct any measurable function $g$ with $\chi$
이들은 르벡적분이 해석학적으로 가지고 있는 성질에 대한 정리이다. 특히 2번 정리는 Measurable function이 그 자체로 completeness를 가지고 있으며, Integration operator가 그자체로 연속 함수임을 함의한다.
이 중 6번 정리는 통계학에서 자주 볼 수 있는 등식인 $\int g(x) d F(x) = \int g(x)f(x) \ dx$를 함의한다.
다음으로 3번 정리를 이용함으로써 우리는 positive measurable function에서 complex measurable function으로 확대 할 수 있다.
Lebesgue integration on positive measurable function
- For any complex measurable function f, we can decompose it four positive measurable function as $f = u + iv = (u^+-u^-) + i(v^+-v^-)$ where $u^+,u^-,v^+,v^-$ is positive measurable function.
- Then $\int_E f\ d \mu = \int_E u^+\ d \mu- \int_E u^-\ d \mu + i\int_E v^+\ d \mu- i\int_E v^-\ d \mu $
마지막으로 또 다른 중요한 정리를 보고 마무리 하자.
Definition
- $L^1(\mu),L^2(\mu)$는 함수들을 모아놓은 공간이며 각각 ${f \mbox{ is measurable}:\int \mid f\mid d \mu <\infty } ,{f\mbox{ is measurable}:\int \mid f\mid^2 d \mu <\infty }$을 의미한다.
Lebesgue’s Dominated Convergence Theorem
- Suppose ${f_n}$ is a sequence of complex measurable functions on X such that $f(x) = \lim f_n(x)$ exists for every $x \in X$. If there is a function $g \in L^1(\mu)$ such that $\mid f_n(x) \mid \leq g(x) \quad (n=1,2,3,…;x \in X)$,then
- $f \in L^1(\mu)$
- $ \lim \int_X \mid f_n-f\mid d \mu =0$
- $\lim \int_X f_n d \mu = \int_x \lim f_n d \mu$
아직은 다루지 않았지만 $L^1(\mu)$ 공간의 Standard Norm은 $\parallel f \parallel = \int_X \mid f \mid d\mu$로 정의되므로 주어진 조건 $\mid f_n (x) \mid \leq g(x)$는 $\parallel f_n \parallel \leq \parallel g\parallel \leq \infty$ 이므로 수열 $f_n$이 Bounded 하다는 조건으로 이해할 수 있다. 따라서 1번 정리는 이 L-1공간이 complete하다는 것을 함의하며 3번 정리는 이경우 lim와 integral을 commute 할 수 있음을 의미한다.
E. Set of Measure Zero
이제 르벡적분의 정의와 해석학적 성질에 대해서는 알아보았다. 그런데 측도가 0인 공간(Measure Zero)은 해석학적으로 함의하는 바가 크다. 이를 이용하면 여러가지 유용한 수학적 개념을 만들어 낼 수 있다.
그 중 하나가 각 학계에서 조금만 수학적으로 들어가도 많이 나오는 개념인 Almost Everywhere가 있다.
Definition
- Some property is said to be “hold almost everywhere on E” when there exists an $N \in M$ such that $\mu(N)=0 ,N \subset E,$ and $P$ holds at every point of $E-N$
쉽게 말하자면 p가 almost everywhere on E에서 성립한다는 말은 E의 Measure 0 부분에서는 성립안해도 되고 나머지에선 성립해야 한다는 것을 의미한다. Measure 0인 부분은 연구의 관심 대상이 아니거나 전체에서 비중이 0에 가까운 부분으로 이해하면 된다.
예를 들어 $f(x) =1, g(x) = \begin{cases} 1 \quad \mbox{ if} x \neq 0 \\ 0 \quad \mbox{ if } x = 0 \end{cases}$의 경우, f와 g는 $x=0$인 부분을 제외하고 $f=g$이며 $x=0$ 에서는 $f \neq g$이지만 일반적으로 실수에서 사용하는 measure는 point 각각의 measure를 0으로 두므로 (연속형 확률변수 X에 대해 X=0일 확률이 0인 논리와 같다.) $f=g \quad a.e. \mbox{ on } R$이라고 이야기 할 수 있다.
이 Almost Everywhere 컨셉을 이용하면 다음과 같은 정리들을 유도할 수 있다.
Theorem
Suppose ${f_n}$ is a sequence of complex measurable functions defined a.e. on X such that $\sum \int_X \mid f_n \mid d \mu < \infty$, then
$f(x) = \sum f_n(x)$ converges for almost all $x, f \in L^1(\mu)$ and $\int_X f d \mu = \sum \int_X f_n d \mu$
Suppose $f:X \rightarrow [0,\infty]$ is measurable, $E \in M$ and $\int _E f d \mu =0.$ Then $f =0 \ a.e.$ on $E$
Suppose $f \in L^1(\mu)$ and $\int_E f d \mu =0$ for every $E \in M$. Then $f=0 \ a.e.$ on $X$
Suppose $f \in L^1(\mu)$ and $\mid \int_X f d \mu \mid = f_X \mid f \mid d \mu$ . Then there is a constant $\alpha$ such that $\alpha f = \mid f \mid a.e.$ on $X$
Suppose $\mu(X)<\infty, f\in L^1(\mu), S$ is a closed set in the complex plane, and the averages $A_E(f)=\frac{1}{\mu(E)}\int_E f d \mu$ lies in $S$ for every $E \in M$ with $\mu(E)>0$. Then $f(x) \in S$ for almost all $x \in X$
증명은 생략하자. 힘들다..
2번 정리를 적분값이 0이면서 f가 0인 상수함수는 아닌 함수를 생각할 수 있다. 이 경우, 앞서 얘기했던 입력값이 유리수있때 1이고 무리수 일때 0인 디리클레 함수의 적분값은 유리수 집합은 결국 point의 countable한 집합이므로 measure가 0이며 따라서 디리클레 함수의 적분값은 0임을 알 수 있다.
마지막 정리는 평균값의 정리의 적분형태이다.
그런데 이 Measure 0에 대해 measure의 공리를 이용하면 $\mu(N)=0$에 대해 N의 부분집합 E의 측도 또한 0이 되어야 함을 알 수 있다. 그렇다면 만약 주어진 $\sigma$ -algebra가 N만 포함하고 E를 포함하지 않을시 이 E에 대해서도 측도를 이야기 해줄 수 있으므로 기존의 $\sigma$-algebra보다 더 확대된 $\sigma$-algebra를 얻어낼 수 있음을 알 수 있다. 이를 $\sigma$-algebra의 $\mu-$completion이라고 한다. 구체적으로 다음과 같은 프로세스를 의미한다.
$\mu $- completion
- Let $(X,M,\mu)$ be a measure space, let $M^\ast$ be the collection of all set $E \subset X$ which there exist sets $A,B \in M$ such that $A \subset E \subset B$ and $\mu(B-A)=0$. And define $\mu(A)=\mu(E)$. Then $M^\ast$ is a $\sigma$- algebra, and $\mu$ is a measure on $M^\ast$
ex)
Let $X = {1,2,3,4,5}$, and $M = {\phi,X,{1,2,3},{4,5}}$ and each measure as ${0,3,3,0}$
해당 집합에 대해서 우리는 1,2,3의 각 측도가 얼마인지는 알 수 없지만 ${4},{5} \subset {4,5}$ 이며 $\mu({4,5})=0$이므로 각각 4,5의 측도가 0임은 알 수 있다.
거기에 더해 $\sigma$-algebra의 정의에 따라 4,5의 여집합인 ${1,2,3,5},{1,2,3,4}$ 또한 $\sigma$-algebra에 속해야 한다는 것을 알 수 있으며 measure의 공리인 $\mu({1,2,3,4,5})=\mu({1,2,3,4})+\mu({5})$를 이용하면 ${1,2,3,4}$의 측도가 3인것도 알 수 있다.
이러한 방식으로 주어진 M보다 더 많은 원소를 가지고 있는 $M^\ast$을 만들 수 있고 이는 다음과 같다.
$M^\ast = {\phi,{4},{5},{4,5},{1,2,3},{1,2,3,4},{1,2,3,5}{1,2,3,4,5}}$
$\mu ={0,0,0,0,3,3,3,3}$
여기까지가 Abstract Integration의 내용이며 Rudin 책이 다루고 있는 1장이다. 공부할때도 죽을만큼 힘들었지만 정리를 하고나니 양이 말도안되게 많아서 왜 힘들었는지 알겠다.. 어쨋든 1장만으로도 지금까지 통계학에 나왔던 많은 부분들을 커버할 수 있었다. 다음 포스팅은 Positive Borel Measures로 Borel Measure에 대해서 좀 더 자세하게 보는 듯 하다.
walter rudin,[real and complex analysis],McGrawHill
