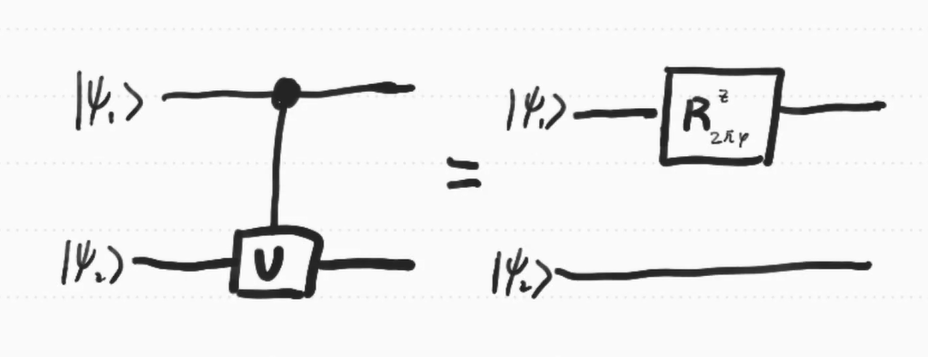$\def\ket#1{\mid #1 \rangle}$
Chapter 4. Quantum Phase Estimation and Quantum Distance Measure
1. Quantum Phase Estimation
양자 게이트는 행렬로 표현되는데, 각 큐빗은 게이트를 지나기 전에도, 후에도 확률진폭 제곱의 총합은 1 이어야한다. 따라서 큐빗 상태의 Norm은 1이며 이는 변하지 않는다.
이것이 함의하는 바는 게이트 행렬의 모든 아이젠 밸류의 절댓값이 1임을 의미한다. 따라서 다음과 같이 표현할 수 있다.
$\lambda =e^{2\pi \psi i} \mbox{ where } \psi \in [0,1)$
이때 각각의 양자게이트에 대한 $\psi$(phase)를 추정함으로써 게이트의 아이젠밸류를 따오는 것이 바로 Quantum Phase Estimation이다.
Unitary Matrix의 적용
양자게이트 $U$의 아이젠 밸류를 $e^{2 \pi \psi i}$로 , 아이젠 벡터를 $ \mid \Psi \rangle$로 둘시 다음이 성립한다.
$U \mid \Psi \rangle = e^{2\pi \psi i }\mid \Psi \rangle$
이를 응용하면 양자게이트를 $2^m$ 만큼 통과 시켰을때를 다음과 같이 일반화 할 수 있다.
$U \mid \Psi \rangle = e^{2 \pi \psi i}\mid \Psi \rangle$
$U^2 \mid \Psi \rangle = U e^{2\pi \psi i}\mid \Psi \rangle = e^{2\times2\pi \psi i}\mid \Psi \rangle$
$\cdots$
$U^{2^{j}} \mid \Psi \rangle= e^{2^{j+1}\pi \psi i}\mid \Psi \rangle$
또,아이젠백터에 적용되는 양자게이트는 $U=e^{2 \pi \psi i}I$와 똑같이 적용되므로 다음과 같이 단순화할 수 있다.
$e^{2\pi \psi i} \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] = \left[ \begin{array}{cc} e^{2\pi \psi i} & 0 \\ 0 & e^{2\pi \psi i} \end{array}\right] $
따라서 아이젠벡터가 인풋으로 들어오는 경우에 한해 다음과 같이 바꿀 수 있다.
pf)
Let $\ket \psi_1 = a \ket 0+ b \ket 1$
then $cU(\ket {\Psi_1},\ket {\Psi_2}) = a\ket 0\otimes \ket {\Psi_2}+b\ket 1 \otimes U \ket {\Psi_2} \\ \qquad \qquad \qquad \ = a\ket 0\otimes \ket {\Psi_2}+b\ket 1 \otimes e^{2 \pi \Psi i } \ket {\Psi_2} \\ \qquad \qquad \qquad \ =(a \ket 0 +be^{2 \pi \Psi i}\ket 1 )\otimes \ket {\Psi_2} \\ \qquad \qquad \qquad \ =R_{2 \pi \psi} \ket {\Psi_1} \otimes \ket{ \Psi_2} $
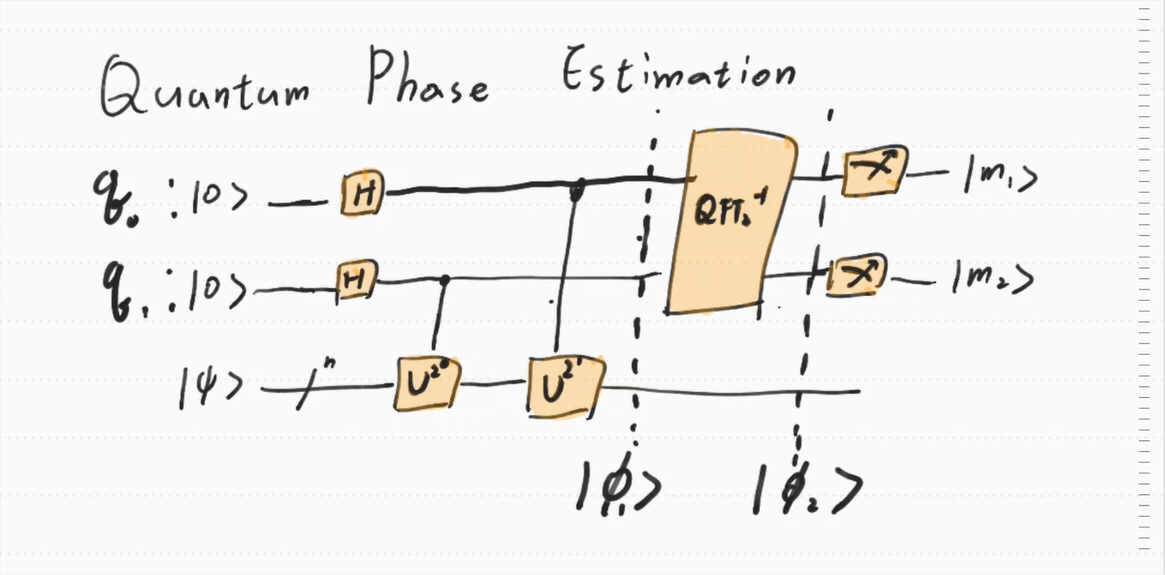
Quantum Phase Esitmation Circuit
이제 이를 이용한 Quantum Phase Estimation Circuit은 다음과 같다.
이는 2-qubit Quatum Gate의 Quantum Phase Estimation Circuit이다. 이를 추적해나가보자.
우선 $\ket {\phi_1}$에서의 상태를 살펴보기 위해 $q_0,q_1$를 따라가보자.
$q_0$의 경우
$cU^{2^1}(H\ket 0 , \ket \Psi) = cU^{2^1}(\frac{1}{\sqrt{2}}(\ket 0 + \ket 1 ),\ket \Psi) \\ \qquad \qquad \qquad \quad \ = \frac{1}{\sqrt{2}}(\ket 0 \ket \Psi + \ket 1 U^{2^1}\ket \Psi) \\ \qquad \qquad \qquad \quad \ =\frac{1}{\sqrt{2}}(\ket 0 \ket \Psi + \ket 1 e^{2^ 2 \pi \psi i }\ket \Psi) \\ \qquad \qquad \qquad \quad \ = \frac{1}{\sqrt{2}}(\ket 0 + e^{2 \pi 2^1 \psi i }\ket 1 ) \otimes\ket \Psi)$
$q_1$도 유사하게 다음과 같은 결과가 나온다.
$cU^{2^0}(H\ket 0 , \ket \Psi)= \frac{1}{\sqrt{2}}(\ket 0 + e^{2 \pi 2^0 \psi i }\ket 1 ) \otimes\ket \Psi)$
따라서 $\ket \phi_1$는 다음과 같다.
$\ket \phi_1 = \frac{1}{2}(\ket 0 + e^{2 \pi 2^1 \psi i }\ket 1 ) \otimes (\ket 0 + e^{2 \pi 2^0\psi i }\ket 1 ) \otimes \ket \Psi \\ \quad \ \ = \frac{1}{2}(\ket{00}+e^{2\pi2^0\psi i}\ket{01}+e^{2 \pi 2^1 \psi i }\ket{10}+e^{2 \pi (2^2-1) \psi i}\ket{11}) \otimes \ket \Psi\\ \quad \ \ =\frac{1}{\sqrt{2}^2} \sum_{j=0}^{2^2-1}e^{2\pi j \psi i} \ket j_2 \otimes \ket \Psi$
다음으로는 Inverse QFT Gate가 있는데 우선 이것이 어떻게 작동하는 지부터 살펴보자. $N=2^n$의 Qubit에 대해 Inverse -Quantum Fourier Transformation은 다음과 같이 작동한다.
$\ket \chi = \sum_{j=0}^{2^2-1}a_j\ket j _2$
$QFT^{-1}(\ket \chi)=\frac{1}{\sqrt{2^2}}\overset{2^2-1}{\underset{j=0}{\sum}}\overset{2^2-1}{\underset{k=0}{\sum}}a_ke^{-\frac{2 \pi ijk}{2^2}} \ket j _2$ ($a_k = \frac{1}{\sqrt{2^2}}e^{2 \pi j \psi i}$)
따라서 $\ket{\phi_2} = QFT^{-1}(\frac{1}{\sqrt{2}^2} \sum_{j=0}^{2^2-1}e^{2\pi j \psi i} \ket j_2) \otimes \ket{\Psi_2}$는 다음과 같다.
$QFT^{-1}(\frac{1}{\sqrt{2}^2} \sum_{j=0}^{2^2-1}e^{2\pi j \psi i} \ket j_2) = \frac{1}{2^2}\overset{2^2-1}{\underset{j=0}{\sum}}\overset{2^2-1}{\underset{k=0}{\sum}} e^{2 \pi j \psi i} e^{-\frac{2 \pi ijk}{2^2}} \ket j _2 \\ \qquad\qquad\qquad\qquad\qquad\qquad\quad= \frac{1}{2^2}\overset{2^2-1}{\underset{j=0}{\sum}}\overset{2^2-1}{\underset{k=0}{\sum}} e^{-\frac{2 \pi k i}{2^2} (j- 2^2\psi) } \ket j _2$
이 결과물을 해석하면 상태 $\ket j_2$의 확률진폭은 $\frac{1}{2^2}\overset{2^2-1}{\underset{k=0}{\sum}} e^{-\frac{2 \pi k i}{2^2} (j- 2^2\psi) }$이라고 말할 수 있다.
이를 $2^m$- Qubit으로 일반화하면 다음과 같다.
$\ket {j}$의 확률진폭 = $\frac{1}{2^m}\overset{2^m-1}{\underset{k=0}{\sum}} e^{-\frac{2 \pi k i}{2^m} (j- 2^m\psi) }$
이 결과물을 어떻게 해석할 수 있을까?
위의 확률진폭은 k라는 확률변수의 평균값이므로 $E(e^{-\frac{2 \pi k i}{2^m} (j- 2^m\psi) })$의 추정치이며 이는 결국 j의 확률진폭의 추정치라고 말할 수 있다.
따라서 $\hat{ p(j) } = \mid \frac{1}{2^m}\overset{2^m-1}{\underset{k=0}{\sum}} e^{-\frac{2 \pi k i}{2^m} (j- 2^m\psi) } \mid ^2 = \frac{1}{2^{2m}}\mid\overset{2^m-1}{\underset{k=0}{\sum}} e^{-\frac{2 \pi k i}{2^m} (j- 2^m\psi) } \mid ^2$이다.
결국 해당값이 추정하는 대상은 대략 $e^{-\frac{2 \pi k i}{2^(m-1)} (j- 2^m\psi)}$이다. 이는 정규분포의 확률밀도 함수와 매우 흡사하며 $j=2^m \psi$에서 가장 높은 확률값을 가지게 될 것이다.
따라서 해당 게이트를 여러번 돌려서 나오는 j의 최빈값은 $2^m \psi$일 것이며 $\psi$는 0에서 1사이의 수이므로 결과물 j에 대해 $\frac{j}{2^m}=\hat{\psi}$를 추정할 수 있다.
여기서 j를 주목하자.
- j는 $0 \sim 2^m-1$ 까지를 값으로 가지므로 $\frac{j}{2^m}$은 $0\sim \frac{2^m-1}{2^m} \approx1$ 까지를 값으로 가진다. 페이즈 파라미터인 $\psi$는 스케일링 상수인 $2\pi$과 함께 있으므로 0~1사이의 값으로 모든 경우를 다 다룰 수 있다. 따라서 $\frac{j}{2^m}$로 $\psi$를 추정해낼 수 있는 것이다.
- j는 각각의 상태쌍에 이름을 붙인 것이다. 예를 들어 5개의 Qubit이 있을 때, $\ket {j}$에 대해 j에 따라 다음과 같은 값이 붙는다.
$\ket{0} = \ket {00000}$
$\ket{1} = \ket{00001}$
$\ket{2} = \ket{00010}$
$\ket{3} = \ket{00011}$
$\ket{4} = \ket{00100}$
…
$\ket{30} = \ket{11110}$
$\ket{31} = \ket{11111}$
다음으로 각각의 수를 2진법으로 바꾸어보자.
$0 = 0_{(2)}$
$1 = 1_{(2)}$
$2 = 10_{(2)}$
$3 = 11_{(2)}$
…
$31 = 11111_{(2)}$
$32 =100000_{(2)}$
놀랍게도 위에서 매긴 수치와 일치한다. (배경 지식에 따라 놀랍진 않을 수 도 있다.)
이러면 $\frac{j}{2^m}$의 값은 다음과 같은 의미를 가진다.
$0.b_1b_2b_3b_4…b_m$ $(b_i \in {0,1} \quad \forall i)$ ($b_i$는 $\ket {q}_{2^m}$의 i번째 큐빗의 관측값)
예를들어, 해당 회로를 여러번 돌림으로써 다음과 같은 큐빗 상태를 최빈값으로 얻었다고 가정하자.
$\ket{110010110011}$
그렇다면 해당 회로가 추정한 아이젠 밸류의 추정치는 $0.110010110011_{(2)}$인 것이다.
물론 아이젠밸류는 보통 무한대인 반면 QPE 알고리즘은 사용된 큐빗개수 m에 따라 10^{-m} 자리수 까지만 추정을 할 수 있기 때문에 정확한 추정을 하는 것은 거의 불가능하다.
따라서 오차율이 있는데 이는 반복측정을 통해서 낮출 수 있다. 또 m을 늘림에 따라서 근사 지점까지 추정을 할 수 있다.
여기까지 봤을때 의문이 들 수 있는 지점은 아이젠벡터 $\ket{\psi}$를 알고있다고 가정한다는 것이다. 다행히 실제 알고리즘을 짤때는 이러한 점을 고려하고 짠다.
이를 활용한 알고리즘으로 HHL Algorithm For Linear Solver를 들 수 있다. Linear Solver라 함은 말 그대로 특정 행렬 A와 벡터 b에 대해 $Ax=b$를 만족하는 x를 찾는 것이다. 이에 대해서는 다음 포스팅에 자세히 다루었다.
2. Quantum Distance Measure
두 상태 $\ket{\psi _\alpha}, \ket{\psi_b}$를 생각해보자. 두 상태의 유사도를 측정할 가장 좋은 방법은 무엇일까?
일반적인 거리 척도로 가장 많이 쓰이는 L2- Distance에 한해서는 내적을 통해 매우 쉬운 방식으로 측정이 가능하다.
$\mid \ket{\psi_\alpha} - \ket{\psi_{\beta}}\mid_2^2 = (\ket{\psi_\alpha} - \ket{\psi_{\beta}})^t(\ket{\psi_\alpha} - \ket{\psi_{\beta}}) \\ \qquad\qquad \qquad= \langle \psi_{\alpha},\psi_\beta \rangle - \langle \psi_{\alpha},\psi_\alpha \rangle-\langle \psi_{\alpha},\psi_\beta \rangle+\langle \psi_{\beta},\psi_\beta \rangle \\ \qquad\qquad \qquad= 2-2RE{\langle \psi_{\alpha},\psi_\beta \rangle}$
Quantum State는 Unitary Gate를 활용해서 $\ket {\psi_\alpha} = U_\alpha \ket 0 , \ket {\psi_\beta} = U_\beta \ket 0$를 취해줌으로써 만들어 낼 수 있다. 즉, 각 State는 일대일로 대응 Unitary Gate를 가진다고 말 할수 있겠다.
이를 활용해, Quantum State는 Hadamard Test와 SWAP Test를 통해서 계산할 수 있다.
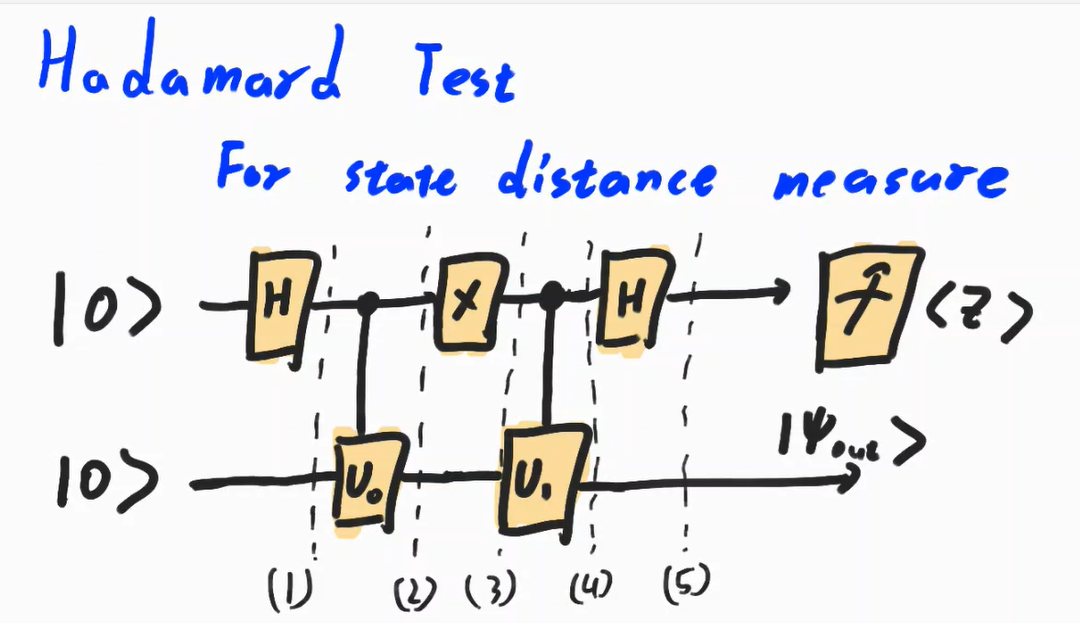
Hadamard Test
Hadamard Test의 Circuit은 위와 같다.
이를 1번 부터 Tracking해보자.
-
$\ \ket{\psi_1} = \frac{1}{\sqrt 2}( \ket 0 + \ket 1) \ket 0 \\ \qquad \propto \ket {00} + \ket {10}$
-
$\ \ket {\psi_2} = cU_{\alpha} (\ket {00} + \ket {10})\\ \qquad = \ket{00}+\ket{1 \ \psi_\alpha}$
-
$\ \ket{\psi_3} = \ket{10}+\ket{0\psi_\alpha}$
-
$\ket{\psi_4} = cU_{\beta}(\ket{10}+\ket{0\psi_\alpha}) \\ \qquad = \ket{1 \psi_\beta} + \ket{0\psi_\alpha}$
-
$\ \ket{\psi_5} = (\ket{0} + \ket{1})\ket{\psi_\alpha} +(\ket 0 - \ket 1)\ket {\psi_\beta} \\ \qquad \propto \frac{1}{2}\ket{0}(\ket{\psi_\alpha}+\ket{\psi_\beta})+\frac{1}{2}\ket{1} (\ket{\psi_\alpha} - \ket{\psi_\beta}) $
-
Measure :
$p(0) = \frac{1}{2}^2\mid\ket{\psi_\alpha}+\ket{\psi_\beta}\mid^2 = \frac{1}{2} + \frac{1}{2}Re{\langle \psi_\alpha \mid \psi_{\beta} \rangle}$
$p(1) = \frac{1}{2}^2\mid\ket{\psi_\alpha}+\ket{\psi_\beta}\mid^2 = \frac{1}{2} - \frac{1}{2}Re{\langle \psi_\alpha \mid \psi_{\beta} \rangle}$
즉 Circuit에 Qubit을 여러번 통과시킨 후 0과 1이 측정되는 비율을 계산함으로써, 두 큐빗의 거리를 측정할 수 있다.
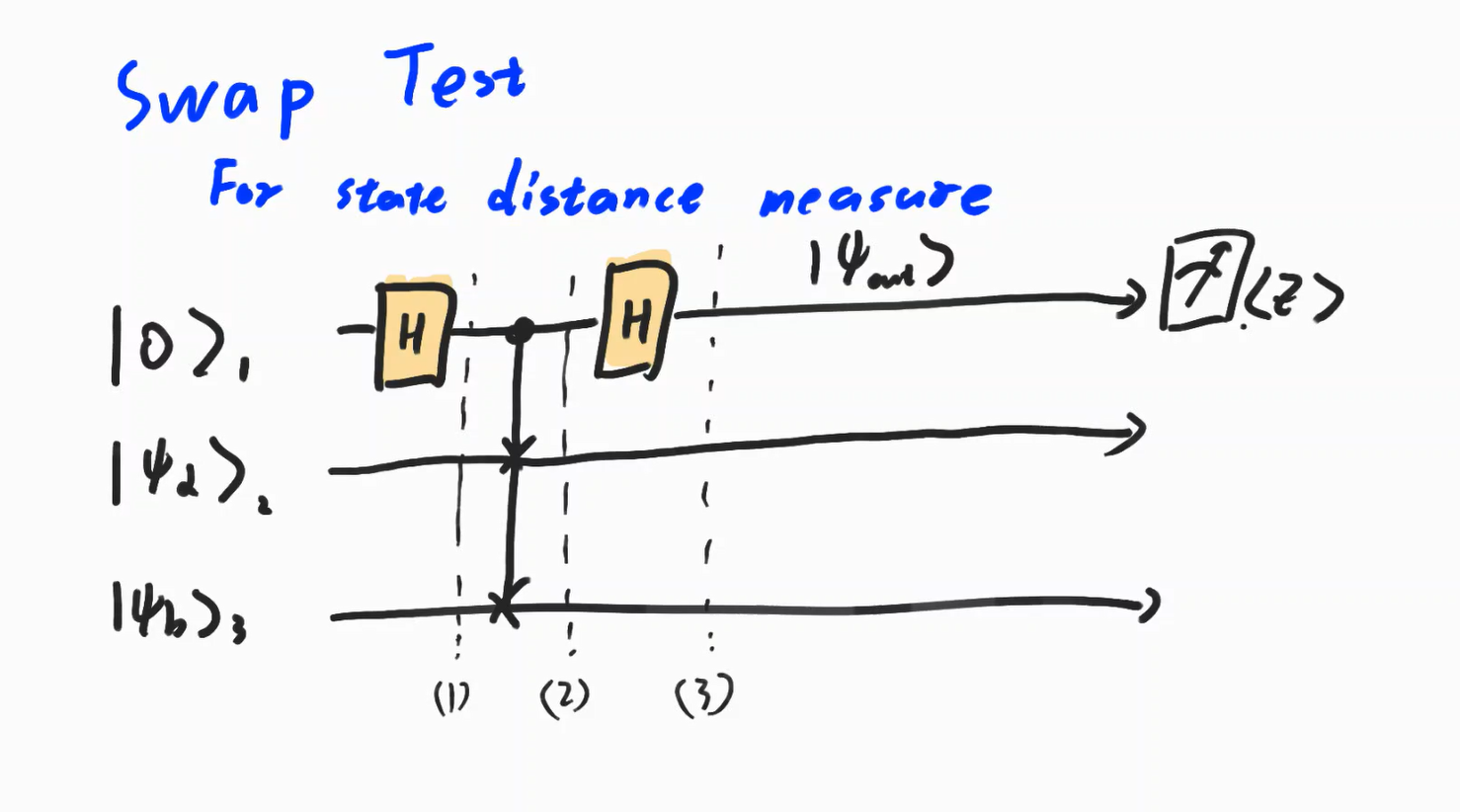
SWAP Test
Hadamard Test와 똑같은 역할을 Swap Test를 통해서도 진행할 수 있다. 이 또한 과정을 Tracking 해보자.
-
$\ket{\psi_1} = (\ket 0 + \ket 1)\ket{\psi_\alpha \psi_\beta}$
-
$\ket{\psi_2} = Fredkin(\ket{\psi_1}) \\ \ \quad = \ket{0\psi_\alpha\psi_\beta}+\ket{1\psi_\beta\psi_\alpha}$
-
$\ket{\psi_3} = \ket{0}(\ket{\psi_\alpha \psi_\beta}+\ket{\psi_\beta \psi_\alpha}) + \ket{1}(\ket{\psi_\alpha \psi_\beta}-\ket{\psi_{\beta}\psi_{\alpha}} $
-
Measure:
$p(0) = \frac{1}{2} + \frac{1}{2}\mid\langle \psi_\alpha, \psi_ \beta \rangle\mid^2$
$p(0) = \frac{1}{2} - \frac{1}{2}\mid\langle \psi_\alpha, \psi_ \beta \rangle\mid^2$
이를 이용하여 위와 같은 거리값을 유도해낼 수 있다.
위를 통해 큐빗 간의 L2-거리를 잴 수 있는데, 큐빗 State에 데이터의 상태를 녹여냄으로써, 데이터 포인트 간의 L2거리를 잴 수 있겠다. 이를 응용하면 L2거리가 포함되는 무수히 많은 알고리즘을 빠르게 풀어낼 수 있다.
Sutor, R. (2019). Dancing With Qubits. Birmingham,UK:Packt
Bernhardt, C. (2019). Quantum computing for everyone. Boston, Massachusetts:The MIT Press