$\def\ket#1{\mid #1\rangle}$
1. 고전 컴퓨터의 보안체계
양자 컴퓨터는 고전컴퓨터에 비해 속도 뿐 아니라 보안에 있어서도 우월한 퍼포먼스를 보일 수 있다.
좀 더 과장해서 말하자면, “이론상으로 완벽한 보안체계”를 가지고 있다.
기존 컴퓨터의 보안
간단하게 예를 들어보자. 암호학에서 주로 사용하는 비유로 ABE 상황이 있다. 이는 Alice(A)가 Bob(B)에게 비밀 메세지를 전달하고자 하는데, Eve(E)가 이를 훔쳐보려는 상황이다.
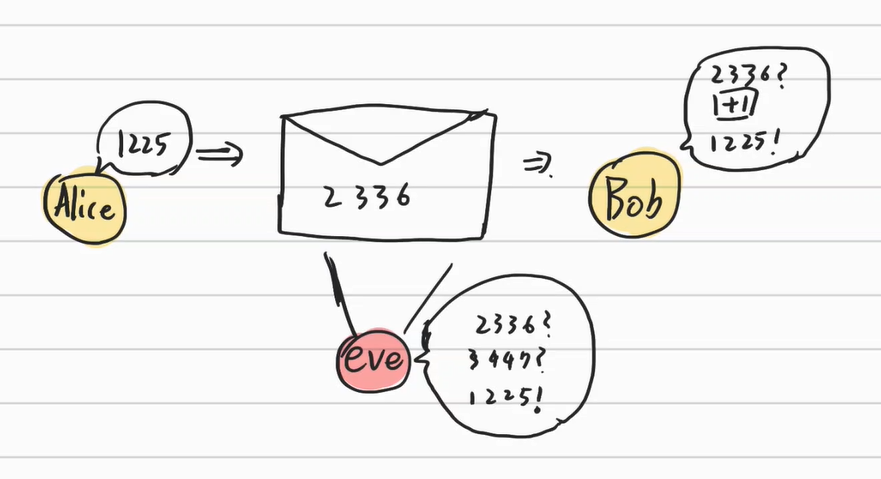
예를 들어 Alice가 1225라는 숫자를 Bob에게 보내 크리스마스를 함께 보고 싶어한다는 것을 전한다고 하자. 이때 1225라는 숫자를 편지에 적어서 보내는데, 사랑의 라이벌인 Eve가 훔쳐볼까 두렵다. 따라서 Alice는 1225라는 숫자를 Eve는 모르지만 Bob은 알 수 있는 방법으로 보내려고 한다.
보편적으로 쓰는 방법으로는 Alice가 자신의 암호를 푸는 방법을 Bob에게 미리 전달해놓는 방법이 있다. 예를 들어 1225라는 각 숫자에 1을 더해서 암호를 만든다고 하자. 이 경우 2336이라는 숫자가 편지로 전달 될 것이며 암호를 푸는 방법을 아는 Bob은 이 숫자가 1225를 의미한다는 것을 알것이고 Eve의 경우에는 모를 것이다.
이러한 방식으로 연락 당사자들만 알고 있는 암호를 쉽게 풀 수 있는 정보를 키(key)라고 부른다. 이는 현재 거의 모든 암호체계가 사용하는 방식이다.
그러나 이 방식에는 문제가 있다. Eve가 암호학을 열심히 공부 했다면 이 2336이라는 숫자가 단순히 자릿수 1을 더해서 만들어진 것임을 추론할 수 있었고, 1225를 의미함을 밝혀내 훼방을 놓을 수 있다.
RSA 암호 (Rivest/Shamir/Adlemam 암호)
따라서 쉽사리 추론하기 어려운 방식으로 암호를 만들면서도 당사자들은 쉬이 풀 수 있는 문제가 필요하다. 이러한 문제의 집합을 NP문제라고 부를 수 있다. NP문제는 알고리즘학에서 사용하는 용어로 근을 도출하는 것은 어렵지만(지수적 시간이 필요) 검산하는 것은 쉬운 문제(다항적 시간이 필요)한 문제를 의미한다. 어떠한 문제가 여기에 적합할까? 바로 소인수 분해이다.
소인수 분해는 근을 도출하는 것은 매우 어렵지만 근이 정말 소인수인지 판단하는 것은 매우 쉬운 특징을 가지고 있다. 이는 마치 암호학을 위해 만들어진 개념이라고 할 수 있을 정도로 좋은 성질이다.
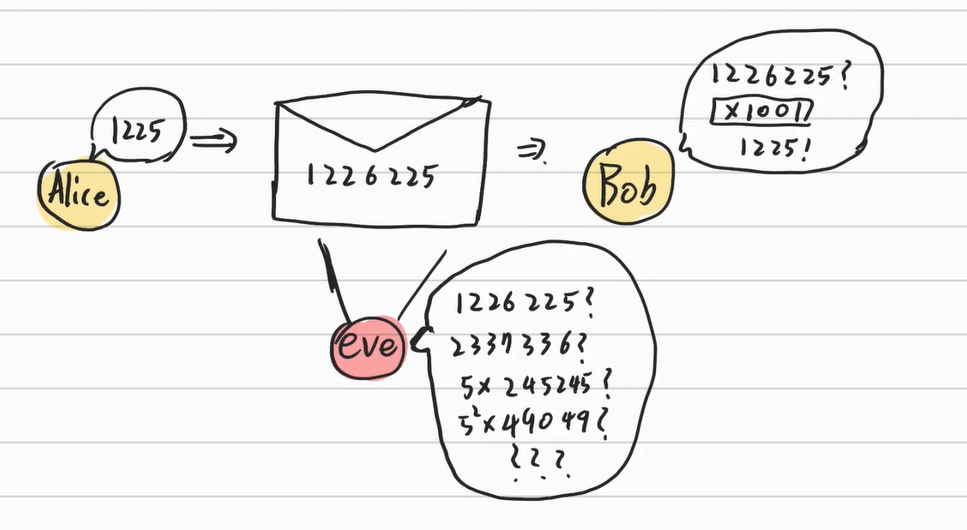
예를 들어 Alice가 1225라는 숫자를 전달할때, 밥에게 1001이라는 숫자를 미리 알려준 뒤 1225에 1001을 곱해서 전달하자. 그 다음 1225에 1001을 곱한 수인 1226225를 편지를 통해서 전달하자. 1001이라는 숫자를 알고 있는 밥은 이 숫자를 1001로 나누어 1225를 의미하는 것을 매우 쉽게 파악할 수 있다.
그러나 1001이라는 숫자를 모르는 Eve는 이 숫자를 해독하기 위해서 소인수분해를 해야한다. $5^2 7^2 1001$까지는 쉽게 알아 낼수 있으나 1001을 소인수 분해하는 것은 쉽지 않다. 따라서 Eve가 Alice와 Bob의 사랑에 훼방을 놓는 것은 거의 불가능에 가깝다.
해당 분야에 전문가는 아니라 잘 모르긴 하지만 디테일한 부분은 훨씬 복잡한 체계를 사용하며 실제로는 1226225보다 훨씬 큰 숫자를 사용할 뿐만 아니라 이 숫자 자체도 암호를 거쳐서 전달하므로 2중,3중으로 보호가 된다.
2. 양자컴퓨터의 보안체계
양자컴퓨터의 등장에 의한 RSA 암호의 무력화
그러나 이러한 소인수분해를 기반으로 한 RSA 암호는 양자컴퓨터가 등장할시 다소 무력화 된다. 양자 컴퓨터가 가장 잘할 수 있는 문제가 바로 소인수분해를 푸는 것이기 때문이다.
UCSB(UC Santa Barbara)의 John Martinis 박사의 연구결과에 따르면 2048 비트 짜리 숫자를 현재의 디지털 컴퓨터로 인수분해 하기 위해서는 $1,000,000 Trillion (100경 달러)의 예산으로 북미전체를 뒤덮는 슈퍼컴퓨터를 만든 후 10년간 10조 GW의 전력(전세계 연간 발전량이 3000GW)을 쏟아부어야 한다고 한다.
반면 양자컴퓨터를 사용할 시 1000억 달러를 투자하여 1cm 칩에 천만개의 큐빗을 담은 뒤, 16시간 동안 0.01GW의 전력을 사용하면 된다고 한다. 돈으로는 0.00001%, 전력은 0.0003%가 필요하며, 컴퓨터 크기는 비교 불가할 정도로 적게 든다.
따라서 소인수 분해를 사용하는 RSA 암호는 완전히는 아니더라도 상당부분 무력화된다. 다행히 양자 알고리즘에는 이를 대체할 만한 이론상 거의 완벽한 암호체계가 존재한다.
양자 컴퓨터의 보안 이론
양자 컴퓨터의 암호체계도 기존의 컴퓨터와 마찬가지로 키를 나눠가진다. 이때 나누어 가지는 키는 숫자 같은 것이 아니라 Qubit의 측정방향이 된다. 큐빗의 방향과 측정의 방향에 따라 큐빗의 해석이 변한다. 자세한 것은 슈테른 게를라흐 실험을 참고하자.(링크 - https://hgmin1159.github.io/quantum/quantum1/)
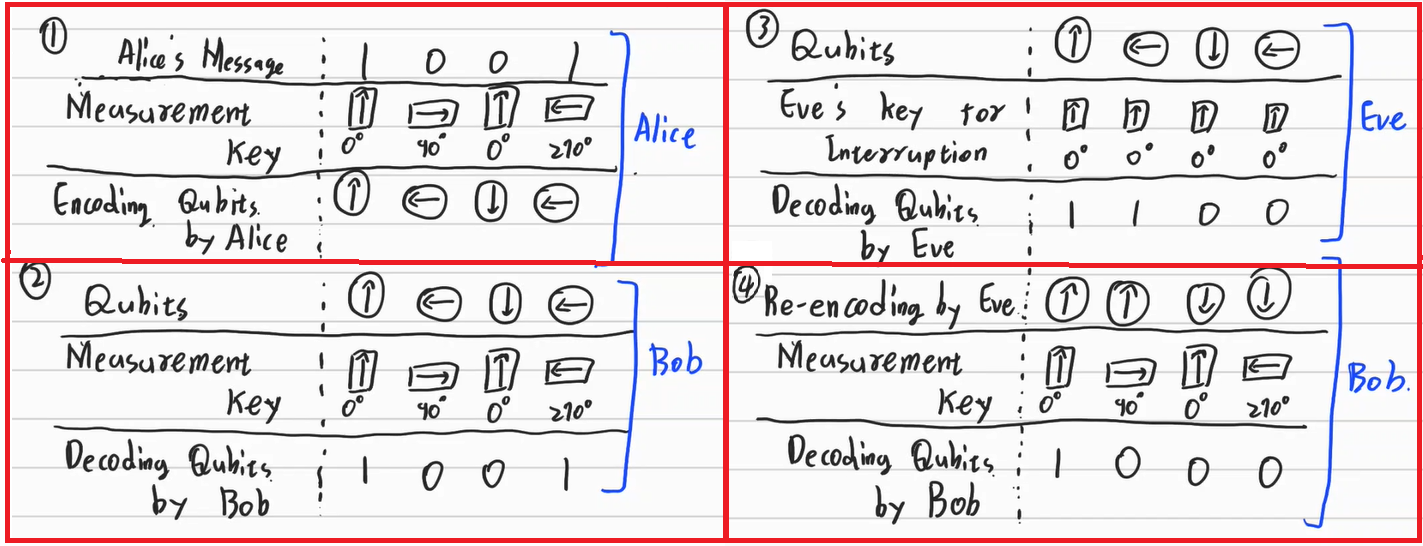
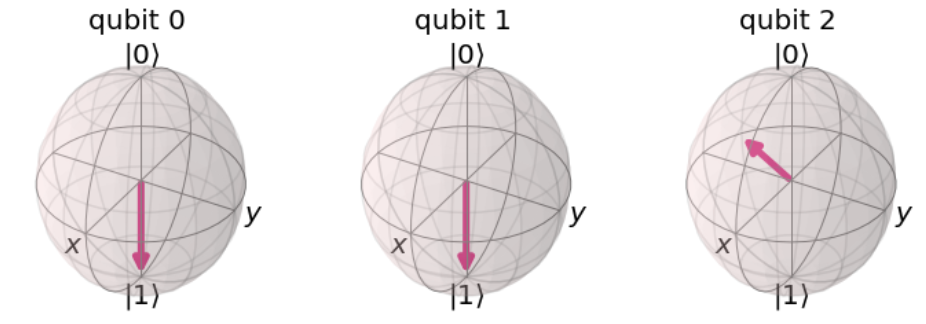
우선 Alice가 1001이라는 이진숫자를 Bob에게 전달하려 한다고 보자. 앨리스와 밥은 미리 얘기를 나누어 Qubit의 측정방향을 0도, 90도, 0도, 270도로 하기로 정해두었다. Alice는 측정방향에 맞추어 자기가 보내고 싶은 메세지를 큐빗으로 코딩한다. (1번 그림 참고)
밥은 이 큐빗을 전달 받은 후, 미리 공유한 키를 이용해 해독함으로써 엘리스가 전달하고자 한 숫자가 1001임을 알 수 있다.(2번 그림 참고)
만약 여기서 Eve가 이 메세지를 훔쳐본다고 하자. 이브는 자신이 가지고 있는 키를 이용해서 Qubit을 해석해야한다. 이 경우 이브가 0,0,0,0도의 측정방향으로 측정했다고 가정하자. 물론 이 키는 Alice의 키와 다르기 때문에 적절한 해독을 할 수 없다. (3번 그림 참고)
그러나 고전 컴퓨터의 암호체계와 다른 점은, 이 잘못된 키를 이용함으로써 Alice가 Bob에게 전달하려한 큐빗 자체의 방향이 왜곡된다는 점이다. 따라서 Eve는 측정 이전 큐빗의 상태로 되돌릴 수 없다. 따라서 Bob에게는 처음과는 다른 큐빗상태만을 전달할 수 있다는 점이다. (4번 그림 참고)
이러한 체계의 장점은 다음과 같다.
- 무수히 많은 경우의 수 - 여기서는 해독키를 단순화 해서 0,90,180,270의 4가지 케이스로 나누었지만 0~360도 사이의 무수히 많은 수가 키가 될 수 있다. 또한, 실제에서는 2차원이 아니라 3차원이므로 키의 후보는 더더욱 늘어난다. 키의 후보가 늘어난다는 것은 Eve가 암호를 풀때 고려해야하는 키의 개수가 무수히 많다는 것을 의미한다.
- 암호해독 시도가 극히 제한되어 있음 - 기존의 암호체계에서는 암호를 해독하기 위해서 여러번 시행착오를 할 수 있었다. 소인수분해를 시도하기 위해 1,2,3,5,7,11 등으로 여러번 나누어서 근을 찾을 수 있었다는 의미이다. 그러나 양자 컴퓨터에서는 한번만 시도해도 원본 정보가 날아가기 때문에 이러한 시행착오를 시도해볼 수 없다.
- 제3자의 개입 유무를 곧바로 알 수 있음 - 기본적으로 전달하고자 하는 메세지는 1001 같은 단순한 숫자가 아니라 글자 같은 것들이 숫자로 코딩된 것이다. 따라서 “안녕하세요”같은 단순한 문자도 긴 숫자로 코딩되며 이숫자가 왜곡될시 글자로 코딩이 불가할 정도로 깨지게 된다. 즉, Bob이 Alice로 부터 “디ㅏㅂㅈ뷀” 같은 문자를 받았다는 것은 Eve와 같은 제3자가 개입됐다는 사실을 바로 알 수 있다.
이러한 장점이 있어서 양자컴퓨터의 보안체계는 이론상 해킹이 불가능하다고 말할 수 있다. 물론 위의 내용은 아직 이론에 불과하며 실전용 양자컴퓨터는 개발이 되지 않았으므로 현실에 적용하기 위해서는 추가적인 알고리즘들과 장치가 필요할 것이다.
3. 양자프로토콜
아직 위에서 제시한 방식은 현존하는 양자컴퓨터 시스템에 완전히 녹여내지는 못한 방식이다. 두 양자컴퓨터에서 양자정보를 전달하는 실험자체가 아직은 힘들기 때문이다.
따라서 이를 좀 더 현실적으로 접근하기 위해서 양자정보의 전달체계 이론이 선행해서 만들어 졌는데, 이것이 바로 Superdense Code와 Quantum Teleportation이다.
Superdense Code
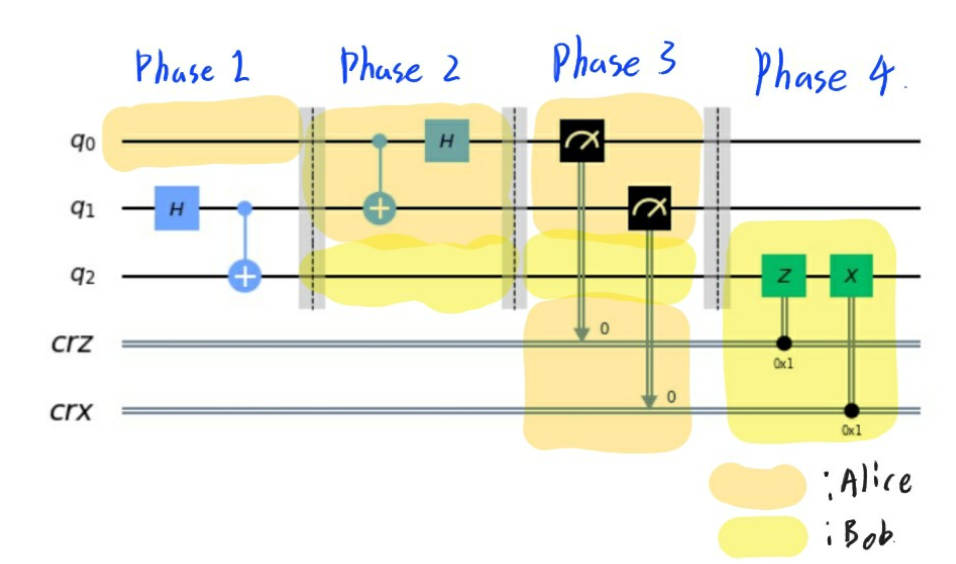
Superdense Code는 큐빗 한개를 전달함으로써 비트 두개를 전달하는 알고리즘이다.
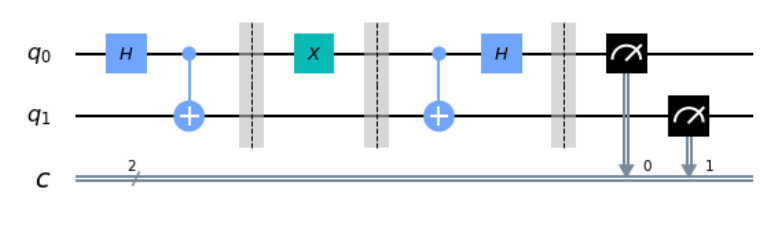
Superdense Code의 기본적인 회로는 위와 같다.
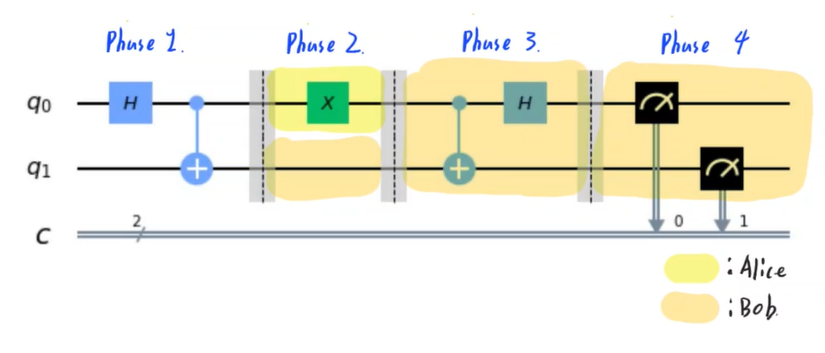
Phase 1.
-
처음 들어가는 인풋 $\ket{q_0q_1}$은 $\ket{00}$이다. 이 큐빗을 Bell’s Circuit에 통과시켜서 완전히 얽혀있는 큐빗을 만든다.
$\ket{00} \Rightarrow \frac{1}{\sqrt 2}(\ket{0}+\ket{1})\otimes\ket{0} \Rightarrow \frac{1}{\sqrt{2}}(\ket{00}+\ket{11})$
-
그리고 이 두 큐빗을 Alice와 Bob이 각각 나누어 가진다.
Phase 2.
- Alice는 이 큐빗 하나를 조작함으로써 전달될 정보를 정할 수 있다.
하나의 큐빗으로 표현할 수 있는 정보는 2비트이며 00,01,10,11 중 하나가 된다. 통과시키는 게이트에 따라 전달되는 비트는 아래와 같다.
| 게이트 | 결과물 비트 |
|---|---|
| I | 00 |
| X | 01 |
| Z | 10 |
| Z - X | 11 |
만약 X를 통과시키면 규빗은 다음과 같이 변한다.
$ \frac{1}{\sqrt{2}}(\ket{00}+\ket{11}) \Rightarrow \frac{1}{\sqrt{2}}(\ket{10}+\ket{01})$
Phase 3.
- Bob은 Alice가 조작한 큐빗을 넘겨 받아서 자신의 큐빗과 함께 Inverse Bell’s Qubit을 돌린다. 그 경우 큐빗은 아래와 같이 변한다.
$\frac{1}{\sqrt{2}}(\ket{10}+\ket{01}) \Rightarrow \frac{1}{\sqrt{2}}(\ket{11}+\ket{01}) \Rightarrow \ket{01}$
Phase 4.
- 이런 처리를 거친 큐빗을 측정하면 100% 확률로 01이 측정된다.
이 서킷을 이용하면 2N개의 비트를 전달하기 위해서 N개의 큐빗만 전달하면 된다.
실제로 한번 해보자.
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
circ = QuantumCircuit(2,2)
circ.h(0)
circ.cx(0,1)
circ.barrier()
circ.x(0)
circ.barrier()
circ.cx(0,1)
circ.h(0)
circ.barrier()
circ.measure([0,1],[0,1])
circ.draw(output='mpl',justify='none')
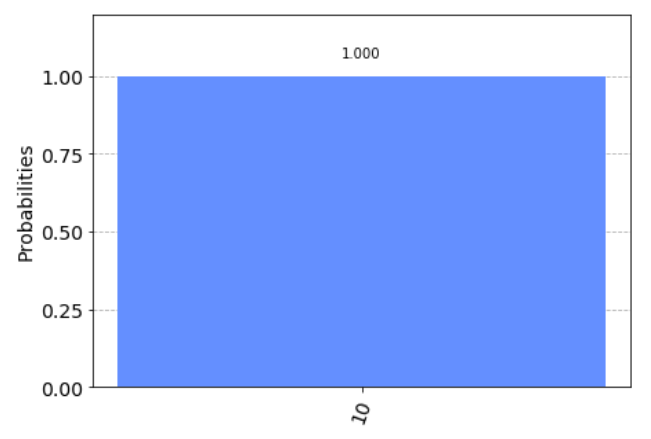
서킷은 위와 같다. 이 회로를 카즘 시뮬레이터에 돌리면 다음과 같은 결과가 나온다.
job_result = execute(circ, Aer.get_backend('qasm_simulator'))
plot_histogram(job_result.result().get_counts(circ))
100%확률로 10이 반환된것을 확인할 수 있다.
Quantum Teleportation
Quantum Teleportation은 Alice가 가지고 있는 큐빗을 Bob에게로 옮기는 기술이다. 이는 다음과 같은 회로를 가진다.
Phase 1
- $\ket{q_0}$는 Alice가 전달하고자 하는 큐빗이다. 이를 다음과 같이 표현하자. $\ket{q_0} = a\ket{0}+b\ket{1}$
- 이 큐빗은 가지고 있고 Alice와 Bob이 미리 Bell’s Circuit을 거친 두 큐빗을 나누어 가진다. 즉, 아래와 같다.
$\ket{q_0}\otimes\ket{00} \Rightarrow \ket{q_0}\otimes\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{0} \Rightarrow \ket{q_0}\otimes\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})$
Phase 2
- Alice는 얻어가진 큐빗과 전달할 큐빗을 Inverse-Bells-Circuit에 통과 시킨다. 이 경우 큐빗은 아래와 같이 변한다.
$\ket{q_0}\otimes\frac{1}{\sqrt{2}}(\ket{00}+\ket{11}) \Rightarrow \frac{a}{\sqrt{2}}\ket{0}\otimes(\ket{00}+\ket{11})+\frac{b}{\sqrt{2}}\ket{1}\otimes(\ket{11}+\ket{01}) \Rightarrow \frac{1}{2}[\ket{00}(a\ket{0}+b\ket{1})+\ket{01}(b\ket{0}+a\ket{1})+\ket{10}(a\ket{0}-b\ket{1})+\ket{11}(-b\ket{0}+a\ket{1})]$
- 여기서 2번째에서 3번째로 넘어가는 Hadamard 게이트의 경우 첫번째 큐빗을 다음과 같이 바꿔준다. 이를 정리해주면 위와 같은 결과가 나온다.
$\ket{0} \rightarrow \frac{1}{\sqrt 2}(\ket{0}+\ket{1}),\ket{1} \rightarrow \frac{1}{\sqrt 2}(\ket{0}-\ket{1})$
Phase 3
-
Alice는 이 큐빗을 측정한 후 결과를 밥에게 보낸다. 밥은 받은 비트가 00 일시 I를, 01일시 x를, 10일시 z를, 11일시 z 이후 x 게이트를 $\ket{q_2}$ 적용한다.
- 즉, 00일시 Bob이 가진 큐빗은 $(a\ket{0}+b\ket{1})$이므로 그대로 두고, 01일시 Bob이 가진 큐빗은 $(b\ket{0}+a\ket{1})$이므로 X게이트를 적용해준다.
- 이러한 과정을 거치면 밥은 자신의 큐빗을 $\ket{q_0} = a\ket{0}+b\ket{1}$로 바꿀 수 있다.
실제로 한번 해보자.
우선 해당 회로에는 c_if 메서드가 필요한데 이를 이용하려면 처음 Circuit을 정해줄 때 Register를 이용해서 넣어야 한다. 즉 다음과 같다.
from qiskit import QuantumRegister, ClassicalRegister
qr = QuantumRegister(3, name="q")
crz = ClassicalRegister(1, name="crz")
crx = ClassicalRegister(1, name="crx")
그 다음으로 임의의 상태를 가진 게이트를 만들어주자. 키스킷 내부의 교육용 함수를 사용하면 된다.
from qiskit_textbook.tools import random_state
from qiskit.extensions import Initialize
from qiskit.visualization import plot_bloch_multivector
psi = random_state(1)
init_gate = Initialize(psi)
init_gate.label = "init"
plot_bloch_multivector(psi)
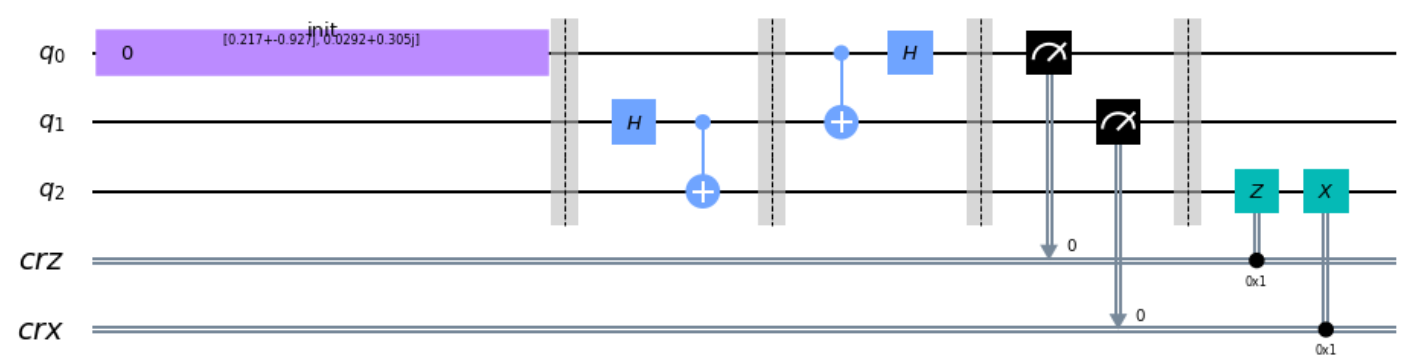
이제 이를 활용하여 회로를 짜주자. 회로는 다음과 같다.
circ = QuantumCircuit(qr,crz,crx)
circ.append(init_gate, [0])
circ.barrier()
circ.h(1)
circ.cx(1,2)
circ.barrier()
circ.cx(0,1)
circ.h(0)
circ.barrier()
circ.measure(0,crz)
circ.measure(1,crx)
circ.barrier()
circ.z(qr[2]).c_if(crz,1)
circ.x(qr[2]).c_if(crx,1)
circ.draw(output='mpl',justify='none')
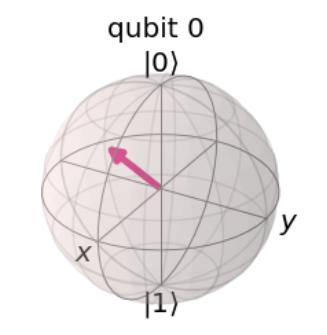
다음으로 이 큐빗의 상태를 측정없이 보려면 카즘시뮬레이터가 아닌 Statevector 시뮬레이터가 필요하다. 또한 큐빗 하나를 완벽하게 시각화하기 위해서 Bloch Sphere시각화를 사용하자.
backend= Aer.get_backend('statevector_simulator')
result = execute(circ, backend).result()
psi = result.get_statevector()
plot_bloch_multivector(psi)
세번째 큐빗이 처음 랜덤한것과 완전히 똑같은 것을 확인할 수 있다.
여기까지 양자 컴퓨터의 보안체계에 대해서 살펴보았다. 두 회로는 사실 실전에서 쓰인적이 없다. 현재는 두 양자컴퓨터 간에서 양자를 전달하는 행위를 하기에는 기술이 부족하기 때문이다. 그래도 이 두가지 회로는 기본적인 회로가 어떻게 돌아가는지 알 수 있으며 차후에도 연구가치가 있는 회로라고 할 수 있다.
Sutor, R. (2019). Dancing With Qubits. Birmingham,UK:Packt
Bernhardt, C. (2019). Quantum computing for everyone. Boston, Massachusetts:The MIT Press