문제의 가정은 다음과 같다.
$y_i = X_i \beta + \epsilon_i \ , \ i=1,2,…,N$
where $y_i \in R , X_i \in R^p , \beta \in R^p$
and $\epsilon_i \sim N(0,\sigma^2)$$D= (X_i,y_i)^N_{i=1} , z=(\beta,\sigma^2) ,\kappa,a,b$는 상수
Prior
$\beta \sim N(0,\kappa I)$
$\sigma^2 \sim IG(a,b)$
이에 대해서 두가지 접근으로 VI(;Variational Inference)를 시행해야 한다. 첫번째는 z에 tractable한 분포를 할당하고 시작하는 방법이며, 두번째는 ELBO를 최대화 시키는 미분값 공식을 바로 사용하는 것이다.
1. Tractable 분포 할당 접근
이 경우 $\beta$와 $\sigma^2$를 각각 다음과 같이 할당해주자
$\beta \sim N(\mu,\tau I)$
$\sigma^2 \sim IG(c,d)$
a. ELBO 구하기
위와 같은 설정하에서 ELBO를 구하는 방법은 다음과 같다.
ELBO $= E_q(log \ p(z,D)-log \ q(z))$
$=E_q(log \ p(D \mid z)+log \ p(z) - log \ q(z))$
$= E_q(\sum log \ N(y_i ; X_i \beta,\sigma^2)+log \ N(\beta ; 0, \kappa I)IG(\sigma^2 ;a,b)-log \ N(\beta ; \mu,\tau I)IG(\sigma^2;c,d))$
위의 결과물을 순서대로 다음과 같이 설정해주자
$=E_q(A+B-C)$
그렇다면 파트별로 다음과 같이 풀린다.
$E_q(A) = E_q(\sum log \ N(y_i ; X_i \beta,\sigma^2))$
$= E_q(\sum log \ \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2\sigma^2}(y_i-X_i\beta)^2))$
$=E_q(n \ ln(\frac{1}{\sqrt{2\pi}})+\frac{n}{2}ln(\frac{1}{\sigma^2})-\frac{1}{2\sigma^2}(y-X\beta)^t(y-X\beta))$
$= n \ ln\frac{1}{\sqrt{2\pi}} - \frac{n}{2}<ln \ \sigma^2>- <\frac{1}{2\sigma^2}><(y-X\beta)^t(y-X\beta)>$
$E_q(B) = E_q(log \ N(\beta ; 0, \kappa I)IG(\sigma^2 ;a,b))$
$=E_q(ln \ \frac{1}{2\pi}^{p/2}\frac{1}{\kappa}^{p/2}exp(-\frac{1}{2\kappa}\beta^t\beta)\frac{b^a}{\gamma(a)}\frac{1}{\sigma^2}^{a+1}exp(-\frac{b}{\sigma^2}))$
$=E_q(p \ ln \frac{1}{\sqrt{2\pi}}+\frac{p}{2}ln \frac{1}{\kappa} + ln \frac{b^a}{\gamma(a)}+(a+1)ln \frac{1}{\sigma^2} -\frac{1}{2\kappa}\beta^t\beta-\frac{b}{\sigma^2})$
$=p \ ln\frac{1}{\sqrt{2\pi}}+\frac{p}{2}ln \frac{1}{\kappa}+ln\frac{b^a}{\gamma(a)}-(a+1)<ln \ \sigma^2> - \frac{1}{2\kappa}<\beta^t\beta>-b<\frac{1}{\sigma^2}>$
$E_q(C) = E_q(log \ N(\beta ; \mu,\tau I)IG(\sigma^2;c,d))$
$=E_q(ln \ \frac{1}{2\pi}^{p/2}\frac{1}{\tau}^{p/2}exp(-\frac{1}{2\tau}(\beta-\mu)^t(\beta-\mu))\frac{d^c}{\gamma(c)}\frac{1}{\sigma^2}^{c+1}exp(-\frac{d}{\sigma^2}))$
$=E_q(\frac{p}{2} ln \frac{1}{2\pi} - \frac{p}{2} ln \ \tau + ln\frac{d^c}{\gamma(c)}-(c+1)ln \ \sigma^2-\frac{1}{2\tau}(\beta-\mu)^t(\beta-\mu)-\frac{d}{\sigma^2})$
$=\frac{p}{2} ln \frac{1}{2\pi} - \frac{p}{2} ln \ \tau + ln\frac{d^c}{\gamma(c)} -(c+1)<ln \ \sigma^2> -\frac{1}{2\tau}<(\beta-\mu)^t(\beta-\mu)>-d<\frac{1}{\sigma^2}>$
위 식에서 기댓값을 구해야 하는 부분을 각각 구하면 다음과 같다.
-
$<ln \ \sigma^2> = ln(d) - \psi(c) $ (IG 분포의 성질)
where $\psi(c) = \frac{\gamma’(c)}{\gamma(c)}$(digamma function) -
$<\frac{1}{\sigma^2}>=\frac{c}{d}$
-
$<\beta> = \mu $
-
$<(\beta-\mu)^t(\beta-\mu)> = <tr((\beta-\mu)(\beta-\mu)^t)>=tr(\tau I)=p\tau$
$=<\beta^t\beta -2 \mu^t \beta +\mu^t\mu>=<\beta^t\beta>-\mu^t\mu$
-
$<\beta^t\beta>=p\tau+\mu^t\mu$
-
$<(y-X\beta)^t(y-X\beta)>=y^ty-2y^tX<\beta>+<\beta^tX^tX\beta>$
$=y^ty-2y^tX\mu+tr(X^tX)\tau+\mu^t X^tX \mu$ $\equiv SSE_{\beta = \beta^{t}}$
(${E(x^tAx)=tr(A\Sigma)+\mu^tA\mu}$ 공식 사용)
이를 이용해서 각각의 Expectation을 구해보자
b. Expectation 구하기
$E_q(A)= n \ ln\frac{1}{\sqrt{2\pi}} - \frac{n}{2}<ln \ \sigma^2>- <\frac{1}{2\sigma^2}><(y-X\beta)^t(y-X\beta)>$
$= n \ln \frac{1}{\sqrt{2\pi}}-\frac{n}{2}(ln(d)-\psi(c))-\frac{c}{2d}y^ty+\frac{c}{2d}2y^tX\mu-\frac{c}{2d}tr(X^tX)\tau-\frac{c}{2d}\mu^t X^tX \mu$
$E_q(B)=p \ ln\frac{1}{\sqrt{2\pi}}+\frac{p}{2}ln \frac{1}{\kappa}+ln\frac{b^a}{\gamma(a)}-(a+1)<ln \ \sigma^2> - \frac{1}{2\kappa}<\beta^t\beta>-b<\frac{1}{\sigma^2}>$ $=p \ ln\frac{1}{\sqrt{2\pi}}+\frac{p}{2}ln \frac{1}{\kappa}+ln\frac{b^a}{\gamma(a)}-(a+1)(ln(d)-\psi(c)) - \frac{1}{2\kappa}(p\tau+\mu^t\mu)-b(\frac{c}{d})$
$E_q(C)=\frac{p}{2} ln \frac{1}{2\pi} - \frac{p}{2} ln \ \tau + ln\frac{d^c}{\gamma(c)} -(c+1)<ln \ \sigma^2> -\frac{1}{2\tau}<(\beta-\mu)^t(\beta-\mu)>-d<\frac{1}{\sigma^2}>$ $=\frac{p}{2} ln \frac{1}{2\pi} - \frac{p}{2} ln \ \tau + ln\frac{d^c}{\gamma(c)} -(c+1)(ln(d)-\psi(c)) -\frac{p}{2}-c$
$Q = E_q(A)+E_q(B)-E_q(C)$
c.Maximization 하기
위의 Q 함수에 $c>0 ,d>0 , \tau >0$이라는 제약을 함께 달아주어야 한다. 그렇다면 Inequality constrained optimization problem으로 변형되며 KKT condition이라는 것을 풀어주면 된다고 한다. 이 문제에 대한 KKT Condition은 다음과 같다.
$L = Q + \lambda_1 c + \lambda_2 d + \lambda_3 \tau$에 대해서
- $\frac{\delta L}{\delta \theta} = 0$ {$\theta = (c,d,\tau)$}
- $\lambda_i \geq 0$
- $\lambda_1 c =0 , \lambda_2 d=0 , \lambda_3 \tau =0$
위를 만족하는 $\theta, \lambda_i$를 구하면 제약하에서 Q를 최적화하는 공식을 얻어낼 수 있다.
- $\mu$의 경우
$\frac{d}{d\mu}L \propto \frac{d}{d\mu}(\frac{c}{2d}y^tX\mu-\frac{c}{2d}\mu^tX^tX\mu-\frac{1}{2\kappa}\mu^t\mu)$
$=\frac{c}{d}X^ty-\frac{c}{d}X^tX\mu-\frac{1}{\kappa}\mu = 0$
$\mu^{(t+1)} = \frac{c}{d}(\frac{c}{d}X^tX+\frac{1}{\kappa}I)^{-1}X^ty$
- $\tau$의 경우
$\frac{d}{d\tau}L \propto \frac{d}{d\tau}(-\frac{c}{2d}tr(X^tX)\tau-\frac{p}{2\kappa}\tau+\frac{p}{2}ln \ \tau + \lambda_3 \tau)$
$= -\frac{c}{2d}tr(X^tX)-\frac{p}{2\kappa}+\frac{p}{2\tau} + \lambda_3=0$
$\lambda_3 \tau =0$
두식을 연립해서 풀면
$\tau^{(t+1)}=\frac{dp}{c \ tr(X^tX)}+\kappa , \lambda_3 =0$
$\tau^{(t+1)}=\frac{dp \kappa}{c \ tr(X^tX) \kappa +dp}, \lambda_3 =0$
- c의 경우
$\frac{d}{dc}L \propto \frac{d}{dc}((a+\frac{n}{2}+1)\psi(c)-\frac{c}{2d}SSE_{\beta=\beta^t}-\frac{bc}{d}-ln \frac{d^c}{\gamma(c)}+(c+1)(ln(d)-\psi(c))+c + \lambda_1 c)$
$= (a+\frac{n}{2}-c)\psi’(c) +ln(d)-ln \ d +1 - \frac{b}{d}-\frac{1}{2d}SSE_{\beta=\beta^{t}} + \lambda_1 = 0$
$\lambda_1 c =0 $
- d의 경우
$\frac{\delta}{\delta d}L \propto \frac{\delta}{\delta d}(-\frac{n}{2}ln(d)-\frac{c}{2d}SSE_{\beta=\beta^{t}}-(a+1)ln(d)-b\frac{c}{d}-c \ ln \ d +(c+1)ln(d) + \lambda_2 d)$
$=-(a+\frac{n}{2}-c)\frac{1}{d}+\frac{c}{2d^2}SSE_{\beta=\beta^t}+\frac{bc}{d^2}-\frac{c}{d} + \lambda_2=0$
$\lambda_2 d =0$
c식과 d식, $\lambda$ 조건을 연립하여 풀어보면 $c = a+\frac{n}{2} , d=b+\frac{1}{2}SSE_{\beta=\beta^t} , \lambda_1 =0 , \lambda_2 =0 $일시 모두 0이 된다.
c식과 d식, $\lambda$ 조건을 연립하여 풀어보면 $c = a+\frac{n}{2} , d=b+\frac{1}{2}SSE_{\beta=\beta^t} , \lambda_1 =0 , \lambda_2 =0 $일시 모두 0이 된다.
d. 코딩 하기
우선 데이터를 불러와주자 $1000 \times 4$의 데이터를 사용했다.
data = read.csv("trainset.csv")
X = as.matrix(data[,3:dim(data)[2]])
y = as.matrix(data[,2])
그 다음 알고리즘의 상수항 부분들을 설정해주자
iter=10000
n=dim(X)[1]
p=dim(X)[2]
a=1
b=1
kappa = 1
다음으로 알고리즘의 초기값을 설정해주자
mu_temp = t(t(as.vector(c(1000,1000,1000,1000))))
tau_temp = 0.01
c_temp=10
d_temp=10
elbo1_temp = 0
위에서 구한 식에 따르면 이터레이션이 진행됨에 따라 변하지 않는 상수부들이 있다. 이 부분들을 이터레이션 밖에서 미리 계산해서 효율성을 높여주도록 하자
yty = t(y)%*%y
xtx = t(X)%*%(X)
tr = sum(diag(xtx))
xty = t(X)%*%y
최적화 정도를 확인하기 위해서 ELBO를 계산하는 함수를 짜보자. 1번 문제에서 ELBO는 $n,p,\mu,\tau,c,d$에만 의존한다 따라서 이들을 인수로 받아주는 함수를 짜면 될것이다.
거기에 더해, c가 500 가까운 수치가 되는데 컴퓨터에게 $log(\gamma(500))$을 계산하게 하면 $\gamma(500)$부터 계산하는데 이는 컴퓨터에서 계산할 수 있는 유효숫자를 넘어서는 수이다. 이러한 문제 때문에 r에는 lgamma 라는 log-gamma를 계산해주는 함수가 따로 있다. 이를 사용해주자
elbo1 = function(mu,tau,c,d){
A = n*log(1/sqrt(2*pi)) - n/2*(log(d)-digamma(c))-c/2/d*(yty-2*t(t(mu)%*%xty)+tr*tau+t(mu)%*%xtx%*%mu)
B = p*log(1/sqrt(2*pi))+p/2*log(1/kappa)+a*log(b)-lgamma(a)-(a+1)*(log(d)-digamma(c))-1/2/kappa*(p*tau+t(mu)%*%mu)-b*c/d
C = p/2*log(1/2/pi)-p/2*log(tau)+c*log(d)-lgamma(c)-(c+1)*(log(d)-digamma(c))-p/2-c
return(A+B-C)
}
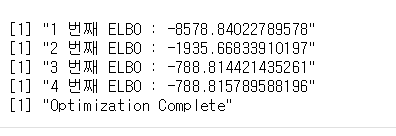
다음으로 본격적인 최적화 이터레이션 폼을 짜주자. 이터레이션은 1만번으로 설정했지만 최적화에 따라서 ELBO의 변화율이 1%아래로 떨어지면 Ealry Stopping을 할 수 있도록 함수를 짜주었다.
for (i in 1:iter){
exp_beta = yty - 2 * t(xty) %*% mu_temp + t(mu_temp) %*% xtx %*% mu_temp + tr*tau_temp
c_temp = a+n/2
d_temp = b+exp_beta/2
exp_sigma = as.numeric(c_temp/d_temp)
mu_temp = exp_sigma*solve(exp_sigma* xtx+diag(p)/kappa)%*%xty
tau_temp = (c_temp*sum(diag(xtx))/d_temp*p+1/kappa)^(-1)
exp_beta = yty - 2 * t(xty) %*% mu_temp + t(mu_temp) %*% xtx %*% mu_temp + tr*tau_temp
print(paste(i,"번째 ELBO :" , elbo1(mu_temp,tau_temp,c_temp,d_temp)))
if(abs(elbo1_temp-elbo1(mu_temp,tau_temp,c_temp,d_temp)) < abs(elbo1_temp)*0.01 ){
print("Optimization Complete")
break
}
elbo1_temp = elbo1(mu_temp,tau_temp,c_temp,d_temp)
}
2. MFVI 최적화 공식 사용하기
Mean Field Assumtion 하에서 ELBO를 최적화 하는 공식은 이미 도출 되어 있다. 그는 아래와 같다.
$q_i(z_i) \propto exp(E_{q_{-i}}(log \ p(z_i \mid z_{-i},D)))$
이를 이 문제에 적용하면 다음과 같다.
$q(\beta) \propto exp(E_{q(\sigma^2)}[log \ p(\beta \mid \sigma^2 ,D)])$
$q(\sigma^2) \propto exp(E_{q(\beta)}[log \ p(\sigma^2 \mid \beta ,D)])$
a. Variational 구하기
이제 이를 구하기 위해 Joint Distribution을 구하자
$p(z,D) = p(D \mid z) p(z)$
$= \prod_i N(y_i ; X\beta,\sigma^2) N(\beta;0,\kappa I) IG(\sigma^2 ; a,b)$
$= (\frac{1}{2\pi})^{\frac{n}{2}}(\frac{1}{\sigma^2})^{\frac{n}{2}}exp(-\frac{1}{2\sigma^2}(y-X\beta)^t(y-X\beta))$
$\times (\frac{1}{2\pi})^{\frac{p}{2}}(\frac{1}{\kappa})^{\frac{p}{2}}exp(-\frac{1}{2\kappa}\beta^t\beta)\frac{b^a}{\gamma(a)}exp(-\frac{b}{\sigma^2})$
$p(\beta \mid \sigma^2 ,D ) \propto exp(-\frac{1}{2\sigma^2}(\beta^tX^tX\beta-2\beta^tX^ty)-\frac{1}{2\kappa}\beta^t\beta)$
$= exp(-\frac{1}{2}(\beta^t(\frac{1}{2\sigma^2}X^tX+\frac{1}{\kappa}I)\beta-\frac{2}{\sigma^2}y^tX\beta))$
이는 다중 정규분포의 커널과 동일한 꼴이다. 따라서 결과물을 적절히 정리하면 다음과 같이 유도할 수 있다.
$\beta \mid \sigma^2 ,D \sim N(\frac{1}{\sigma^2}(\frac{1}{\sigma^2} X^tX + \frac{1}{\kappa}I)^{-1}X^ty,(\frac{1}{\sigma^2} X^tX + \frac{1}{\kappa}I)^{-1}) \equiv N(\mu , \Sigma)$
$p(\sigma^2 \mid \beta ,D) \propto (\frac{1}{\sigma^2})^{(a+\frac{n}{2}+1)}exp(-\frac{b}{\sigma^2}-\frac{1}{2\sigma^2}(y-X\beta)^t(y-X\beta))$
$= (\frac{1}{\sigma^2})^{(a+\frac{n}{2}+1)}exp(-\frac{1}{2\sigma^2}(2b+(y-X\beta)^t(y-X\beta)))$
이는 Inverse Gamma 분포의 커널과 동일한 꼴이다. 따라서 결과물을 적절히 정리하면 다음과 같이 유도할 수 있다.
$\sigma^2 \sim IG(a+\frac{n}{2},b+\frac{1}{2}(y-X\beta)^t(y-X\beta)) \equiv IG(c,d)$
B. ELBO 구하기
ELBO를 구하기 위해서 1번 문제에서 썻던 식을 써주자
$ELBO=E_q(log \ p(D \mid z)+log \ p(z) - log \ q(z))$
$\equiv E_q(A)+E_q(B)-E_q(C)$
$E_q(A)= n \ln \frac{1}{\sqrt{2\pi}}-\frac{n}{2}(ln(d)-\psi(c))-\frac{c}{2d}y^ty+\frac{c}{2d}2y^tX\mu-\frac{c}{2d}tr(X^tX\Sigma)-\frac{c}{2d}\mu^t X^tX \mu $
$E_q(B)=p \ ln\frac{1}{\sqrt{2\pi}}+\frac{p}{2}ln \frac{1}{\kappa}+ln\frac{b^a}{\gamma(a)}-(a+1)(ln(d)-\psi(c)) - \frac{1}{2\kappa}(tr(\Sigma)+\mu^t\mu)-b(\frac{c}{d}) $
그리고 사실 C 부분은 Entropy의 정의와 일치하기 때문에 standard한 분포에서는 공식을 그대로 써줄 수 있다.
Multinormal의 Entropy 공식 $= \frac{1}{2}log(det(2\pi e \Sigma))$
Inverse-Gamma의 Entropy 공식 $= c+ log(d * \Gamma(c))-(1+c)\psi(c)$
C. Expectation 취하고 Maximization 해주기
이렇게 구한 조건부 분포들을 공식에 적용하면 다음과 같다.
$q(\beta) \propto E_{q(\sigma^2)}(p(\beta \mid \sigma^2 ,D))$
$\sim N(<\frac{1}{\sigma^2}>(<\frac{1}{\sigma^2}> X^tX + \frac{1}{\kappa}I)^{-1}X^ty,(<\frac{1}{\sigma^2}> X^tX + \frac{1}{\kappa}I)^{-1})$
$q(\sigma^2) \propto E_{q(\beta)}(p(\sigma^2 \mid \beta ,D))$
$\sim IG(a+\frac{n}{2},b+<\frac{1}{2}(y-X\beta)^t(y-X\beta)>)$
이때 기댓값들은 위에서 구한 것과 똑같이 써주자
d. 코딩하기
코딩 부분은 1번 문제와 대동소이하다. 1번에서는 베타의 공분산을 스칼라*Identity Matirx로 표현했으나 이번에는 공분산 행렬을 그대로 써주면 된다.
데이터를 불러오고
data = read.csv("trainset.csv")
X = as.matrix(data[,3:dim(data)[2]])
y = as.matrix(data[,2])
초기항과 상수항, 이터레이션 바깥부분을 미리 설정해주고
iter=10000
n=dim(X)[1]
p=dim(X)[2]
beta_m_temp = c(1000,1000,1000,1000)
beta_var_temp = diag(0.01,p)
sigma_a_temp=1
sigma_b_temp=1
elbo2_temp = 0
a=1
b=1
kappa = 1
yty = t(y)%*%y
xtx = t(X)%*%(X)
xty = t(X)%*%y
ELBO 함수를 짜주고
elbo2 = function(mu,sigma,c,d){
A = n*log(1/sqrt(2*pi)) - n/2*(log(d)-digamma(c))-c/2/d*(yty-2*t(t(mu)%*%xty)+sum(diag(t(X)%*%X%*%sigma))+t(mu)%*%xtx%*%mu)
B = p*log(1/sqrt(2*pi))+p/2*log(1/kappa)+a*log(b)-lgamma(a)-(a+1)*(log(d)-digamma(c))-1/2/kappa*(sum(diag(sigma))+t(mu)%*%mu)-b*c/d
C = 1/2*log(det(2*pi*sigma*exp(1))) + c+ log(d)+lgamma(c)-(1+c)*digamma(c)
return(A+B-C)
}
이터레이션을 돌리면 된다.
for (i in 1:iter){
exp_beta = yty - 2 * t(xty) %*% beta_m_temp + t(beta_m_temp) %*% xtx %*% beta_m_temp + sum(diag(xtx%*%beta_var_temp))
sigma_a_temp = a+n/2
sigma_b_temp = b+exp_beta/2
exp_sigma = as.numeric(sigma_a_temp/sigma_b_temp)
beta_m_temp = exp_sigma*solve(exp_sigma* xtx+diag(p)/kappa)%*%xty
beta_var_temp = solve(exp_sigma* xtx+diag(p)/kappa)
print(paste(i,"번째 ELBO :" , elbo2(beta_m_temp,beta_var_temp ,sigma_a_temp,sigma_b_temp )))
if(abs(elbo2_temp-elbo2(beta_m_temp,beta_var_temp ,sigma_a_temp,sigma_b_temp )) < abs(elbo2_temp)*0.01 ){
print("Optimization Complete")
break
}
elbo2_temp =elbo2(beta_m_temp,beta_var_temp ,sigma_a_temp,sigma_b_temp )
}
3. 결과물 비교
두 식의 결과물을 정리하면 아래와 같다.
result_beta = cbind(mu_temp,beta_m_temp,t(t(as.vector(lm(y~X[,2:4])$coefficients))))
dimnames(result_beta) = list(c("x1","x2","x3","x4") , c("첫번째 방법","두번째 방법","Frequantists 추정치"))
result_sigma = cbind( d_temp/c_temp,sigma_b_temp/sigma_a_temp)
dimnames(result_sigma) = list(c("분산"),c("첫번째 방법","두번째 방법"))
print("Beta 기댓값 비교")
print(result_beta)
print("분산 추정량 비교")
print(result_sigma)
test = read.csv("testset.csv")
x_test = as.matrix(test[,3:6])
y_test = as.matrix(test[,2])
print(paste("첫번째 접근법의 L2 기준:",sum((y_test - x_test %*% t(t(as.vector(result_beta[,1]))))^2) + result_sigma[1] * dim(X)[1]))
print(paste("두번째 접근법의 L2 기준:",sum((y_test - x_test %*% t(t(as.vector(result_beta[,2]))))^2) + result_sigma[2] * dim(X)[1]))
둘의 점수는 대동소이 하다.
첫번째 접근법은 목표 분포를 가정한 후 풀어나간 방식이다. 그러나 $\beta$에 대한 분포 가정에서 베타 끼리 독립가정을 했기 때문에 어쩌면 결과값에 왜곡이 있을 수 있다.
두번째 접근법을 취했을 때 공식을 취해서 넣어주니 standard한 분포가 도출되었다. 그러나 만약 도출이 되지 않는다면 그 때 첫번째 접근법을 취해주고 근사 분포를 찾아내는 것이 적절한 방법이라고 말 할 수 있다.