$\def\ket#1{\mid #1\rangle}$
Introduction to Quantum Machine Learning
수정예정(오류있음)
Quantum Machine Learning
양자 컴퓨터를 이용하면 생물학,화학,금융,수학 등 많은 분야의 어려운 문제들을 풀어낼 수 있다. 이는 데이터 사이언스 분야 또한 마찬가지이다. $\def\ket#1{\mid #1 \rangle}$
예컨데, 275개의 큐빗을 이용하면 총 $2^{275} \approx 10^{85}$개 만큼의 비트정보를 표현할 수 있는데, 이는 우리가 관측가능한 우주의 원자의 개수와 일치한다. 즉, 오직 275개의 큐빗을 이용해서 우주를 표현할 수 있다는 것이다.
따라서 이론상으로 양자컴퓨터는 데이터를 매우 효율적으로 다룰 수 있다. 그러나 현재는 아직 관련 연구가 진행 중인 상황이므로 고전 컴퓨터와 연동을 해서 사용하는 것이 일반적이다.
이러한 프로세스는 데이터를 양자의 형태로 둘지 혹은 고전의 형태로 둘지와 데이터를 양자 알고리즘으로 처리할지, 고전 알고리즘으로 처리할지에 따라서 다음과 같이 나눌 수 있다.
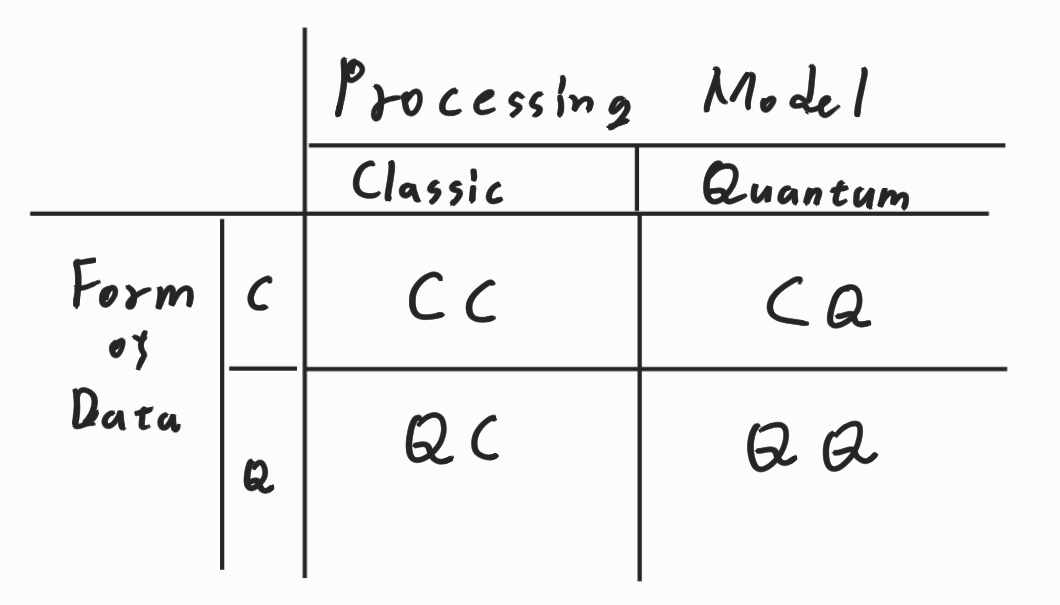
궁극적으로는 QQ가 목표겠지만 현재로써는 CQ Process나 QC Process를 이용함으로써 실용적이고 직관적인 결과를 얻어 낼 수 있다.
특히 CQ 프로세스는 머신러닝 지식이 있다면 쉽게 이해할 수 있다.
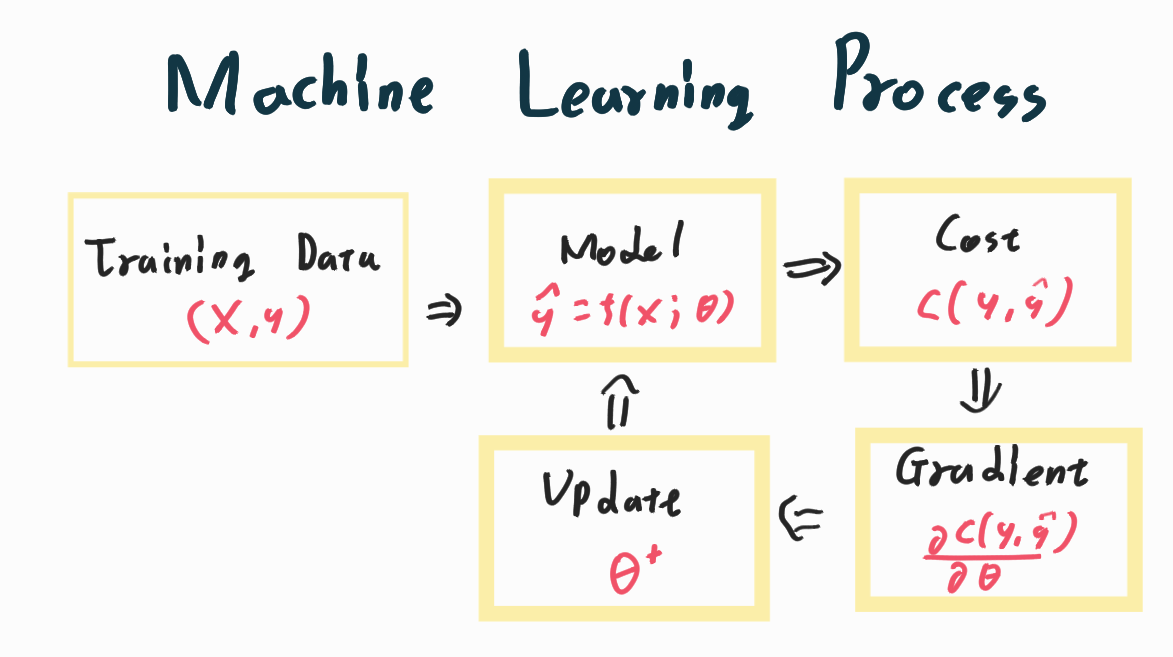
대다수의 머신러닝은 1.훈련용 데이터를 준비하고 이를 2. 모형에 넣어서 3. 비용을 계산한 뒤 4. Gradient를 이용하여 5.더 나은 모형의 모수를 찾아내는 방식으로 이뤄진다.
양자컴퓨터는 여기서 2번의 모형 스텝과 4번의 Gradient 스텝의 역할을 할 수 있다. 물론 모수는 이러한 Iteration방식이 아닌 다른 방식으로도 찾을 수 있으며 이 또한 양자컴퓨터를 이용해서 계산 가능하다.
이러한 f(x)를 양자컴퓨터에 녹여내는 것은 이론적으로는 용이하게 가능하다. 그러나 현재의 양자컴퓨터는 그 큐빗의 개수가 작을 뿐더러 무시할 수 없는 오류를 내포하고 있기 때문에, 특별한 방식의 구현이 필요하다. 이를 Variational Model이라고 말한다.
예컨데 데이터 벡터 X에 적용하면 최적의 모수 $\theta$를 뽑아주는 양자 회로를 생각해보자.
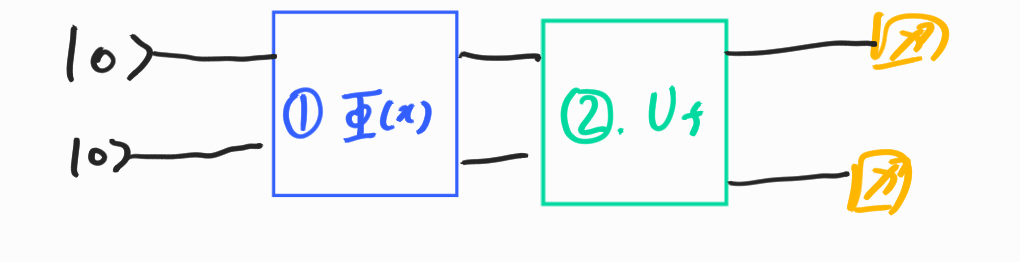
이 $\Phi(x)$ 부분은 데이터를 인코딩 시키는 부분이다. 큐빗 $\ket{0}$는 $\Phi(x)$를 통과함으로써 데이터 벡터 $\ket{x}$가 되고 이 $\ket{x}$는 \(U_f\)를 통과함으로써 어떻게든 마법적으로 $\theta$를 도출 시킨다. 모델에 따라서 이러한 회로를 가지는 행렬 \(U_f,\Phi(x)\)를 찾아내는 것이 전체적인 연구의 프레임이라고 말할 수 있다.
그러나 위와 같은 행렬들을 찾아낸다고 해서 현존하는 양자컴퓨터는 이론을 완벽하게 들어맞지 않는다. 현재의 양자컴퓨터는 오류가 크기 때문이다. 따라서 위의 행렬에 추가적인 모수 $\gamma$를 이용하여 오류를 극복하는 회로를 Variational Circuit(=parameterized circuit = ansatz)이라고 말한다.
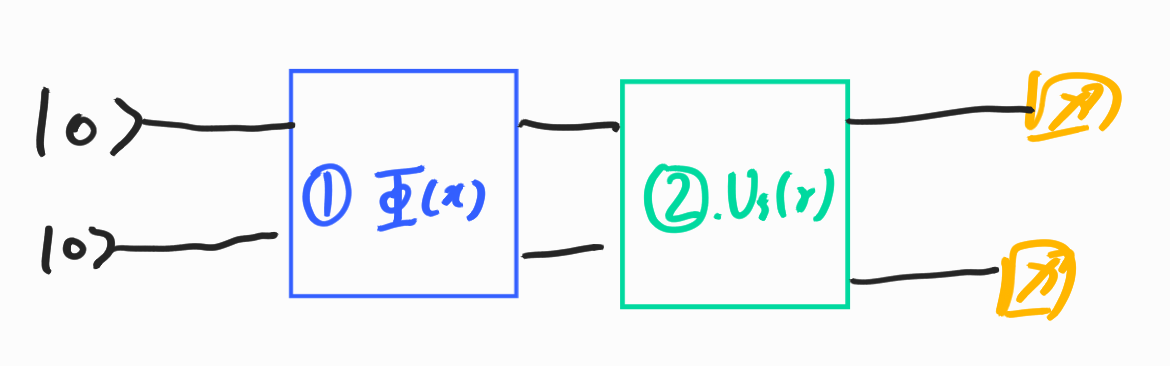
이러한 종류의 회로가 구체적으로 어떻게 오류를 극복하는 지에 대해서는 차후에 살펴보자.
양자 머신러닝은 계속 연구 중인 영역이기에 위와 같은 프레임워크를 따르지 않는 모형도 많다. 그러나 Variational Circuit에 한해서는 모형의 이해를 다음과 같이 하면 되겠다.
- 데이터가 인코딩 되는 행렬 $\Phi(x)$ 이해하기
- 인코딩 된 데이터가 처리되는 프로세스 $U_f$ 이해하기
- 프로세스를 Variational Circuit으로 바꾸는 과정 \(U_f(\gamma)\) 이해하기
이러한 프로세스를 익히는 데 가장 적절한 예시는 QAOA(;Quantum Approximated Optimization Algorithm)이다. 이를 이해해보자.
Quantum Approximated Optimization Algorithm
QAOA는 QUBO를 푸는 문제이다. 그러니 QUBO가 뭔지 부터 알아보자.
QUBO (Quadratic Unconstrained Binary Optimization)
QUBO는 말 그대로 제약이 걸리지 않은 이항 최적화 문제이다. 가장 일반적인 형태는 다음과 같다.
\[\max_{x} \sum \sum q_{ij} x_i x_j\]where \(x= (x_1,x_2,...x_n), x_i \in \{0,1\}\) and \(q_{ij} \in \mathbb{R}\)
즉, x는 0 혹은 1을 값으로 가지는 벡터이고 이들과 가중치인 \(q_{ij}\)를 계산한 값을 최대화 혹은 최소화 시키는 문제이다. 이는 일종의 Combinatorial Optimization Problem이며 대표적인 NP-Hard 문제이다.
이 문제가 적용되는 대표적인 예시로 Graph Theory의 Max-cut 문제를 들 수 있다. 예컨데 다음과 같은 그래프를 생각해보자.
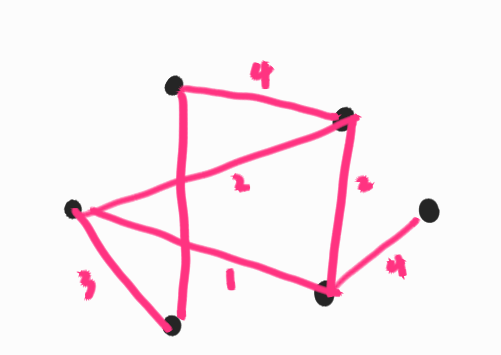
6개의 검은 점들을 두가지로 분류를 하고자 하는데 노드들이 연결된 선과 그에 할당된 수치를 기준으로 하여 이 수치가 높은 선들을 기준으로 연결시키고자 한다.
해당 문제에서 수치를 Similarity(유사도)로 해석한다면, 즉 수치가 높을 수록 점들이 가깝다고 해석한 후에 QUBO Maximization 문제를 푼다면 유사도가 높은 그룹끼리 묶어 낼 수 있다. 이는 일종의 클러스터링을 한것이라고 생각 할 수 있다. 이를 Max cut이라고 말한다.
이는 고전적으로는 모든 경우의 수를 고려해야하며 전형적인 NP-Hard 문제이다. 조금 더 응용하면 회귀분석의 변수선택 문제로도 확장할 수 있을 것 같다.
이 문제의 비용함수는 Quadratic Problem이다. 좀 더 일반화 해서 다음문제를 생각해보자.
\[C(x) = \sum_i \sum_j q_{ij }x_i x_j+\sum_i c_i x_i\]이 비용이 가장 큰 X 조합을 찾는것이 목적이 될 것 이다.
이를 구해주는 양자알고리즘을 구하는 것이 결국 최종 목표가 될것 인데, 이는 생각보다 훨씬 아름답게 구해질 수 있다. 다음을 만족하는 \(H_c\)를 구해보자.
\(H_c \ket{x} = C(x) \ket{x}\) (여기서 x는 임의의 Computational Basis e.g. \(\ket{010110}\)이다. )
우선 다음과 같은 방정식을 확인하자.
\[Z_i \ket{x} = (-1)^{x_i} \ket{x} = (1-2x_i)\ket{x}\] \[\Rightarrow \frac{(I-Z_i)}{2} \ket{x} = x_i \ket{x}\]이를 \(C(x)\)에 대입하면 다음을 얻어낼 수 있다.
\[C(x) = \sum_i \sum_j q_{ij} \frac{(I-Z_i)}{2} \frac{(I-Z_j)}{2} + \sum_i c_i \frac{(I-Z_i)}{2}\] \(= \frac{1}{4}\sum_i \sum_j q_{ij} Z_iZ_j -\frac{1}{2} \sum_i (c_i+\sum_{j} q_{ij})Z_i +\frac{1}{4}(\sum_i (\sum_j q_{ij}+2c_i)I\)
\(=: H_c\)
따라서 위와 같이 상수함수 \(C(x)\)를 Operator \(H_c\)로 변환할 수 있다.
이를 완전중첩상태 \(\ket{\psi} = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{N} \ket{x}\)에 적용시키면 다음과 같다.
\[H_c \ket{\psi} = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{N} H_c\ket{x}= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{N} C(x)\ket{x}\]앞의 상수는 공통으로 적용되므로 제외한다고 하면 즉 상태에 따라서 일종의 C(x)를 밀도로 가지는 확률밀도 함수를 얻어낼 수 있다. 따라서 알고리즘의 shot을 8000번 정도 돌리면 이 결과 값들은 확률 분포를 형성하게 된다.
위의 결과를 정리하면 다음과 같다.
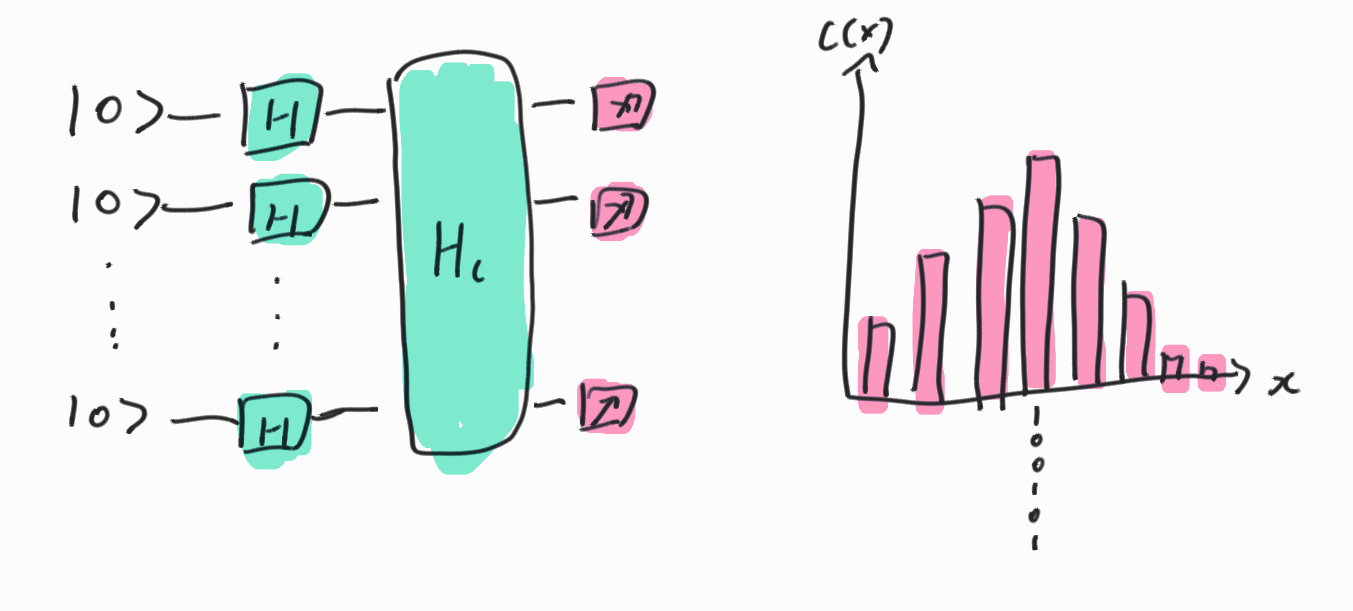
즉 이 또한 양자 중첩을 이용해서 경우의 수를 한꺼번에 계산해낸 것이다.
그러나 위의 이론과는 다르게 QUBO는 양자컴퓨터에서 안정적으로 계산되지 않는다. 이는 \(H_c\) 행렬 자체가 복잡한 꼴이기 때문에 오류가 발생하기 쉬운 것이 원인이라고 할 수 있다.
이를 훨씬 더 안정적으로 풀어 낼 수 있는 알고리즘이 QAOA 알고리즘이다.
QAOA(Quantum Approximated Optimization Algorithm)
QAOA는 다음과 같은 회로를 가진다.

여기서 \(U_c(\gamma_i) = e^{-i\gamma_i H_c}, U_M(\beta_i) = e^{-i\beta_i H_M}\) 이다. \(H_c\)는 위에서 정의한 그대로 이고 \(H_M = X^{n}\)이다.
일반적인 회로와 Variational Algorithm이 다른 점은 \(H_c\) 하나만 적용을 하는 것에서 약간 변형시킨 p개의 레이어로 늘린 점이다.
여기서 \(e^{-i \gamma H_C}\)는 지수 위에 행렬이 올라가 있는데 이는 다음과 같이 해석할 수 있다.
\[e^X = \sum \frac{1}{k!} X^k\]이 수식을 이용하면 파울리 오퍼레이터 (X,Y,Z)는 다음과 같이 해석할 수 있다.
\[e^{-i \theta X} = R_{X}(2 \theta) ,e^{-i \theta Y} = R_{Y}(2 \theta),e^{-i \theta Z} = R_{Z}(2 \theta)\]이를 해석하면 \(\theta \in (0,\pi)\)에 대해서 \(\theta = 0\)일시 움직이지 않고 \(\theta = \pi\)일시 X,Y,Z를 그대로 반환한다. 즉 \(\theta\)가 커질수록 $I$에서 \(X,Y,Z\) 방향으로 비율적으로 이동하는 것이다.
추가적으로 모든 Unitary Gate는 파울리 게이트의 선형조합으로 이루어 진다. 즉 $U = c_0 I+ c_1 X + c_2 Y + c_3 Z$이다.
따라서 $e^{-i\theta U} = e^{-i\theta c_0 I}e^{-i\theta c_1 X}e^{-i\theta c_2 Y}e^{-i\theta c_3 Z} = R_x(2c_1 \theta )R_y(2 c_2 \theta )R_z(2 c_3 \theta )$이다.
이를 해석하면 U가 원래 회전시키는 방향을 \((\theta/\pi)\) 비율만큼 줄여서 회전시키는 것이다.
정리하면 \(U_c(\gamma_i)\)는 \(H_c\)를 \(\gamma_i\)만큼 비율을 줄여 약하게 적용시킨다는 의미이다.
일반적으로 \(\gamma_i\) 는 0에서 부터 점점 상승시키는 형식으로 디자인한다. \(H_c\)가 너무 복잡한 형태였다는 것을 상기한다면 해당 알고리즘을 \(H_c\)를 비율적으로 약한 형태에서 점점 복잡한 형태로 올라가면서 원래 얻고자 했던 \(H_c\)를 통과시킨 결과를 완전하게 얻어내는 알고리즘이 되는 것이다.
\(H_M\)을 적용시키는 것은 이러한 알고리즘을 돌리기 위해서 필요한 부분이며 에너지를 반전시켜 탐색을 좀 더 잘할 수 있도록 돕는다.
이러한 방식은 오류에 대해서 비교적 강건하다. 이를 유도하는 것에 있어서는 슈뢰딩거의 방정식이나 Adiabatic Theorem을 알아야 하지만 생략하고 아래의 그림을 통해서 대략적인 감을 잡아보자.
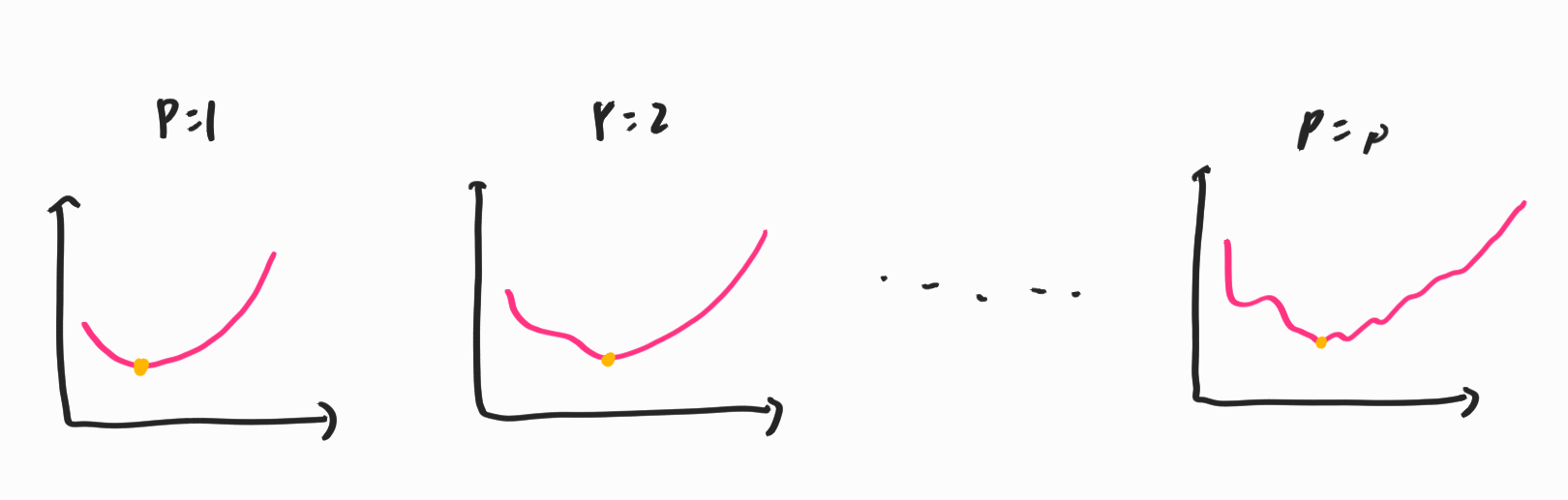
너무 복잡한 형태를 바로 적합시키는 것은 힘들기에 약한 것 부터 순차적으로 적합시키는 것으로 해석할 수 있다. 이러한 방식의 적합을 정확하게 Adiabatic Quantum Computing이라고 한다.
이 알고리즘에 추가해서 이항 X를 연속으로 확장시키거나 시작값을 좀 더 그럴싸하게 만든다던가 하는 여러가지 응용법들이 있다. 우선은 구체적인 것은 생략하고 여기까지 이해하도록 하자.