from IPython.core.display import display,HTML
display(HTML('<style>.prompt{width: 0px; min-width: 0px; visibility: collapse}</style>'))
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
실습1. Basic Gradient Descent
아래의 문제들을 Gradient Descent 방식으로 풀어보자
문제 0. 𝑓(𝑥)=𝑥2−2𝑥+1 의 최솟값을 구해보자.
선형회귀모델 $y= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon$을 가정하여 데이터 “practice_1.csv”에 대해 회귀분석을 시행하라
문제 1. 제약이 없는 LSE를 Gradient Descent 방법으로 풀어보자.
문제 2. 문제 1의 Step Size를 Backtracking Line Search를 통해서 풀어보자.
문제 3. 문제 1의 Step Size를 Exact Line Search를 통해서 풀어보자.
문제 4. 주어진 데이터의 절편은 3일때 최적값이다. 문제 1,2,3이 절편을 잘 추정했는지 확인하고 오류가 났다면 어째서 인지, 어떻게 해결할 수 있을지에 대해서 생각해보자.
문제 5. 위의 각 결과물의 이터레이션에 따른 오차를 비교해주는 그림을 그려보자.
Gradient Descent Method는 다음과 같다.
Gradient Descent
For unconstrained optimization problem whose objective function $f(x)$ is smooth convex function, sequence ${x_{k}}$ that has folloing iteration form converges to problem’s solution $x^*$ such that $x^* = \underset{x}{argmin} f(x)$ under appropriate step size $t_k$ $ x^{(k+1)} = x^{(k)} - t_k \nabla f(x^{(k)})$
문제 0. 몸풀기 $f(x) = x^2-2x+1$의 최솟값을 구해보자.
주어진 문제는 다음과 같은 mathematical optimization 문제라고 볼 수 있다.
$\underset{x}{min} \ x^2 -2x +1$
이는 unconstrained convex optimization 문제이므로 기본적인 Gradient Descent를 이용해서 풀 수 있다.
Iteration Form을 유도해내면 다음과 같다.
$x^{(k+1)} = x^{(k)} - t_k \nabla f(x^{(k)}) \\ \quad =x^{(k)}- t_k (2x^{(k)}-2)$
이 식을 이용해서 Gradient Descent를 설계해보자.
우선 초기값 $x_0$ 및 현재값 $x_k$ 가 들어갈 인스턴스와 결과물을 저장해줄 공간을 정의해주자.
## 초기값 설정 (x-initial value)
x_init = np.array([100])
## 현재값 설정 (x-temporary value)
x_temp = x_init
## 결과물 공간 (x-result)
x_result = pd.DataFrame(x_init,columns=["x"])
다음으로 스텝사이즈(learning-rate)와 이터레이션 횟수를 지정해주자. 스텝사이즈를 지정해주는 것은 또다른 추론들이 필요하지만 간단하게 고정된 스텝사이즈를 사용하자. 이터레이션 횟수 또한 100으로 적게 정해주자.
## 스텝사이즈 t 설정
t=0.1
## 이터레이션 횟수 설정
iter = 100
마지막으로 이터레이션 폼을 구현하자.
for i in range(iter):
# 이터레이션 공식
x_temp = x_temp - 2*t*(2*x_temp-2)
# 결과물 저장
x_result = x_result.append(pd.DataFrame(np.array([x_temp]),columns=["x"]),ignore_index=True)
x_result
| x | |
|---|---|
| 0 | 100.0000 |
| 1 | 60.4000 |
| 2 | 36.6400 |
| 3 | 22.3840 |
| 4 | 13.8304 |
| ... | ... |
| 96 | 1.0000 |
| 97 | 1.0000 |
| 98 | 1.0000 |
| 99 | 1.0000 |
| 100 | 1.0000 |
101 rows × 1 columns
주어진 문제를 최소화 시키는 closed form solution은 1이므로 이터레이션 폼이 정답을 잘 찾아냈다고 말 할 수 있다.
문제 1. 제약이 없는 LSE를 Gradient Descent 방법으로 풀어보자.
LSE는 오차의 제곱합(SSE;Sum of Squared Error)를 최소화 시켜주는 추정량을 찾음으로써 모수를 추정하는 방법이다.
선형 회귀모델 $y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \epsilon_i$ or $y= X\beta+\epsilon$의 SSE는 다음과 같다.
$f(\beta) = \sum_i^n \epsilon_i^2 = \epsilon^t\epsilon \\ \quad= (y-X\beta)^t(y-X\beta) \\ \quad = y^ty-2\beta^tX^ty + \beta^tX^tX\beta$
이때 목적함수 $f(\beta)$는 L2-Norm의 Affine Transformation 꼴이므로 Convex Function이다.
따라서 이에 대한 Convex Optimization Problem을 다음과 같이 설계 할 수 있다.
$\underset{\beta}{min} {y^ty-2\beta^tX^ty+\beta^tX^tX\beta}$
이에 대한 Gradient를 구하면 다음과 같다.
$\frac{\delta}{\delta \beta}{y^ty-2\beta^tX^ty+\beta^tX^tX\beta} \\ \quad = {-2y^tX+2X^tX\beta}$
따라서 이터레이션 폼은 다음과 같은 형태를 띈다.
$x^+ = x - t \nabla f(x) \\ \quad = x - 2t(X^tX\beta-y^tX)$
우선 위에서 구한 공식을 이용해 현재의 $\beta$값을 넣으면 현재의 Gradient를 계산해주는 함수를 짜자.
def gradient(beta) :
return((x_mat.transpose()@x_mat@beta-x_mat.transpose()@y_mat))
데이터를 불러온 다음 X와 Y를 나눠서 행렬에 저장해주자
df = pd.read_csv("practice.csv")
df.head()
| y | x0 | x1 | x2 | |
|---|---|---|---|---|
| 0 | 463.029335 | 1.0 | 93.125595 | 45.841138 |
| 1 | 171.681165 | 1.0 | 71.924815 | 4.365620 |
| 2 | 402.521038 | 1.0 | 60.908435 | 46.282571 |
| 3 | 293.383192 | 1.0 | 60.735983 | 28.166286 |
| 4 | 554.876057 | 1.0 | 26.853625 | 82.930904 |
x_mat = df.iloc[:,1:4]
y_mat = df.iloc[:,0]
Gradient Descent의 경우 $ \parallel \nabla f(x) \parallel_2$가 충분히 작아질 때, Ealry Stopping을 해준다. 이를 구현해주는 코드도 짜보자.
나머지는 0번 문제에서 했던 것과 똑같은 절차를 취해주면 된다.
우선 Initial Point 및 Place Holder 만들어주자
## 기본값 설정 (beta-temporary value)
beta_init = [1,1,1]
## 현재값 설정 (beta-temporary value)
beta_temp = beta_init
## 결과물 공간 (Gradient Descent Result A)
GD_result_A = pd.DataFrame([beta_init],columns=["beta0","beta1","beta2"])
다음으로 Step Size를 지정해주자. 0.01 정도면 충분히 낮은 수치라고 말할 수 있다.
t_fixed= 0.01
위에서 정의해준 Gradient를 이용해서 이터레이션 폼을 짜주자.
for i in range(1000) :
beta_temp = beta_temp - 2*t_fixed*(gradient(beta_temp))
GD_result_A = GD_result_A.append(pd.DataFrame(np.array([beta_temp]),columns=["beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.0001 : break
GD_result_A
| beta0 | beta1 | beta2 | |
|---|---|---|---|
| 0 | 1.000000e+00 | 1.000000e+00 | 1.000000e+00 |
| 1 | 6.222271e+03 | 3.348455e+05 | 4.006690e+05 |
| 2 | -7.547918e+08 | -4.401388e+10 | -4.542721e+10 |
| 3 | 9.174036e+13 | 5.402243e+15 | 5.470796e+15 |
| 4 | -1.115184e+19 | -6.575143e+20 | -6.642294e+20 |
| ... | ... | ... | ... |
| 996 | NaN | NaN | NaN |
| 997 | NaN | NaN | NaN |
| 998 | NaN | NaN | NaN |
| 999 | NaN | NaN | NaN |
| 1000 | NaN | NaN | NaN |
1001 rows × 3 columns
Step Size 설정이 잘 되지 못해서 값이 발산해버렸다. 0.01이면 충분히 낮은 수치라고 볼 수 있지만 SSE 함수에 포함된 데이터들이 필요로 하는 스텝사이즈는 그보다 훨신 낮은 수치이기 때문이다. 따라서 Step Size를 극단적으로 낮춰준 후 다시 돌려주자.
t_fixed = 0.00000001
## 초기값
beta_init = [1,1,1]
## 현재값
beta_temp = beta_init
## 전체 결과물 저장소
GD_result_A = pd.DataFrame([beta_init],columns=["beta0","beta1","beta2"])
for i in range(1000) :
beta_temp = beta_temp - 2*t_fixed*(gradient(beta_temp))
GD_result_A = GD_result_A.append(pd.DataFrame(np.array([beta_temp]),columns=["beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.01 : break
GD_result_A
| beta0 | beta1 | beta2 | |
|---|---|---|---|
| 0 | 1.000000 | 1.000000 | 1.000000 |
| 1 | 1.006221 | 1.334844 | 1.400668 |
| 2 | 1.011688 | 1.625674 | 1.755908 |
| 3 | 1.016491 | 1.877892 | 2.071191 |
| 4 | 1.020712 | 2.096243 | 2.351323 |
| ... | ... | ... | ... |
| 996 | 1.056884 | 2.017191 | 6.016294 |
| 997 | 1.056889 | 2.017191 | 6.016294 |
| 998 | 1.056895 | 2.017191 | 6.016294 |
| 999 | 1.056900 | 2.017191 | 6.016294 |
| 1000 | 1.056905 | 2.017191 | 6.016294 |
1001 rows × 3 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_A)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_A,s=200,marker="o")
plt.show()
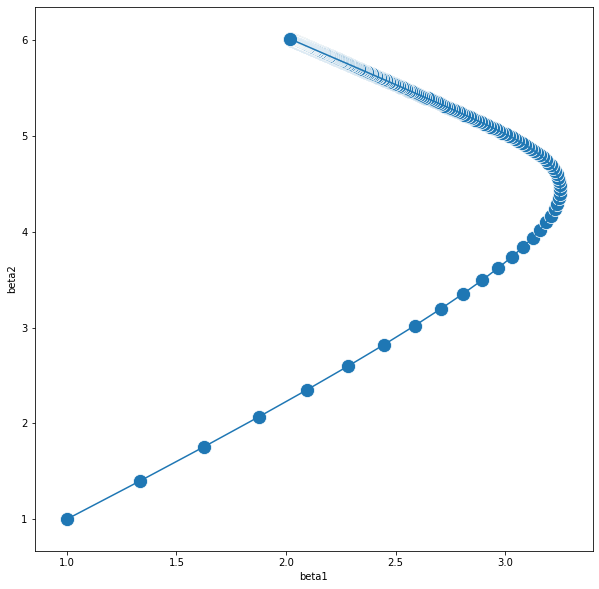
이렇게 나온 결과물을 보면 계수들은 그럭저럭 잘 추정을 해냈지만 절편값은 추정을 잘 해주지 못했다. 정확하게는 계수는 빠르게 수렴한 반면 절편은 수렴이 비교적 매우 늦기 때문에 일어난 상황이다. 이는 Gradient Descent의 근본적인 단점이라고 볼 수 있는 데 이에 대해서는 다른 문제들을 본 후 다시 살펴보자.
문제 2. 문제 1의 Step Size를 Backtracking Line Search를 통해서 풀어보자.
문제 1번에서는 두 가지 문제가 발생했다고 볼 수 있다. 하나는 스텝 사이즈를 자의적으로 정해주는 것이 어렵다는 점이고, 또 하나는 절편을 잘 추정해주지 못했다는 점이다. 우선 전자의 문제를 해결해주기 위해 Backtracking Line Search를 사용해주자.
Backtracking Line Search는 다음과 같은 알고리즘이다.
- 우선 initial step size $t_0$를 임의로 정해준다.
- 알고리즘의 하이퍼 파라미터인 $\alpha \in (0,0.5] , \beta \in (0,1)$를 임의로 정해주자.
- 다음의 조건을 체크하고 조건이 성립하지 않을 때 까지 $t = \beta t$를 넣어주며 t를 축소해주자.
$ f(x^+) > f(x) - \alpha t \parallel \nabla f(x) \parallel_2^2$ - 조건이 성립하지 않는다면 구해진 t값을 이용해서 Gradient Descent Step을 1회 진행하자.
따라서 이 조건을 구현해 주기 위해서 현재의 t값을 넣었을 때 조건문을 체크해주는 함수를 짜보자.
def backtracking(alpha,t) :
beta_plus = beta_temp - 2*t_temp*(x_mat.transpose()@x_mat@beta_temp-x_mat.transpose()@y_mat)
res_plus = sum((y_mat-x_mat@beta_plus)**2)
res = x_mat.transpose()@x_mat@beta_temp-x_mat.transpose()@y_mat
res_temp = sum((y_mat-x_mat@beta_temp)**2)-alpha*t_temp*sum(res**2)
return(res_plus>res_temp)
나머지는 마찬가지로 초기값 및 하이퍼파라미터를 설정해주자
## 모수 초기값
beta_init = np.array([1,1,1])
## 모수 현재값
beta_temp = beta_init
## 스텝 초기값
t_init = np.array([0.5])
## 스텝 현재값
t_temp = t_init
## 전체 결과물 저장소
GD_result_B = pd.DataFrame([[*t_init,*beta_init]],columns=["Step","beta0","beta1","beta2"])
## 하이퍼 파라미터
alpha = 0.5
beta = 0.7
backtracking line search는 while 문을 이용하여 구현을 해주면 된다.
for i in range(1000) :
while (backtracking(alpha,t_temp)):
t_temp = t_temp * beta
beta_temp = beta_temp - 2*t_temp*gradient(beta_temp)
GD_result_B = GD_result_B.append(pd.DataFrame([[*t_temp,*beta_temp]],columns=["Step","beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.01 : break
GD_result_B
| Step | beta0 | beta1 | beta2 | |
|---|---|---|---|---|
| 0 | 5.000000e-01 | 1.000000 | 1.000000 | 1.000000 |
| 1 | 1.091907e-07 | 1.067931 | 4.656191 | 5.374923 |
| 2 | 1.091907e-07 | 1.045869 | 3.064698 | 4.333640 |
| 3 | 1.091907e-07 | 1.053248 | 3.258541 | 4.998424 |
| 4 | 1.091907e-07 | 1.050977 | 2.923954 | 5.049299 |
| ... | ... | ... | ... | ... |
| 996 | 1.091907e-07 | 1.108915 | 2.016760 | 6.015847 |
| 997 | 1.091907e-07 | 1.108972 | 2.016760 | 6.015846 |
| 998 | 1.091907e-07 | 1.109028 | 2.016759 | 6.015846 |
| 999 | 1.091907e-07 | 1.109085 | 2.016759 | 6.015845 |
| 1000 | 1.091907e-07 | 1.109142 | 2.016758 | 6.015845 |
1001 rows × 4 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_B)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_B,s=200,marker="o")
plt.show()
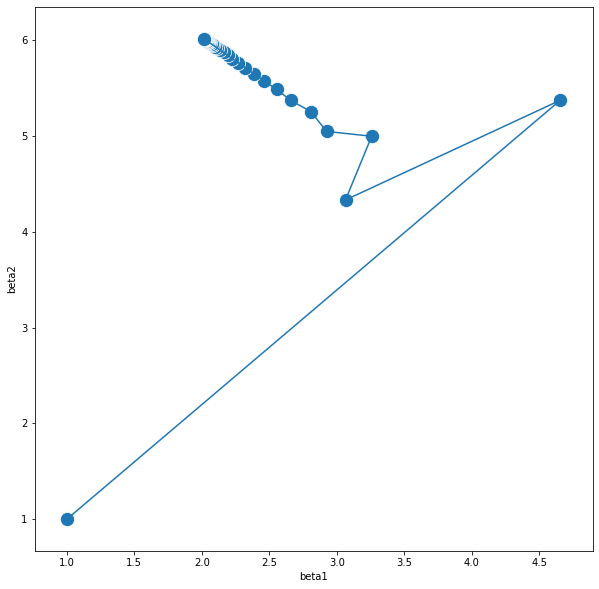
결과물은 마찬가지로 계수는 잘 찾아줬고 절편은 잘 찾아주지 못했다.
문제 C. A의 Step Size를 Exact Line Search를 통해서 풀어보자.
Gradient Descent에서 Convergence Analysis를 해보면 Strong Convexity Constant $\mu$와 Lipschitz Constant L을 찾아서 평균의 역수를 사용함으로써 최적의 Exact Step Size를 찾을 수 있다. 많은 방식이 있지만 이 문제에 대해서는 아래를 만족하는 Constant를 찾아서 구해줄 수 있다.
$ LI \prec \nabla^2 f(x) \prec mI$
$\nabla^2 f(x) = \nabla { \nabla f(x)} \\ \qquad \quad = \nabla {-2y^tX+2X^tX\beta } \\ \qquad \quad = 2X^tX$
Quadratic Form Theorem을 쓰면 아래와 같은 관계식을 얻을 수 있다.
$\lambda_p \leq \frac{x^t A x}{x^t x} \leq \lambda_1$
$\lambda_p x^t x \leq x^t A x \leq \lambda_1 x^t x$
$ \lambda_p I \leq A \leq \lambda_1 I$
따라서 Hessian Matrix의 아이젠 밸류의 최대값과 최소값이 Lipschit Constant L과 Strong Convexity Constant $\mu$가 된다.
따라서 아래와 같이 분해를 해준 뒤 이론상의 정확한 step size를 찾아주자
eigen = np.linalg.svd(2*x_mat.transpose()@x_mat)[1]
t_fixed = 2/(np.min(eigen)+np.max(eigen))
t_fixed
1.6452166570173455e-07
이제 앞에서 진행한 것과 똑같이 코딩을 해주자
## 초기값
beta_init = [1,1,1]
## 현재값
beta_temp = beta_init
## 전체 결과물 저장소
GD_result_C = pd.DataFrame([beta_init],columns=["beta0","beta1","beta2"])
for i in range(1000) :
beta_temp = beta_temp - 2*t_fixed*((x_mat.transpose()@x_mat@beta_temp-x_mat.transpose()@y_mat))
GD_result_C = GD_result_C.append(pd.DataFrame(np.array([beta_temp]),columns=["beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.01 : break
GD_result_C
| beta0 | beta1 | beta2 | |
|---|---|---|---|
| 0 | 1.000000 | 1.000000 | 1.000000 |
| 1 | 1.102353 | 6.508917 | 7.591857 |
| 2 | 1.000401 | 0.104250 | 1.887543 |
| 3 | 1.102689 | 5.843695 | 8.250053 |
| 4 | 1.000703 | -0.388961 | 2.376475 |
| ... | ... | ... | ... |
| 996 | 1.088479 | -0.865018 | 3.105686 |
| 997 | 1.186289 | 4.897940 | 8.925389 |
| 998 | 1.088652 | -0.864764 | 3.105942 |
| 999 | 1.186453 | 4.897683 | 8.925130 |
| 1000 | 1.088825 | -0.864509 | 3.106199 |
1001 rows × 3 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_C)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_C,s=200,marker="o")
plt.show()

이론 상의 정확한 stepsize를 구해줬음에도 수렴을 제대로 해주지 못했다. 스텝을 약간만 줄인 뒤 다시 한번 더 확인해보자.
## 초기값
beta_init = [1,1,1]
## 현재값
beta_temp = beta_init
## 전체 결과물 저장소
GD_result_C = pd.DataFrame([beta_init],columns=["beta0","beta1","beta2"])
eigen = 2*np.linalg.svd(x_mat.transpose()@x_mat)[1]
t_fixed = 1.9/(np.min(eigen)+np.max(eigen))
for i in range(1000) :
beta_temp = beta_temp - 2*t_fixed*((x_mat.transpose()@x_mat@beta_temp-x_mat.transpose()@y_mat))
GD_result_C = GD_result_C.append(pd.DataFrame(np.array([beta_temp]),columns=["beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.01 : break
GD_result_C
| beta0 | beta1 | beta2 | |
|---|---|---|---|
| 0 | 1.000000 | 1.000000 | 1.000000 |
| 1 | 1.097236 | 6.233471 | 7.262264 |
| 2 | 1.010086 | 0.714933 | 2.427234 |
| 3 | 1.088826 | 5.070852 | 7.383132 |
| 4 | 1.018235 | 0.689745 | 3.379496 |
| ... | ... | ... | ... |
| 996 | 1.133143 | 2.016560 | 6.015638 |
| 997 | 1.133223 | 2.016559 | 6.015638 |
| 998 | 1.133304 | 2.016559 | 6.015637 |
| 999 | 1.133384 | 2.016558 | 6.015636 |
| 1000 | 1.133464 | 2.016557 | 6.015636 |
1001 rows × 3 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_C)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_C,s=200,marker="o")
plt.show()
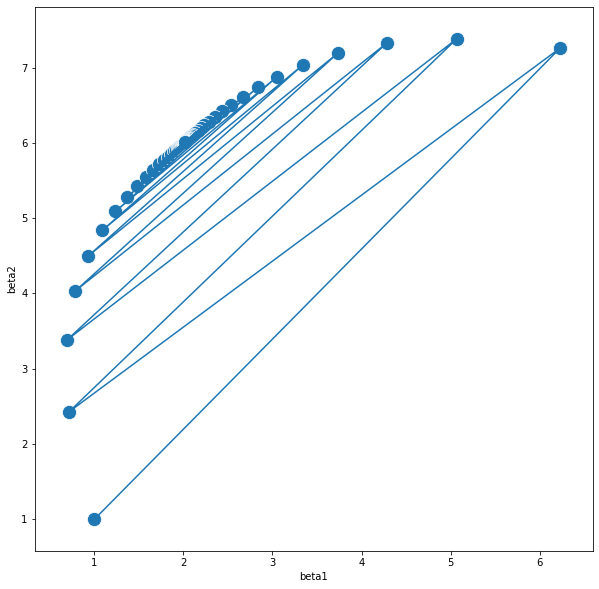
이제는 제대로 수렴이 되었다. 따라서 알 수 있는 점은 이론상의 스텝사이즈가 수렴의 분기점이 될수 있다는 점이다.
이제 두번째 문제점이었던 절편의 수렴 문제에 대해서 해결해보자.
이론상의 exact한 t step은 선형모델에서는 Design Matrix의 내적 형태의 아이젠 밸류에 의존한다.
이 아이젠 밸류는 Design Matrix의 공분산과 연결되어 있다. 그렇다면 생각해 볼 수 있는 것은 선형모델의 LSE에서의 Gradient Descent는 데이터의 분산에 크게 영향을 받는다 라고 말 할 수 있다. 디자인 매트릭스에서 서로 꼬이기 마련이지만, 절편에 해당하는 데이터는 모두 1로, 분산이 0 인 반면 나머지 데이터들의 분산은 800가량을 차지한다. 이 불균형이 계수와 절편의 수렴 불균형에 영향을 미치는 것으로 보인다. 따라서 스케일링을 통해서 수정을 해줄 수 있겠다.
np.cov(x_mat.T)
array([[ 0. , 0. , 0. ],
[ 0. , 812.12127197, 17.96454473],
[ 0. , 17.96454473, 792.58225054]])
스케일링 후 A,B,C를 다시 풀어보자.
스케일링 기법은 편의상 사이킷런의 StandardScaler를 사용해 주었다.
from sklearn import preprocessing
x_scaled = preprocessing.scale(x_mat)
y_scaled = preprocessing.scale(y_mat)
스케일링 이후의 Gradient를 구해주는 함수도 짜주자.
def gradient_scaled(beta) :
return((x_scaled.transpose()@x_scaled@beta-x_scaled.transpose()@y_scaled))
스케일링 후 Fixed Step GD
## 초기값
beta_init = [0,1,1]
## 현재값
beta_temp = beta_init
## 전체 결과물 저장소
GD_result_AS = pd.DataFrame([beta_init],columns=["beta0","beta1","beta2"])
## step size 지정
t_fixed = 0.0001
## 이터레이션 돌리기
for i in range(1000) :
beta_temp = beta_temp - 2*t_fixed*gradient_scaled(beta_temp)
GD_result_AS = GD_result_AS.append(pd.DataFrame(np.array([beta_temp]),columns=["beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.001 : break
GD_result_AS
| beta0 | beta1 | beta2 | |
|---|---|---|---|
| 0 | 0.0 | 1.000000 | 1.000000 |
| 1 | 0.0 | 0.863278 | 0.985162 |
| 2 | 0.0 | 0.753966 | 0.973903 |
| 3 | 0.0 | 0.666567 | 0.965386 |
| 4 | 0.0 | 0.596686 | 0.958964 |
| ... | ... | ... | ... |
| 996 | 0.0 | 0.317707 | 0.941086 |
| 997 | 0.0 | 0.317707 | 0.941086 |
| 998 | 0.0 | 0.317707 | 0.941086 |
| 999 | 0.0 | 0.317707 | 0.941086 |
| 1000 | 0.0 | 0.317707 | 0.941086 |
1001 rows × 3 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_AS)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_AS,s=200,marker="o")
plt.show()
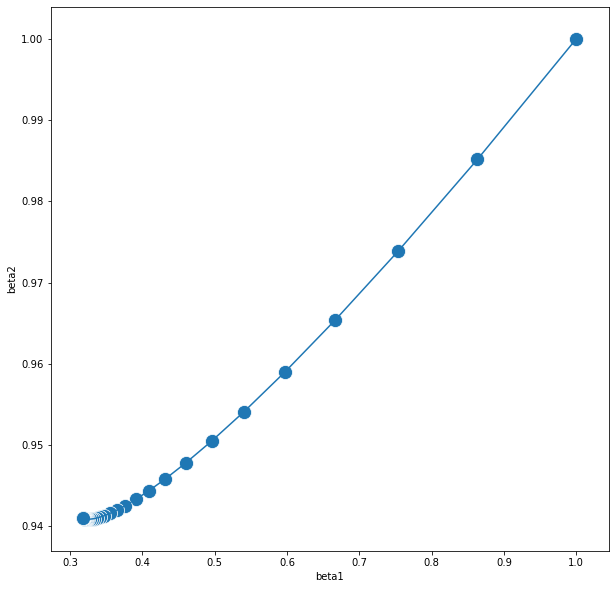
스케일링 후 BackTracking Line Search
Scaled 함수에 맞춰서 Backtracking 함수를 다시 짜주자.
def backtracking_scaled(alpha,t) :
beta_plus = beta_temp - 2*t_temp*(x_scaled.transpose()@x_scaled@beta_temp-x_scaled.transpose()@y_scaled)
res_plus = sum((y_scaled-x_scaled@beta_plus)**2)
res = x_scaled.transpose()@x_scaled@beta_temp-x_scaled.transpose()@y_scaled
res_temp = sum((y_scaled-x_scaled@beta_temp)**2)-alpha*t_temp*sum(res**2)
return(res_plus>res_temp)
## 모수 초기값
beta_init = np.array([0,1,1])
## 모수 현재값
beta_temp = beta_init
## 스텝 초기값
t_init = np.array([0.5])
## 스텝 현재값
t_temp = t_init
## 전체 결과물 저장소
GD_result_BS = pd.DataFrame([[*t_init,*beta_init]],columns=["Step","beta0","beta1","beta2"])
## 하이퍼 파라미터
alpha = 0.5
beta = 0.7
## 이터레이션 돌리기
for i in range(1000) :
while (backtracking_scaled(alpha,t_temp)):
t_temp = t_temp * beta
beta_temp = beta_temp - 2*t_temp*gradient_scaled(beta_temp)
GD_result_BS = GD_result_BS.append(pd.DataFrame([[*t_temp,*beta_temp]],columns=["Step","beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.001 : break
GD_result_BS
| Step | beta0 | beta1 | beta2 | |
|---|---|---|---|---|
| 0 | 5.000000e-01 | 0.0 | 1.000000 | 1.000000 |
| 1 | 8.142068e-04 | 0.0 | -0.113204 | 0.879186 |
| 2 | 8.142068e-04 | 0.0 | 0.590754 | 0.995698 |
| 3 | 8.142068e-04 | 0.0 | 0.144129 | 0.896812 |
| 4 | 8.142068e-04 | 0.0 | 0.428400 | 0.975238 |
| ... | ... | ... | ... | ... |
| 996 | 7.405566e-10 | 0.0 | 0.317707 | 0.941086 |
| 997 | 7.405566e-10 | 0.0 | 0.317707 | 0.941086 |
| 998 | 7.405566e-10 | 0.0 | 0.317707 | 0.941086 |
| 999 | 7.405566e-10 | 0.0 | 0.317707 | 0.941086 |
| 1000 | 7.405566e-10 | 0.0 | 0.317707 | 0.941086 |
1001 rows × 4 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_BS)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_BS,s=200,marker="o")
plt.show()
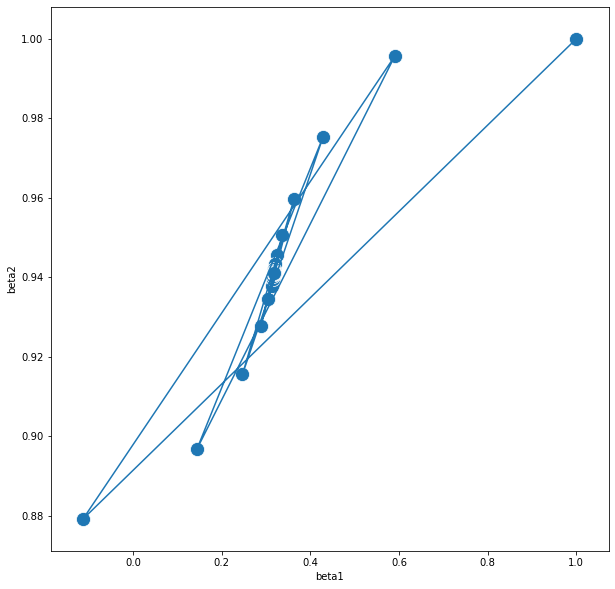
스케일링 후 Exact Line Search
위에서와 마찬가지로 Exact-Fixed Step을 계산해주자.
eigen = 2*np.linalg.svd(x_scaled.transpose()@x_scaled)[1]
t_fixed = 1.8/(np.min(eigen)+np.max(eigen))
t_fixed
0.0008802889903057032
## 초기값
beta_init = [0,1,1]
## 현재값
beta_temp = beta_init
## 전체 결과물 저장소
GD_result_CS = pd.DataFrame([beta_init],columns=["beta0","beta1","beta2"])
## 이터레이션 돌리기
for i in range(1000) :
beta_temp = beta_temp - 2*t_fixed*gradient_scaled(beta_temp)
GD_result_CS = GD_result_CS.append(pd.DataFrame(np.array([beta_temp]),columns=["beta0","beta1","beta2"]),ignore_index=True)
if sum(gradient(beta_temp)**2)**(1/2) < 0.001 : break
GD_result_CS
| beta0 | beta1 | beta2 | |
|---|---|---|---|
| 0 | 0.0 | 1.000000 | 1.000000 |
| 1 | 0.0 | -0.203553 | 0.869381 |
| 2 | 0.0 | 0.716992 | 1.016173 |
| 3 | 0.0 | 0.011059 | 0.868236 |
| 4 | 0.0 | 0.553808 | 1.008583 |
| ... | ... | ... | ... |
| 996 | 0.0 | 0.317707 | 0.941086 |
| 997 | 0.0 | 0.317707 | 0.941086 |
| 998 | 0.0 | 0.317707 | 0.941086 |
| 999 | 0.0 | 0.317707 | 0.941086 |
| 1000 | 0.0 | 0.317707 | 0.941086 |
1001 rows × 3 columns
plt.figure(figsize=(10,10))
sns.lineplot(x="beta1", y="beta2",
sort=False, data=GD_result_CS)
sns.scatterplot(x="beta1", y="beta2",data=GD_result_CS,s=200,marker="o")
plt.show()
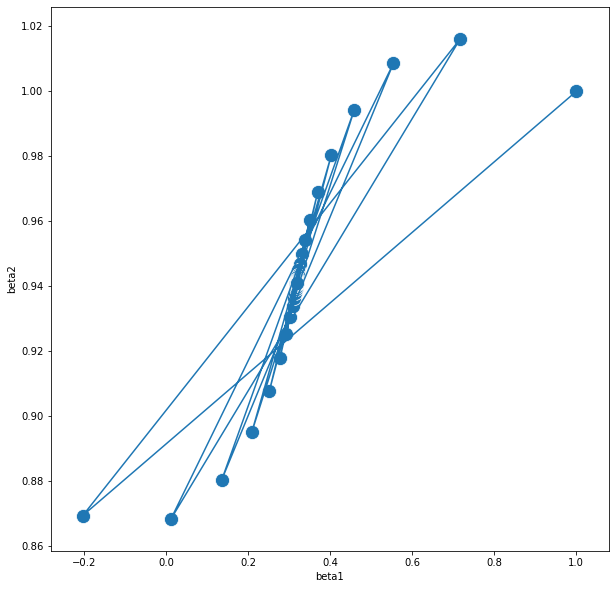
세 가지 결과물이 모두 목표로 하는 값에 잘 수렴한 것으로 보인다.
문제 D. 위의 각 결과물의 이터레이션에 따른 오차를 비교해주는 그림을 그려보자.
마지막으로 위의 세가지 결과물을 그림으로 표현해보자.
target_beta = [0,0.317707,0.941086]
GD_Total_Score = pd.concat([GD_result_AS.apply(lambda x : sum((target_beta-x)**2)/2 ,axis=1),GD_result_BS.apply(lambda x : sum((target_beta-x[1:4])**2)/2 ,axis=1),GD_result_CS.apply(lambda x : sum((target_beta-x)**2)/2 ,axis=1)],axis=1)
GD_Total_Score.columns = ["Fixed Step","BackTracking","Exact"]
plt.figure(figsize=(20,10))
sns.lineplot(data=GD_Total_Score.iloc[:20], palette="tab10", linewidth=2.5)
plt.show()
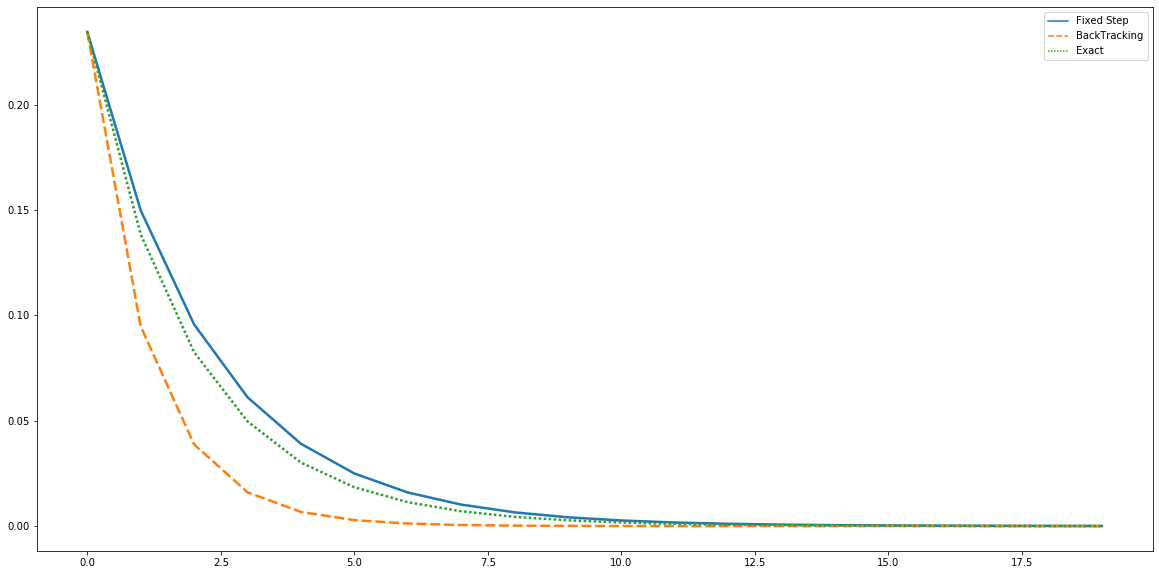
결론
- 직접 구현해본 결과 Gradient Descent를 잘 구현하기 위해서는 스케일링과 Backtraking Line Search가 필수적임을 알게 되었다.
- Exact Line Search를 위해서 Hessian Matrix를 감싸는 적절한 범위를 찾아야 하는데 이를 위해서는 Spectral Decomposition을 해줌으로써 구할 수 있다.
- Exact Line Search를 통해서 구한 Step Size는 Gradient Descent 수렴의 분기가 된다.
보완점
- Objective Function을 SSE가 아니라 MSE를 쓴다면 결국 분산의 차이에 대한 보정이 들어가서 스케일링 없이도 어느정도 가속화가 될것으로 생각된다.
- 더 많은 변수, 더 많은 데이터, 더 먼 시작점에서 어떤 식으로 변할 지에 대해서 생각해보자.
Boyd,S. & Vandenberghe, L. (2004) Convex Optimization.Cambridge, UK: Cambridge Press
Tibshirani,R. “Gradient Descent” Convex Optimization, Oct. 2019, Carnegie Mellon University, Pittsburgh
