H.G Min

H.G Min

Yonsei University,Korea Mar.14-present
- M.A. expected in applied statitstics
- B.A. in applied statistics

$\def\ket#1{\mid #1 \rangle}$

1. Linear Equation

$Ax = b$ 라는 연립 방정식은 우리가 중학교 때부터 보던 가장 대표적인 방정식이자, 무수히 많은 분야에서 필요로 하는 fundamental한 방정식이다.

물론 학부 수준의 기본적인 선형대수학에서 위의 문제의 근을 찾는것을 해왔기 때문에 위의 식을 만족하는 근 x를 찾는 것은 다음과 같이 알려져 있다.

$Ax= b$ for known $A,b$를 만족하는 근 x는 다음과 같다.

1) If $b \notin C(A) $, then There exists no x that hold Ax=b (불능)

2) If $b \in C(A)$ and A is non-singular, then $x = A^{-1}b$

3) If $b \in C(A)$ and A is singular, then $x = A^{-}b + C(A)^{\perp}$ (부정)

일반적으로는 문제에 선형방정식이 사용될때는 Ax의 결과물로서 b를 관측하고 모르는 x를 추정하기 때문에 1과 같은 사례는 잘 발생하지 않는다. 따라서 2와 3의 사례에만 집중하면 되는데, 이 경우 A의 역행렬을 안다면 위와 같은 문제가 매우 쉽게 풀림을 알 수 있다.

그러나 A의 역행렬을 구하기가 매우 어렵다는 것이 문제이다. 이 어렵다는 의미는 수학적으로 어렵다는 의미가 아니라 전산적으로 구하기가 어렵다는 것이다.

여러 프로그래밍 언어에서 inverse matrix를 구해주는 함수가 있고 이들은 시간이 오래 걸릴지 역행렬을 구해주기는 한다. 물론 SVD를 이용해서 g-inverse도 구할 수 있다.

그러나 이러한 방식은 시간이 너무 오래걸린다. 따라서 이와 같은 방식을 피해 최적화 기법을 기반으로 문제를 푸는 방법도 연구가 깊이 되고 있다. (Convex Optimization의 Linear Programming)

그러나 양자컴퓨터를 이용하면 역행렬을 곧바로 추정하는 방식으로 Linear Programming을 해결할 수 있다. 이것이 바로 HHL Algorithm이다.

2. HHL Algorithm

HHL Algorithm에 대해서

HHL Algorithm은 Harrow-Hassidim-Lloyd Algorithm의 줄임말로 2009년에 발표된 양자컴퓨터를 이용한 Linear Programming 기법이다.

기존의 고전 컴퓨터를 이용한 Linear Programming 기법의 경우 $O(Nsklog(1/\epsilon))$의 효율로 문제를 푼 반면 HHL Algorithm은 문제를 $O(\log (N)s^2k^2/\epsilon)$의 효율로 문제를 풀 수 있다. 여기서 N은 행렬 A의 Size를 의미하며, s는 A의 Sparsity, k는 제약식의 개수이다.

보다시피 행렬 사이즈 N에 대해서 지수적인 효율증가를 보이는 반면, 오차율 $\epsilon$에 대해서는 역으로 지수적인 효율 경감을 보인다. 따라서 HHL Algorithm은 대용량 데이터에 대해 특화가 되어 있지만, 나온 결과물의 근을 어디까지나 추정값으로 구해준다는 단점이 있다고 말할 수 있다.

현재까지 양자컴퓨터에서 나온 Linear Programming 기법은 HHL Algorithm을 응용한 경우가 대다수 이므로 HHL Algorithm의 한계는 양자컴퓨터의 한계와 일치한다고도 말할 수 있다.

여기까지가 HHL Algorithm에 대한 대략적인 설명이다. 이제 HHL Algorithm의 처음부터 끝까지 모두 살펴보자.

사전 셋팅

HHL Algorithm을 사용하기 위해서는 기본적인 문제의 세팅이 필요하다.

$Ax = b$

where A is $N \times N$ Hermitian Matrix, b is unit vector

  • Hermitian Matrix는 Symmetric Matrix의 복소수 확장판이다. 일반적인 Symmetric Matrix의 정의가 ${a_{ij}}={a_{ji}}$라면 Hermitian Matrix는 ${a_{ij}} = {\bar{a}_{ji}}$로 정의된다.

  • Unit Vector라고 함은 Norm이 1인 벡터를 의미한다.

  • 언뜻보기에 굉장히 강한 정의인것 처럼 보이지만 모든 선형방정식은 위와 같은 형태로 바꿀수 있다.

    • $Ax = b $ (A와 b에 조건은 없음)
      • 위의 식에 대해서 양변의 좌측에 $A^t(or A^H)$를 곱하자
    • $A^tAx=A^tb$
      • 좌변의 행렬 $A^tA$는 Symmetric Matrix의 정의에 부합한다. 이 식의 양변에 $\parallel A^tb\parallel$를 나누어 주자.
    • $\frac{1}{\parallel A^tb\parallel} A^tAx =\frac{A^tb}{\parallel A^tb\parallel}$
      • 우변의 벡터의 Norm을 구해보면 1임을 알수 있다. 따라서 우변의 벡터는 Unit Vector이다. 좌변의 Symmetric Matrix의 경우 스칼라로 나누어 주어도 여전히 Symmetric Matrix이다.
      • 변형된 행렬과 벡터를 새로운 표기로 바꾸어 주자.
    • $A’x = b’$
      • 이때의 $A’$는 Symmetric Matrix이며 $b’$는 Unit Vector이다. 이 시스템의 근 x는 위의 일반식의 근과 일치한다.

이 경우 A는 Hermitian Matrix이기 때문에 Spectral Decomposition이 가능하다.

$A = \Gamma \Lambda \Gamma^t =: \sum_{j=1}^{r} \lambda_j \ket{u_j} \langle u_j \mid$

$\lambda_j ,\ket{u_j}$는 각각 A의 아이젠 밸류와 아이젠 벡터

이를 이용해 다음과 같은 Unitary Operator를 만들 수 있다.

$U_{A} = e^{2\pi i A} = \sum_{j=1}^{r}e^{2\pi i \lambda_j} \ket {u_j} \langle u_j\mid$ —– (주석의 1번 참고)

이렇게 Unitary Matrix 안에 들어간 $\lambda_j$는 어떤 값이되든 $\lambda’_j \in (0,1)$로 치환될 수 있다. —– (주석의 2번 참고)

따라서 A의 아이젠밸류를 0~1 사이의 값으로 가정할 수 있다. 이를 이진법으로 표현하면 다음과 같다.

$\lambda_j = 0.b_1b_2b_3…b_n \qquad b_j \in {0,1}$

이는 곧 m개의 bit를 이용하여 아이젠밸류를 근사추정한 것으로 해석할 수 있고 m이 늘어나면 늘어날수록 정확해 질 것이다.

만약 아이젠밸류가 무한소수가 아니라서 m개의 bit로 정확히 표현가능하다면 이를 아이젠밸류가 perfectly m-estimated된다고 정의하며 어떤 행렬의 아이젠밸류 전체가 m개의 bit로 표현가능할시 행렬이 perfectly m-estimated된다고 정의한다.

마지막으로 벡터 $\ket {b}$에 대해 A의 아이젠 벡터를 Basis로 삼아 표현해보자.

$\ket{b} = \sum_{j=1}^{r} a_j \ket{u_j}$

여기까지가 HHL Algorithm에 대한 사전 셋팅이다. 이제 본격적으로 HHL Algorithm에 대해서 알아보자.

HHL Algorithm

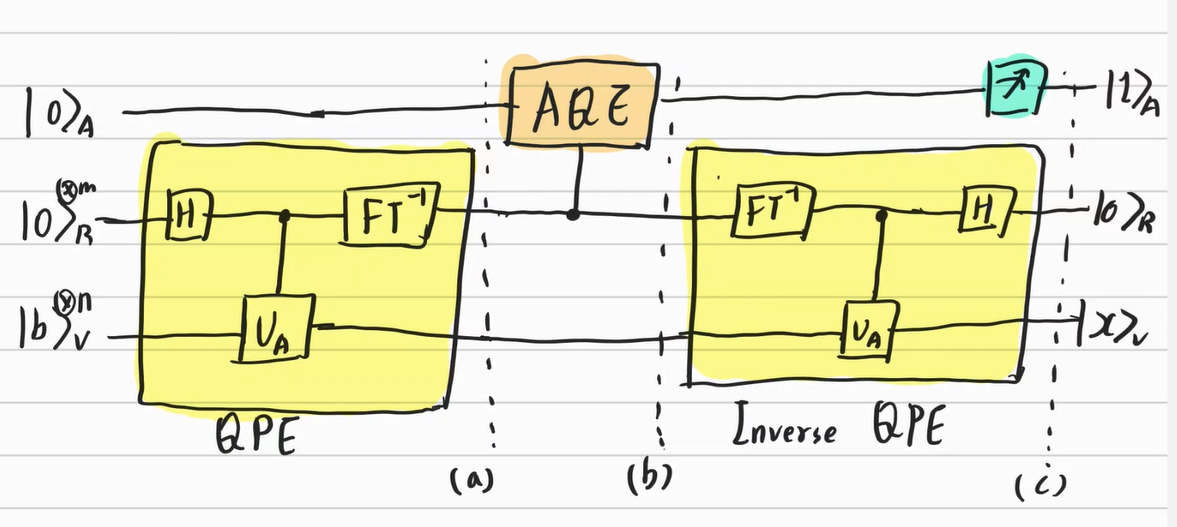
HHL Algorithm의 회로는 다음과 같다.

3. Additional Topic

위의 알고리즘에서는 뭔가 간질간질 거리는 부분들이 있을 수 있다. 이러한 내용들은 양자 컴퓨터의 알고리즘들이 아직 연구중에 있기 때문이다. 개중에 내가 공부하면서 어색함을 느낀 부분들과 비효율성을 느낀 부분들과 그에 대한 최신 연구 방향들에 대해서 몇가지 적어보려고 한다.

$U_{A}$와 $\ket{b}$의 차원에 대해서

위에서 보다시피 결과물 $\ket {x}$와 인풋값 $\ket{b}$는 큐빗의 상태 벡터로 이루어져 있다. 그런데 여러 개의 큐빗이 얽혀있는 상태로 표현되는 벡터는 2개 짜리 벡터의 텐서곱으로 이루어져 있기 때문에 무조건 차원이 $2^n$개로 이루어져 있다.

이 말인 즉슨, $\ket{x},\ket{b},U_{A}$ 모두 크기가 2,4,8,16 등 2의 배수로 제한이 되어있음을 의미한다. 설마해서 계속 살펴봤고 또 이것 때문에 계속 햇갈렸지만 A를 Unitary Matrix로 표현한 식을 보니 정말로 그렇게 되어 있었다.

물론 인풋값들의 사이즈가 고정되어 있어도 내가 구하고 싶은 A,b에 사이즈를 맞춰주기 위한 0벡터들을 집어넣어주면 되지만 그럼에도 많은 부작용이 발생할 것이다. 게다가 양자컴퓨터는 대용량처리를 위해 이용하는 만큼 천단위 만단위의 자료가 필요할 텐데, 1025 차원의 상태를 표현하기 위해 2048-1025=1023개의 불 필요한 상태를 집어넣어야하는 것은 비효율성이 느껴진다.

$U_{A}$의 실제 구현에 대해서

$U_A$는 행렬 A를 Unitary Matrix로 표현한 것으로 이론상 $U_{A} = e^{2\pi i A} $로 계산된다. 그러나 이 행렬을 구하는 것 자체가 어려운 일이다. $U_{A} = e^{2\pi i A} = \sum_{1}^{\infty} \frac{1}{k!}A^k$로 계산될 수 있으나 행렬을 수 없이 제곱해야 구할 수 있다는 점에서 계산이 오래걸릴 것이라는 것을 짐작할 수 있다.

이는 Matrix Exponential이라 하여 좀 더 빠르게 계산하는 것이 연구되고 있지만 아직은 A가 특정 조건을 만족할 때만 빠르게 계산할 수 있어 실용적이진 못하다.

따라서 이 문제와 위의 $\ket{b}$의 표현에 대한 문제까지 함께 해서 양자컴퓨터에서는 데이터를 큐빗으로 좀 더 효율적으로 표현하는 것에 대한 것이 연구의 한 축이기도 하다. 이를 Quantum Data Representation이라고 말한다. 이에 대해서도 계속 공부를 해 나가자.

AQE Part

AQE Part는 인풋 큐빗을 다음과 같이 바꾼다.

$\ket{0} \otimes \ket{\lambda_k}_R \rightarrow (\sqrt{1-\frac{c^2}{\lambda_k^2}}\ket{0}_A + \frac{c}{\lambda_k} \ket{1}_A) \otimes \ket{\lambda_k}_R$

즉, 하부의 인풋으로 들어온 아이젠밸류 추정치를 확률진폭의 가중치로 삼아 상부의 큐빗(Ancilla Qubit)을 변형(Encoding)하는 것이다. 이는 y 방향 회전 게이트($R_{Y}(\theta)$)를 통해서 수행할 수 있다.

그러나 $c = \frac{1}{\parallel A^{-1}b \parallel}$를 구하는 문제와 함께 양자컴퓨터의 알고리즘은 아직까지 효율적이라고 말하기 힘들다. 따라서 이 부분은 Classic Computer를 이용해서 계산한 다음 양자컴퓨터에서 다시 Inverse QPE로 계산하는 방식이 더 효율적이라고 말할 수 있다.

이것에 관한 알고리즘이 바로 Hybrid HHL Algorithm이다. ([HHL Algorithm For Quantum Linear Solver,Yonghae Lee1, Jaewoo Joo2,3 & Soojoon Lee (2019)])

아직까지는 이러한 방식으로 클래식 컴퓨터와 연계해서 계산하는 알고리즘들이 많이 필요하지 싶다. 관련한 공부를 계속 해보자.

proof and derivation

$U_{A} = e^{2\pi i A} = \sum_{j=1}^{r}e^{2\pi i \lambda_j} \ket {u_j} \langle u_j\mid$ —– (1)

pf)

$\exp(A)$는 해석적으로 다음과 같이 정의될 수 있다.

$\exp(A) = \sum_{k=0}^{\infty} \frac{1}{k!} A^k$

여1기에 A의 Spectral Decomposition Form을 활용하면 다음과 같이 적을 수 있다.

$\exp(2 \pi iA) = \sum_{k=0}^{\infty} \frac{(2 \pi i)^k}{k!} (\Gamma \Lambda \Gamma^t)^k = \sum_{k=0}^{\infty} \frac{(2 \pi i)^k}{k!} \Gamma \Lambda^k \Gamma $

​ $= \sum_{k=0}^{\infty} \frac{(2 \pi i)^k}{k!} \sum_{j=1}^{r} \lambda_j^k \ket{u_j} \langle u_j \mid$

​ $= \sum_{j=1}^{r} \ket{u_j} \langle u_j \mid \sum_{k=0}^{\infty} \frac{(2 \pi i \lambda_j)^k}{k!}$

​ $= \sum_{j=1}^{r} e^{2 \pi \lambda_j}\ket{u_j} \langle u_j \mid$

이렇게 Unitary Matrix 안에 들어간 $\lambda_j$는 어떤 값이되든 $\lambda’_j \in (0,1)$로 치환될 수 있다. —– (2)

pf)

$e^{2\pi i \lambda_j} = \cos(2 \pi \lambda_j) +i \sin( 2 \pi \lambda_j)$

(by Euler’s Fomula ; $e^{ix} = \cos(x) + i \sin(x)$ ; cos,sin,exp 함수의 해석적 정의로 유도할 수 있음)

​ $= f(\sin (2 \pi \lambda_j)) + i \sin (2\pi \lambda_j)$

​ $= g(\sin (2 \pi \lambda_j))$

​ $ = g(\sin (2\pi \lambda_j’))$

You May Also Enjoy